Section 13.2: Derivatives and Integrals of Vector Functions
Example
EXAMPLE 4 Show that if \(|\mathbf{r}(t)| = c\) (a constant), then \(\mathbf{r}'(t)\) is orthogonal to \(\mathbf{r}(t)\) for all t.
EXAMPLE 4 Show that if \(|\mathbf{r}(t)| = c\) (a constant), then \(\mathbf{r}'(t)\) is orthogonal to \(\mathbf{r}(t)\) for all t.
SOLUTION Since
\[ \mathbf{r}(t) \cdot \mathbf{r}(t) = |\mathbf{r}(t)|^2 = c^2 \] and \(c^2\) is a constant, Formula 4 of Theorem 3 gives \[ 0 = \frac{d}{dt}[\mathbf{r}(t) \cdot \mathbf{r}(t)] = \mathbf{r}'(t) \cdot \mathbf{r}(t) + \mathbf{r}(t) \cdot \mathbf{r}'(t) = 2\mathbf{r}'(t) \cdot \mathbf{r}(t) \] Thus \(\mathbf{r}'(t) \cdot \mathbf{r}(t) = 0\), which says that \(\mathbf{r}'(t)\) is orthogonal to \(\mathbf{r}(t)\).
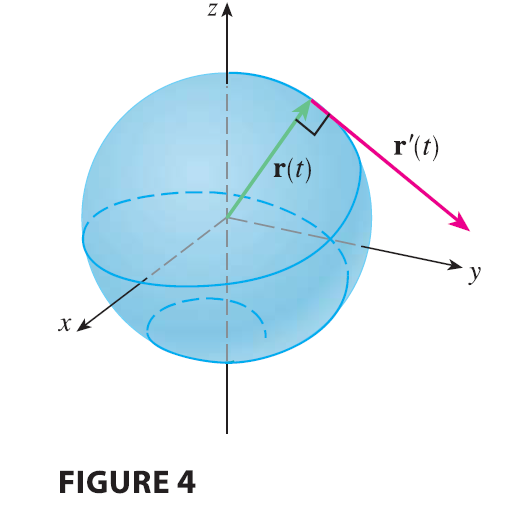
Geometrically, this result says that if a curve lies on a sphere with center the origin, then the tangent vector \(\mathbf{r}'(t)\) is always perpendicular to the position vector \(\mathbf{r}(t)\). (See Figure 4.)