Section 15.8: Triple Integration in Spherical Coordinates
Relationship between Spherical and Rectangular coordinates
The relationship between rectangular and spherical coordinates can be seen from Figure 5.
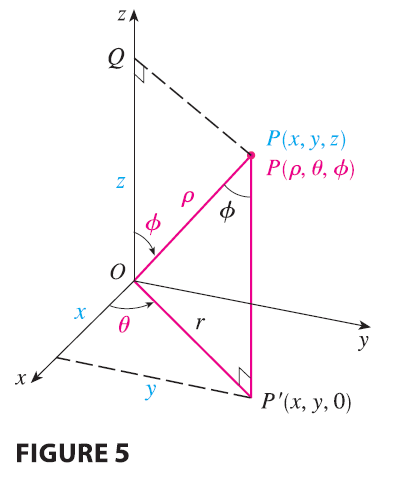
From triangles OPQ and OPP’ we have \[ z = \rho \cos \phi \qquad r = \rho \sin \phi \] But \(x = r \cos \theta\) and \(y = r \sin \theta\), so to convert from spherical to rectangular coordinates, we use the equations
\[ x = \rho \sin \phi \cos \theta \qquad y = \rho \sin \phi \sin \theta \qquad z = \rho \cos \phi \tag{1} \]
Also, the distance formula shows that
\[ \rho^2 = x^2 + y^2 + z^2 \tag{2} \]
We use this equation in converting from rectangular to spherical coordinates.
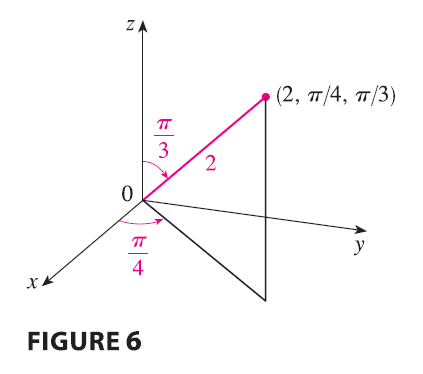
EXAMPLE 1 The point \((2, \pi/4, \pi/3)\) is given in spherical coordinates. Plot the point and find its rectangular coordinates.
EXAMPLE 2 The point \((0, 2\sqrt{3}, -2)\) is given in rectangular coordinates. Find spherical coordinates for this point.