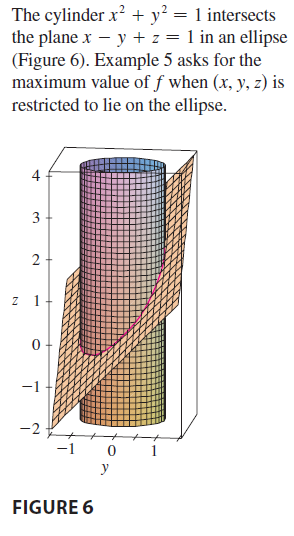
SOLUTION We maximize the function \(f(x, y, z) = x + 2y + 3z\) subject to the
constraints \(g(x, y, z) = x - y + z =
1\) and \(h(x, y, z) = x^2 + y^2 =
1\). The Lagrange condition is \(\nabla
f = \lambda \nabla g + \mu \nabla h\), so we solve the equations
\[
1 = \lambda + 2x\mu
\] \[
2 = -\lambda + 2y\mu
\] \[
3 = \lambda
\] \[
x - y + z = 1
\] \[
x^2 + y^2 = 1
\] Putting \(\lambda = 3\) [from
(19)] in (17), we get \(2x\mu = -2\),
so \(x = -1/\mu\). Similarly, (18)
gives \(y = 5/(2\mu)\). Substitution in
(21) then gives \[
\frac{1}{\mu^2} + \frac{25}{4\mu^2} = 1
\] and so \(\mu^2 = 29/4\),
\(\mu = \pm \sqrt{29}/2\). Then \(x = \mp 2/\sqrt{29}\), \(y = \pm 5/\sqrt{29}\), and, from (20),
\(z = 1 - x + y = 1 \mp (-2/\sqrt{29}) + (\pm
5/\sqrt{29}) = 1 \pm 7/\sqrt{29}\). The corresponding values of
\(f\) are \[
\left(\mp \frac{2}{\sqrt{29}}\right) + 2\left(\pm
\frac{5}{\sqrt{29}}\right) + 3\left(1 \pm \frac{7}{\sqrt{29}}\right) = 3
\pm \sqrt{29}
\] Therefore the maximum value of \(f\) on the given curve is \(3 + \sqrt{29}\).