Section 15.3: Integration in Polar Coordinates
Example
EXAMPLE 3 Use a double integral to find the area enclosed by one loop of the four-leaved rose \(r = \cos 2\theta\).
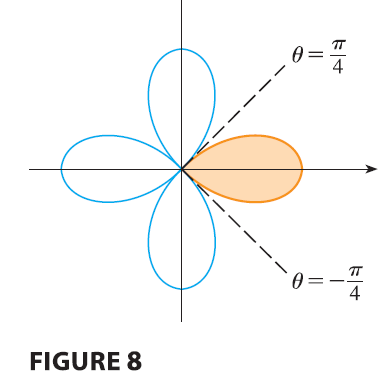
EXAMPLE 3 Use a double integral to find the area enclosed by one loop of the four-leaved rose \(r = \cos 2\theta\).

SOLUTION From the sketch of the curve in Figure 8, we see that a loop is given by the region \[ D = \{(r, \theta) | -\pi/4 \le \theta \le \pi/4, 0 \le r \le \cos 2\theta\} \] So the area is \[ A(D) = \iint_D dA = \int_{-\pi/4}^{\pi/4} \int_0^{\cos 2\theta} r dr d\theta = \int_{-\pi/4}^{\pi/4} \left[ \frac{r^2}{2} \right]_0^{\cos 2\theta} d\theta \] \[ = \frac{1}{2} \int_{-\pi/4}^{\pi/4} \cos^2 2\theta d\theta = \frac{1}{4} \int_{-\pi/4}^{\pi/4} (1 + \cos 4\theta) d\theta = \frac{1}{4} \left[ \theta + \frac{1}{4}\sin 4\theta \right]_{-\pi/4}^{\pi/4} = \frac{\pi}{8} \]