Section 14.1: Functions of Several Variables

Definition
The level curves of a function \(f\) of two variables are the curves with equations \(f(x, y) = k\), where \(k\) is a constant (in the range of \(f\)).

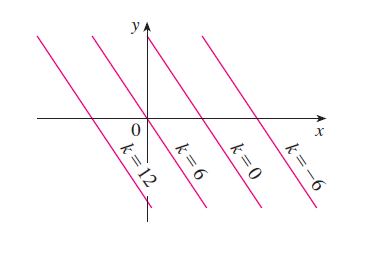
Example

Sketch the level curves of the function \(f(x, y) = 6 - 3x - 2y\) for the values \(k = -6, 0, 6, 12\).

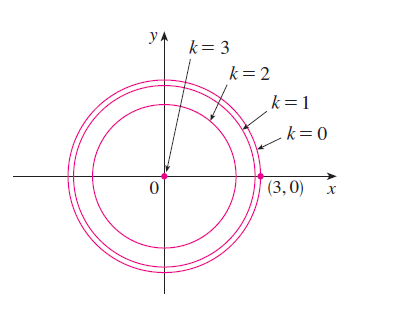
Example Level curves

Sketch the level curves for the function \[ g(x,y) = \sqrt{ 9 - x^2 - y^2} \qquad \text{for} \qquad k = 0, 1, 2, 3. \]

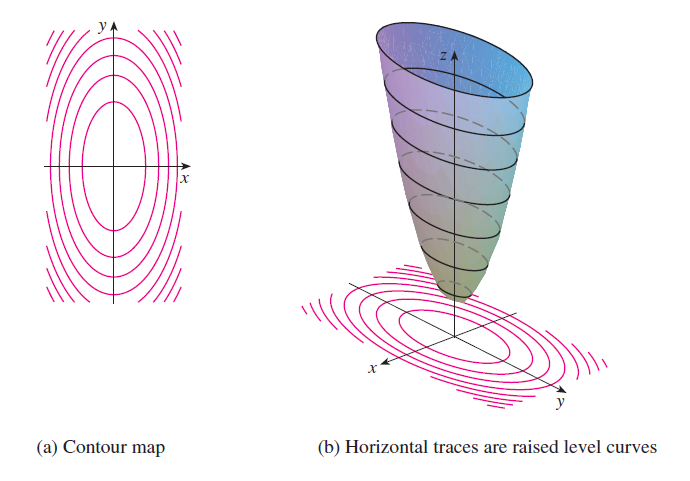
Example Level Curves

Sketch some level curves for the function \[ h(x,y) = 4x^2 + y^2 + 1 \]