Section 12.3: Dot Product

The dot product \(\mathbf{a} \cdot \mathbf{b}\) can be given a geometric interpretation in terms of the angle \(\theta\) between a and b, which is defined to be the angle between the representations of a and b that start at the origin, where \(0 \le \theta \le \pi\). In other words, \(\theta\) is the angle between the line segments \(\vec{OA}\) and \(\vec{OB}\) in Figure 1.

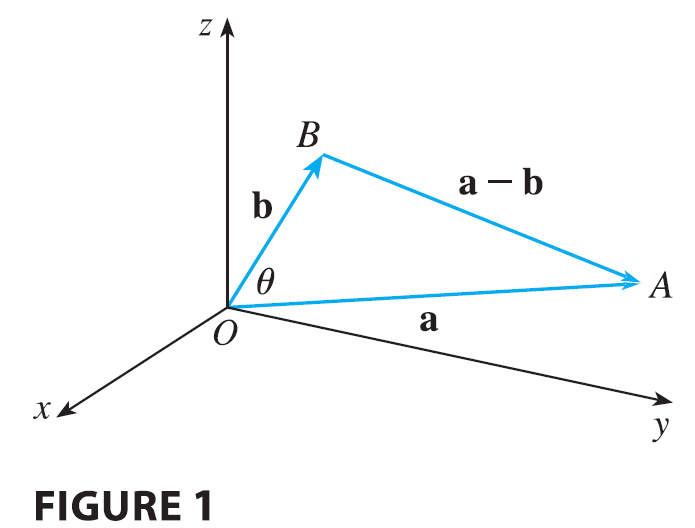
Note that if a and b are parallel vectors, then \(\theta = 0\) or \(\theta = \pi\).

The formula in the following theorem is used by physicists as the definition of the dot product.

Theorem 3 If \(\theta\) is the angle between the vectors a and b, then \[ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos\theta \]

PROOF If we apply the Law of Cosines to triangle OAB in Figure 1, we get \[ |\vec{AB}|^2 = |\vec{OA}|^2 + |\vec{OB}|^2 - 2|\vec{OA}||\vec{OB}|\cos\theta \tag{4} \] (Observe that the Law of Cosines still applies in the limiting cases when \(\theta = 0\) or \(\pi\), or \(\mathbf{a} = \mathbf{0}\) or \(\mathbf{b} = \mathbf{0}\).) But \(|\vec{OA}| = |\mathbf{a}|, |\vec{OB}| = |\mathbf{b}|\), and \(|\vec{AB}| = |\mathbf{a} - \mathbf{b}|\), so Equation 4 becomes \[ |\mathbf{a} - \mathbf{b}|^2 = |\mathbf{a}|^2 + |\mathbf{b}|^2 - 2|\mathbf{a}||\mathbf{b}|\cos\theta \tag{5} \] Using Properties 1, 2, and 3 of the dot product, we can rewrite the left side of this equation as follows: \[ |\mathbf{a} - \mathbf{b}|^2 = (\mathbf{a} - \mathbf{b}) \cdot (\mathbf{a} - \mathbf{b}) = \mathbf{a} \cdot \mathbf{a} - \mathbf{a} \cdot \mathbf{b} - \mathbf{b} \cdot \mathbf{a} + \mathbf{b} \cdot \mathbf{b} = |\mathbf{a}|^2 - 2\mathbf{a} \cdot \mathbf{b} + |\mathbf{b}|^2 \] Therefore Equation 5 gives \[ |\mathbf{a}|^2 - 2\mathbf{a} \cdot \mathbf{b} + |\mathbf{b}|^2 = |\mathbf{a}|^2 + |\mathbf{b}|^2 - 2|\mathbf{a}||\mathbf{b}|\cos\theta \] Thus \[ -2\mathbf{a} \cdot \mathbf{b} = -2|\mathbf{a}||\mathbf{b}|\cos\theta \] or \[ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos\theta \]

EXAMPLE 2 If the vectors a and b have lengths 4 and 6, and the angle between them is \(\pi/3\), find \(\mathbf{a} \cdot \mathbf{b}\).

EXAMPLE 3 Find the angle between the vectors \(\mathbf{a} = \langle 2, 2, -1 \rangle\) and \(\mathbf{b} = \langle 5, -3, 2 \rangle\).