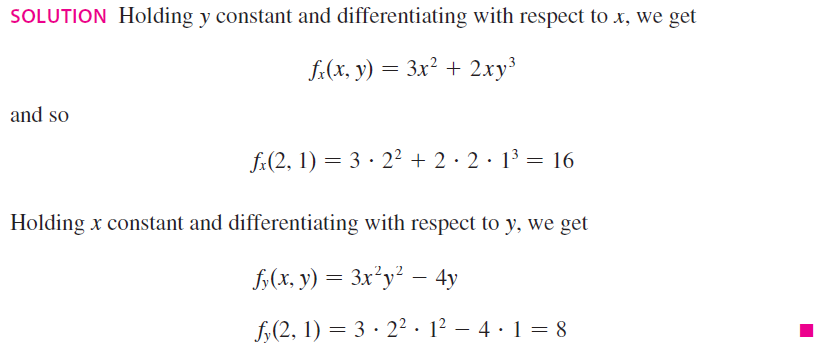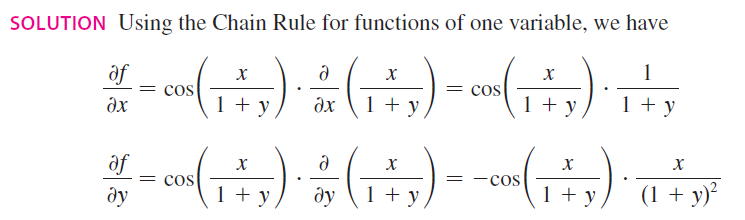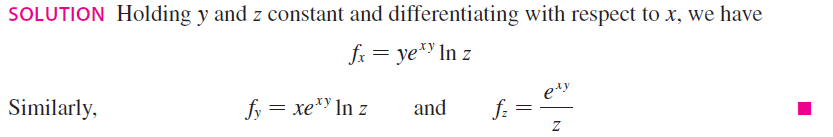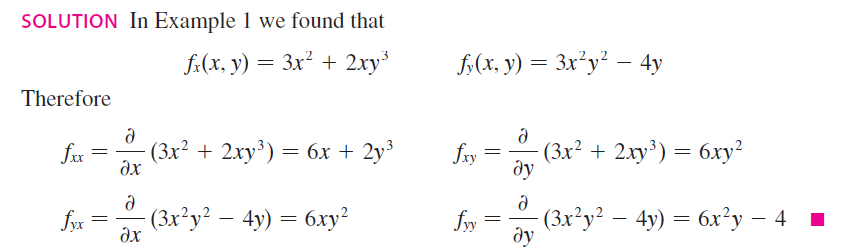Section 14.3 Partial Derivatives
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 14.3 Partial Derivatives |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 2:12 AM |
Table of contents
- Partial Derivatives
- Geomtric Interpretation of Partial Derivatives
- Chain rule inside partial derivatives
- Partial deriative of 3 or more variables.
- Higher Order Derivatives
- Is $f_{xy} = f_{yx}$?
- Partial Differential Equations
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5–8 Determine Signs of Partial Derivatives
- 9 Identify Surface Plots
- Ex: Contour Map Estimate
- Ex: Interpret Partial Derivatives as Slopes
- Ex: Interpret Partial Derivatives as Slopes
- Ex: 13–14 Compare Surface Plots of $f$, $f_x$, and $f_y$
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41-44: Find the indicated partial derivative
- Ex: 45–46. Use the definition of partial derivatives as limits (4) to find $f_x(x, y)$ and $f_y(x, y)$.
- Ex: 47–50: Use implicit differentiation to find $\partial z/\partial x$ and $\partial z/\partial y$.
- Ex 51–52: Find $\partial z/\partial x$ and $\partial z/\partial y$.
- Ex 63: Find the Indicated partial derivative
- Ex 64: Find the Indicated partial derivative
- Ex 65: Find the Indicated partial derivative
- Ex 66: Find the Indicated partial derivative
- Ex 67: Find the Indicated partial derivative
- Ex 68: Find the Indicated partial derivative
- Ex 69: Find the Indicated partial derivative
- Ex: 71
- Ex: 72
- Ex 73
- Ex 74
- Ex: 75
- Ex: 76
- Ex: 77
- Ex 78
- Ex 79
- Ex 80
- Ex 81
- Ex 82
- Ex 83
- Ex 84
- Ex 85
- Ex 86
- Ex 87
- Ex 88
- Ex 89
- Ex 90
- Ex 91
- Ex 92
- Ex 93
- Ex 94
- Ex 95
- Ex 96
- Ex 97
- Ex 98
- Ex 99
- Ex 100
- Ex 101
- Ex 102
- Ex 103
- Ex 104
- Ex 105
Partial Derivatives
Learning Outcomes - Definition and examples of partial derivatives
Rough Idea Differentiate the function with respect to one variable, treating other variables as constant.
Definition 
Example
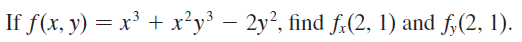
Geomtric Interpretation of Partial Derivatives
Question If derivatives in one variable functions were giving the slope of the tangent, what are we getting with partial derivatives in two variable or three variable functions?
Chain rule inside partial derivatives
Question 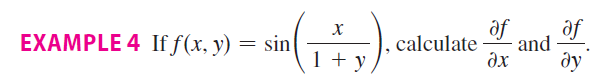
Question 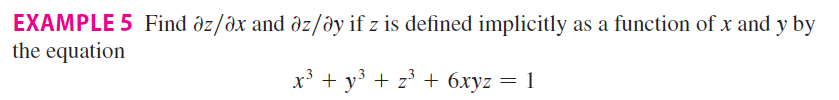
Partial deriative of 3 or more variables.
Basic idea is the same. Treat other variables as constant, and differentiate with respect to the variable of your interest.
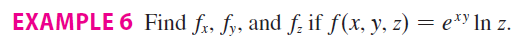
Higher Order Derivatives
| Second partial derivatives |
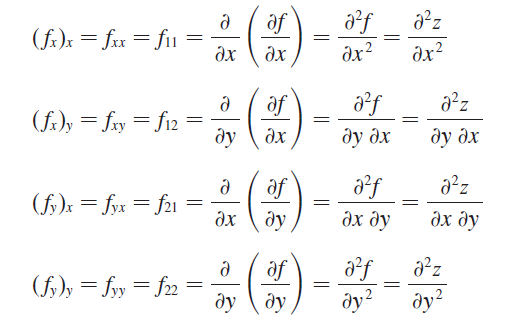 |
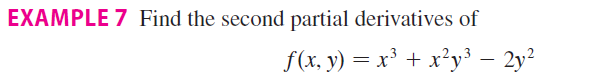
Is $f_{xy} = f_{yx}$?
Question: \(f_{xy} = f_{yx}\)? Mostly true in application but not always true.


Partial Differential Equations
Partial derivatives occur in partial differential equations that express certain physical laws.
Laplace Equation \[ \frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0 \] They play a role in problems of heat conduction, fluid flow, and electric potential.
| Example |
| Show that the function \(u(x, y) = e^x \sin y\) is a solution of Laplace’s equation. |
| \[ u_x = e^x \sin y \quad\quad u_y = e^x \cos y \] |
| \[ u_{xx} = e^x \sin y \quad\quad u_{yy} = -e^x \sin y \] |
| So |
| \[ u_{xx} + u_{yy} = e^x \sin y - e^x \sin y = 0 \] |
| Therefore \(u\) satisfies Laplace’s equation. |
The Wave Equation
\[ \frac{\partial^2 u}{\partial t^2} = a^2 \frac{\partial^2 u}{\partial x^2} \]
describes the motion of a waveform (a sound wave, a light wave, or a wave traveling along a vibrating string).
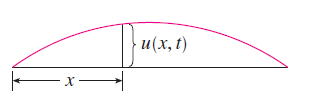
For instance, if \(u(x, t)\) represents the displacement of a vibrating violin string at time \(t\) and at a distance \(x\) from one end of the string, then \(u(x, t)\) satisfies the wave equation. Here the constant \(a\) depends on the density of the string and on the tension in the string.
Example
Verify that the function \(u(x, t) = \sin(x - at)\) satisfies the wave equation.
Exercise 1
The temperature \(T\) (in °C) at a location in the Northern Hemisphere depends on the longitude \(x\), latitude \(y\), and time \(t\), so we can write \(T = f(x, y, t)\). Let’s measure time in hours from the beginning of January.
What are the meanings of the partial derivatives \(\partial T/\partial x\), \(\partial T/\partial y\), and \(\partial T/\partial t\)?
Honolulu has longitude 158°W and latitude 21°N. Suppose that at 9:00 AM on January 1 the wind is blowing hot air to the northeast, so the air to the west and south is warm and the air to the north and east is cooler. Would you expect \(f_x(158, 21, 9)\), \(f_y(158, 21, 9)\), and \(f_t(158, 21, 9)\) to be positive or negative? Explain.
Exercise 2
At the beginning of this section we discussed the function \(I = f(T, H)\), where \(I\) is the heat index, \(T\) is the temperature, and \(H\) is the relative humidity. Use Table 1 to estimate \(f_T(92, 60)\) and \(f_H(92, 60)\). What are the practical interpretations of these values?
Exercise 3
The wind-chill index \(W\) is the perceived temperature when the actual temperature is \(T\) and the wind speed is \(v\), so we can write \(W = f(T, v)\). The following table of values is an excerpt from Table 1 in Section 14.1.
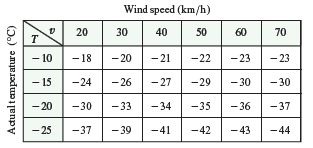
Estimate the values of \(f_T(-15, 30)\) and \(f_v(-15, 30)\). What are the practical interpretations of these values?
In general, what can you say about the signs of \(\partial W/\partial T\) and \(\partial W/\partial v\)?
What appears to be the value of the following limit?
\[ \lim_{v \to \infty} \frac{\partial W}{\partial v} \]
Exercise 4
The wave heights \(h\) in the open sea depend on the speed \(v\) of the wind and the length of time \(t\) that the wind has been blowing at that speed. Values of the function \(h = f(v, t)\) are recorded in feet in the following table.
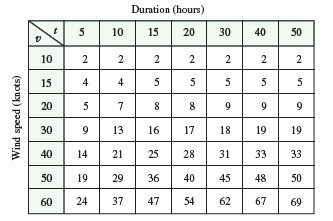 (a) What are the meanings of the partial
derivatives \(\partial h/\partial v\)
and \(\partial h/\partial t\)?
(a) What are the meanings of the partial
derivatives \(\partial h/\partial v\)
and \(\partial h/\partial t\)?
Estimate the values of \(f_t(40, 15)\) and \(f_t(40, 15)\). What are the practical interpretations of these values?
What appears to be the value of the following limit?
\[ \lim_{t \to \infty} \frac{\partial h}{\partial t} \]
Exercise 5–8 Determine Signs of Partial Derivatives
Determine the signs of the partial derivatives for the function \(f\) whose graph is shown.
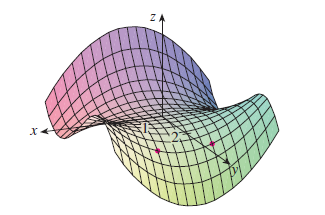
5.
(a) \(f_x(1, 2)\)
(b) \(f_y(1, 2)\)
6.
(a) \(f_x(-1, 2)\)
(b) \(f_y(-1, 2)\)
7.
(a) \(f_{xx}(-1, 2)\)
(b) \(f_{yy}(-1, 2)\)
8.
(a) \(f_{xy}(1, 2)\)
(b) \(f_{yx}(1, 2)\)
9 Identify Surface Plots
The following surfaces, labeled \(a\), \(b\), and \(c\), are graphs of a function \(f\) and its partial derivatives \(f_x\) and \(f_y\). Identify each surface and give
reasons for your choices. 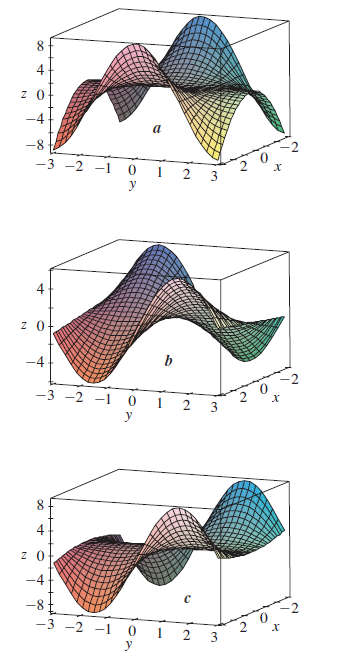
Ex: Contour Map Estimate
A contour map is given for a function \(f\). Use it to estimate \(f_x(2, 1)\) and \(f_y(2, 1)\). 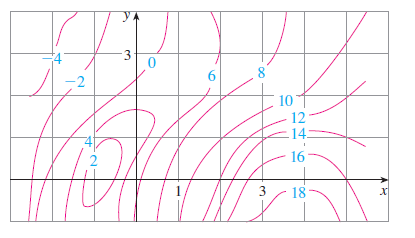
Ex: Interpret Partial Derivatives as Slopes
If \(f(x, y) = 16 - 4x^2 - y^2\), find \(f_x(1, 2)\) and \(f_y(1, 2)\) and interpret these numbers as slopes. Illustrate with either hand-drawn sketches or computer plots.
Ex: Interpret Partial Derivatives as Slopes
If \(f(x, y) = \sqrt{4 - x^2 - 4y^2}\), find \(f_x(1, 0)\) and \(f_y(1, 0)\) and interpret these numbers as slopes. Illustrate with either hand-drawn sketches or computer plots.
Ex: 13–14 Compare Surface Plots of $f$, $f_x$, and $f_y$
Find \(f\), \(f_x\), and \(f_y\) and graph \(f\), \(f_x\), and \(f_y\) with domains and viewpoints that enable you to see the relationships between them.
13. \(f(x, y) = x^2
y^3\)
14. \(f(x, y) = \dfrac{y}{1 +
x^2 y^2}\)
Exercise 15
Find the first partial derivatives of the function:
\[ f(x, y) = x^4 + 5x y^3 \]
Exercise 16
Find the first partial derivatives of the function:
\[ f(x, y) = x^2 y - 3y^4 \]
Exercise 17
Find the first partial derivatives of the function:
\[ f(x, t) = t^2 e^{-x} \]
Exercise 18
Find the first partial derivatives of the function:
\[ f(x, t) = \sqrt{3x + 4t} \]
Exercise 19
Find the first partial derivatives of the function:
\[ z = \ln(x + t^2) \]
Exercise 20
Find the first partial derivatives of the function:
\[ z = x \sin(xy) \]
Exercise 21
Find the first partial derivatives of the function:
\[ f(x, y) = \frac{x}{y} \]
Exercise 22
Find the first partial derivatives of the function:
\[ f(x, y) = \frac{x}{(x + y)^2} \]
Exercise 23
Find the first partial derivatives of the function:
\[ f(x, y) = \frac{a x + b y}{c x + d y} \]
Exercise 24
Find the first partial derivatives of the function:
\[ w = \frac{e^v}{u + v^2} \]
Exercise 25
Find the first partial derivatives of the function:
\[ g(u, v) = (u^2v - v^3)^5 \]
Exercise 26
Find the first partial derivatives of the function:
\[ u(r, \theta) = \sin(r \cos \theta) \]
Exercise 27
Find the first partial derivatives of the function:
\[ R(p, q) = \tan^{-1}(p q^2) \]
Exercise 28
Find the first partial derivatives of the function:
\[ f(x, y) = x^y \]
Exercise 29
Find the first partial derivatives of the function:
\[ F(x, y) = \int_y^x \cos(e^t) \, dt \]
Exercise 30
Find the first partial derivatives of the function:
\[ F(\alpha, \beta) = \int_\alpha^\beta \sqrt{t^3 + 1} \, dt \]
Exercise 31
Find the first partial derivatives of the function:
\[ f(x, y, z) = x^3 y z^2 + 2 y z \]
Exercise 32
Find the first partial derivatives of the function:
\[ f(x, y, z) = x y^2 e^{-x z} \]
Exercise 33
Find the first partial derivatives of the function:
\[ w = \ln(x + 2y + 3z) \]
Exercise 34
Find the first partial derivatives of the function:
\[ w = y \tan(x + 2z) \]
Exercise 35
Find the first partial derivatives of the function:
\[ p = \sqrt{t^4 + u^2 \cos v} \]
Exercise 36
Find the first partial derivatives of the function:
\[ u = x^{y/z} \]
Exercise 37
Find the first partial derivatives of the function:
\[ h(x, y, z, t) = x^2 y \cos(z/t) \]
Exercise 38
Find the first partial derivatives of the function:
\[ \Phi(x, y, z, t) = \frac{\alpha x + \beta y^2}{\gamma z + \delta t^2} \]
Exercise 39
Find the first partial derivatives of the function:
\[ u = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} \]
Exercise 40
Find the first partial derivatives of the function:
\[ u = \sin(x_1 + 2x_2 + \cdots + n x_n) \]
Exercise 41-44: Find the indicated partial derivative
41 \[ R(s,t) = t e^{\frac{s}{t}}, \qquad R_t (0,1) \]
42
\[f(x, y) = y \sin^{-1}(xy); \quad f_y(1, \tfrac{1}{2})\]
43
\[f(x, y, z) = \ln \left( \frac{1 - \sqrt{x^2 + y^2 + z^2}}{1 + \sqrt{x^2 + y^2 + z^2}} \right); \quad f_y(1, 2, 2)\]
44 \[f(x, y, z) = x^{yz}; \quad f_z(e, 1, 0)\]
Ex: 45–46. Use the definition of partial derivatives as limits (4) to find $f_x(x, y)$ and $f_y(x, y)$.
- \(f(x, y) = xy^2 - x^3 y\)
- \(f(x, y) = \frac{x}{x + y^2}\)
Ex: 47–50: Use implicit differentiation to find $\partial z/\partial x$ and $\partial z/\partial y$.
47
\[x^2 + 2y^2 + 3z^2 = 1\]
48 \[x^2 - y^2 + z^2 - 2z = 4\]
49 \[e^z = xyz\]
40 \[yz + x \ln y = z^2\]
Ex 51–52: Find $\partial z/\partial x$ and $\partial z/\partial y$.
51
- \(z = f(x) + g(y)\)
- \(z = f(x + y)\)
- \(z = f(xy)\)
52
(a) \(z = f(x)g(y)\)
(b) \(z = f(xy)\)
(c) \(z = f(x/y)\)
Ex 63: Find the Indicated partial derivative
\[f(x, y) = x^4 y^2 - x^3 y\]
Find: \(f_{xxx}\), \(f_{xyx}\)
Ex 64: Find the Indicated partial derivative
\[f(x, y) = \sin(2x + 5y)\]
Find: \(f_{xy}\)
Ex 65: Find the Indicated partial derivative
\[f(x, y, z) = e^{xyz^2}\]
Find: \(f_{xyz}\)
Ex 66: Find the Indicated partial derivative
\[g(r, s, t) = e^r \sin(st)\]
Find: \(g_{rst}\)
Ex 67: Find the Indicated partial derivative
\[W = \sqrt{u + v^2}\]
Find: \(\frac{\partial^3 W}{\partial u^2
\partial v}\)
Ex 68: Find the Indicated partial derivative
\[V = \ln(r + s^2 + t^3)\]
Find: \(\frac{\partial^3 V}{\partial r \,
\partial s \, \partial t}\)
Ex 69: Find the Indicated partial derivative
\[w = \frac{x}{y + 2z}\]
Find:
\(\frac{\partial^3 w}{\partial z \, \partial y
\, \partial x}\) and \(\frac{\partial^3
w}{\partial x^2 \, \partial y}\)
Ex: 71
\[f(x, y, z) = xy^2 z^3 +
\arcsin(x\sqrt{z})\]
Find: \(f_{xzy}\)
Hint: Which order of differentiation is easiest?
Ex: 72
\[g(x, y, z) = \sqrt{1 + xz} + \sqrt{1 -
xy}\]
Find: \(g_{xyz}\)
Hint: Use a different order of differentiation for each
term.
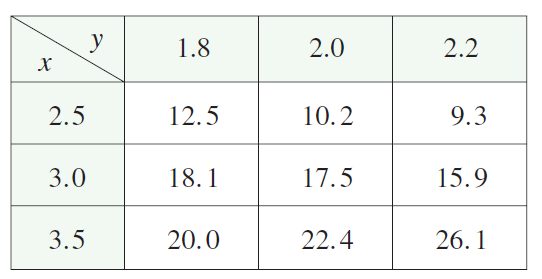
Ex 73
Use the table of values of \(f(x,
y)\) to estimate the values of
\(f_x(3, 2)\), \(f_x(3, 2.2)\), and \(f_{xy}(3, 2)\).
Ex 74
Level curves are shown for a function \(f\). Determine whether the following partial derivatives are positive or negative at the point \(P\).
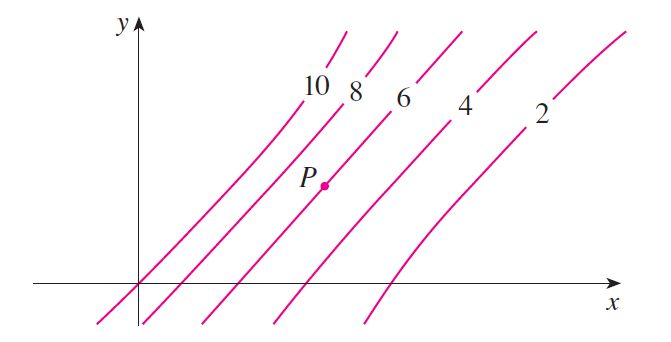
- \(f_x\)
- \(f_y\)
- \(f_{xx}\)
- \(f_{xy}\)
- \(f_{yy}\)
Ex: 75
Verify that the function
\[u = e^{-\alpha^2 k^2 t}
\sin(kx)\]
is a solution of the heat conduction equation
\[u_t = \alpha^2 u_{xx}.\]
Ex: 76
Determine whether each of the following functions is a solution of
Laplace’s equation
\[u_{xx} + u_{yy} = 0.\]
- \(u = x^2 + y^2\)
- \(u = \frac{x^2 - y^2}{x^2 +
y^2}\)
- \(u = x^3 + 3xy^2\)
- \(u = \ln \sqrt{x^2 + y^2}\)
- \(u = \sin x \cosh y + \cos x \sinh
y\)
- \(u = e^{-x} \cos y - e^{-y} \cos x\)
Ex: 77
Verify that the function
\[u = \frac{1}{\sqrt{x^2 + y^2 +
z^2}}\]
is a solution of the three-dimensional Laplace equation
\[u_{xx} + u_{yy} + u_{zz} = 0.\]
Ex 78
Show that each of the following functions is a solution of the wave
equation
\[u_{tt} = a^2 u_{xx}.\]
- \(u = \sin(kx)\sin(akt)\)
- \(u = \frac{t}{a^2 t^2 -
x^2}\)
- \(u = (x - at)^6 + (x +
at)^6\)
- \(u = \sin(x - at) + \ln(x + at)\)
Ex 79
If \(f\) and \(g\) are twice differentiable functions of a
single variable, show that the function
\[u(x, t) = f(x + at) + g(x -
at)\]
is a solution of the wave equation given in Exercise 78.
Ex 80
If
\[u = e^{a_1 x_1 + a_2 x_2 + \cdots + a_n
x_n},\]
where
\[a_1^2 + a_2^2 + \cdots + a_n^2 =
1,\]
show that
\[\frac{\partial^2 u}{\partial x_1^2} +
\frac{\partial^2 u}{\partial x_2^2} + \cdots + \frac{\partial^2
u}{\partial x_n^2} = u\]
Ex 81
The diffusion equation
\[\frac{\partial c}{\partial t} = D
\frac{\partial^2 c}{\partial x^2}\]
where \(D\) is a positive constant,
describes the diffusion of heat through a solid, or the concentration of
a pollutant at time \(t\) at a distance
\(x\) from the source of the pollution,
or the invasion of alien species into a new habitat.
Verify that the function
\[c(x, t) = \frac{1}{\sqrt{4\pi Dt}}
e^{-x^2/(4Dt)}\]
is a solution of the diffusion equation.
Ex 82
The temperature at a point \((x,
y)\) on a flat metal plate is given by
\[T(x, y) = \frac{60}{1 + x^2 +
y^2}\]
where \(T\) is measured in °C and \(x, y\) in meters.
Find the rate of change of temperature with respect to distance at
the point \((2, 1)\) in
(a) the \(x\)-direction
(b) the \(y\)-direction.
Ex 83
The total resistance \(R\) produced
by three conductors with resistances \(R_1,
R_2, R_3\) connected in a parallel electrical circuit is given by
the formula
\[\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}
+ \frac{1}{R_3}\]
Find \(\partial R / \partial R_1\).
Ex 84
Show that the Cobb-Douglas production function
\[P = bL^\alpha K^\beta\]
satisfies the equation
\[L \frac{\partial P}{\partial L} + K
\frac{\partial P}{\partial K} = (\alpha + \beta)P\]
Ex 85
Show that the Cobb-Douglas production function satisfies
\[P(L, K_0) = C_1(K_0)L^\alpha\]
by solving the differential equation
\[\frac{dP}{dL} = \alpha
\frac{P}{L}\]
(See Equation 6.)
Ex 86
Cobb and Douglas used the equation
\[P(L, K) =
1.01L^{0.75}K^{0.25}\]
to model the American economy from 1899 to 1922, where \(L\) is the amount of labor and \(K\) is the amount of capital.
- Calculate \(P_L\) and \(P_K\).
- Find the marginal productivity of labor and the marginal
productivity of capital in the year 1920, when \(L = 194\) and \(K
= 407\) (compared with the assigned values \(L = 100\) and \(K
= 100\) in 1899). Interpret the results.
- In the year 1920, which would have benefited production more, an increase in capital investment or an increase in spending on labor?
Ex 87
The van der Waals equation for \(n\) moles of a gas is
\[\left(P + \frac{n^2 a}{V^2} \right)(V - nb)
= nRT\]
where \(P\) is the pressure, \(V\) is the volume, and \(T\) is the temperature of the gas. The
constant \(R\) is the universal gas
constant and \(a\) and \(b\) are positive constants.
Calculate \(\partial T / \partial P\)
and \(\partial P / \partial V\).
Ex 88
The gas law for a fixed mass \(m\)
of an ideal gas at absolute temperature \(T\), pressure \(P\), and volume \(V\) is \(PV =
mRT\), where \(R\) is the gas
constant. Show that
\[\frac{\partial P}{\partial V}
\frac{\partial V}{\partial T} \frac{\partial T}{\partial P} =
-1\]
Ex 89
For the ideal gas of Exercise 88, show that
\[\frac{T}{\partial T} \frac{\partial
P}{\partial T} \frac{\partial V}{\partial T} = mR\]
Ex 90
The wind-chill index is modeled by the function
\[W = 13.12 + 0.6215T - 11.37v^{0.16} +
0.3965Tv^{0.16}\]
where \(T\) is the temperature (°C) and
\(v\) is the wind speed (km/h).
When \(T = -15^\circ\)C and \(v = 30\) km/h, by how much would you expect
the apparent temperature \(W\) to drop
if the actual temperature decreases by 1°C?
What if the wind speed increases by 1 km/h?
Ex 91
A model for the surface area of a human body is given by the
function
\[S = f(w, h) = 0.1091 w^{0.425}
h^{0.725}\]
where \(w\) is the weight (in pounds),
\(h\) is the height (in inches), and
\(S\) is in square feet. Calculate and
interpret the partial derivatives.
- \(\frac{\partial S}{\partial w}(160,
70)\)
- \(\frac{\partial S}{\partial h}(160, 70)\)
Ex 92
One of Poiseuille’s laws states that the resistance of blood flowing
through an artery is
\[R = C \frac{L}{r^4}\]
where \(L\) and \(r\) are the length and radius of the artery
and \(C\) is a positive constant
determined by the viscosity of the blood.
Calculate \(\partial R / \partial L\)
and \(\partial R / \partial r\) and
interpret them.
Ex 93
In the project on page 344 we expressed the power needed by a bird
during its flapping mode as
\[P(v, x, m) = Av^3 +
\frac{B(mg/x)^2}{v}\]
where \(A\) and \(B\) are constants, \(v\) is the velocity, \(m\) is the mass, and \(x\) is the fraction of the flying time
spent in flapping mode.
Calculate \(\partial P / \partial v\), \(\partial P / \partial x\), and \(\partial P / \partial m\) and interpret them.
Ex 94
The average energy \(E\) (in kcal)
needed for a lizard to walk or run a distance of 1 km has been modeled
by the equation
\[E(m, v) = 2.65m^{0.66} +
\frac{3.5m^{0.75}}{v}\]
where \(m\) is the body mass of the
lizard (in grams) and \(v\) is its
speed (in km/h).
Calculate \(E_m(400, 8)\) and \(E_v(400, 8)\) and interpret your
answers.
Source: C. Robbins, Wildlife Feeding and Nutrition, 2d
ed.
Ex 95
The kinetic energy of a body with mass \(m\) and velocity \(v\) is
\[K = \frac{1}{2}mv^2.\]
Show that
\[\frac{\partial K}{\partial m} \cdot
\frac{\partial^2 K}{\partial v^2} = K.\]
Ex 96
If \(a\), \(b\), \(c\) are the sides of a triangle and \(A\), \(B\), \(C\) are the opposite angles, find \(\partial A / \partial a\), \(\partial A / \partial b\), \(\partial A / \partial c\) by implicit differentiation of the Law of Cosines.
Ex 97
You are told that there is a function \(f\) whose partial derivatives are \(f_x(x, y) = x + 4y\) and \(f_y(x, y) = 3x - y\).
Should you believe it?
Ex 98
The paraboloid \(z = 6 - x - x^2 -
2y^2\) intersects the plane \(x =
1\) in a parabola.
Find parametric equations for the tangent line to this parabola at the
point \((1, 2, -4)\).
Use a computer to graph the paraboloid, the parabola, and the tangent
line on the same screen.
Ex 99
The ellipsoid \(4x^2 + 2y^2 + z^2 =
16\) intersects the plane \(y =
2\) in an ellipse.
Find parametric equations for the tangent line to this ellipse at the
point \((1, 2, 2)\).
Ex 100
In a study of frost penetration it was found that the temperature
\(T\) at time \(t\) (in days) at a depth \(x\) (in feet) can be modeled by the
function
\[T(x, t) = T_0 + T_1 e^{-\lambda x}
\sin(\omega t - \lambda x)\]
where \(\omega = 2\pi / 365\) and \(\lambda\) is a positive constant.
- Find \(\partial T / \partial x\).
What is its physical significance?
- Find \(\partial T / \partial t\).
What is its physical significance?
- Show that \(T\) satisfies the heat
equation \(T_t = k T_{xx}\) for a
certain constant \(k\).
- If \(\lambda = 0.2\), \(T_0 = 0\), and \(T_1 = 10\), use a computer to graph \(T(x, t)\).
- What is the physical significance of the term \(-\lambda x\) in the expression \(\sin(\omega t - \lambda x)\)?
Ex 101
Use Clairaut’s Theorem to show that if the third-order partial
derivatives of \(f\) are continuous,
then
\[f_{xyy} = f_{yxy} = f_{yyx}.\]
Ex 102
- How many \(n\)th-order partial
derivatives does a function of two variables have?
- If these partial derivatives are all continuous, how many of them
can be distinct?
- Answer the question in part (a) for a function of three variables.
Ex 103
If
\[f(x, y) = x(x^2 + y^2)^{-3/2} e^{\sin(x^2
y)}\]
find \(f_x(1, 0)\).
Hint: Instead of finding \(f_x(x,
y)\) first, note that it’s easier to use Equation 1 or Equation
2.
Ex 104
If \(f(x, y) = \sqrt[3]{x^3 + y^3}\), find \(f_x(0, 0)\).
Ex 105
Let
\[
f(x, y) =
\begin{cases}
\frac{x^3 y - x y^3}{x^2 + y^2}, & \text{if } (x, y) \ne (0, 0) \\
0, & \text{if } (x, y) = (0, 0)
\end{cases}
\]
- Use a computer to graph \(f\).
- Find \(f_x(x, y)\) and \(f_y(x, y)\) when \((x, y) \ne (0, 0)\).
- Find \(f_x(0, 0)\) and \(f_y(0, 0)\) using Equations 2 and 3.
- Show that \(f_{xy}(0, 0) = -1\) and
\(f_{yx}(0, 0) = 1\).
- Does the result of part (d) contradict Clairaut’s Theorem? Use graphs of \(f_{xy}\) and \(f_{yx}\) to illustrate your answer.