Section 14.4: Tangent Planes
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 14.4: Tangent Planes |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 3:57 AM |
Table of contents
- Learing Outcomes
- Tangent Plane
- Differentials
- Geometrical Interpretation of Differentials
- Example usage of differentials
- Differentials in 3 variables
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
Learing Outcomes
- Tangent Planes
- Linear Approximations
- Differentials
Tangent Plane
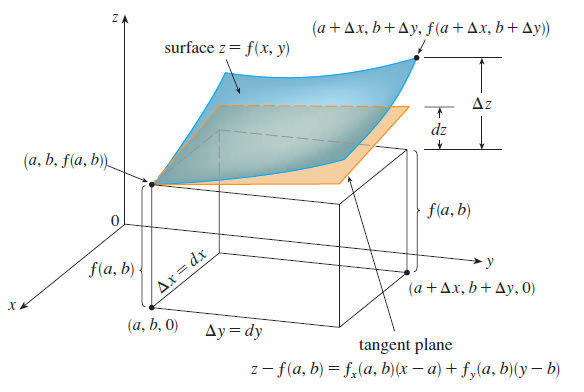
Suppose \(f\) has continuous partial derivatives. An equation of the tangent plane to the surface \(z = f(x, y)\) at the point \(P(x_0, y_0, z_0)\) is
\[ z - z_0 = f_x(x_0, y_0)(x - x_0) + f_y(x_0, y_0)(y - y_0) \]
EXAMPLE 1
Find the tangent plane to the elliptic paraboloid \(z = 2x^2 + y^2\) at the point \((1, 1, 3)\).
Differentials
If \(z = f(x,y)\), its differential is defined as
\[ dz = f_x(x, y)\,dx + f_y(x, y)\,dy = \frac{\partial z}{\partial x} dx + \frac{\partial z}{\partial y} dy \]
Geometrical Interpretation of Differentials
Example usage of differentials
EXAMPLE
(a) If \(z = f(x, y) = x^2 + 3xy -
y^2\), find the differential \(dz\).
(b) If \(x\) changes from 2 to 2.05 and
\(y\) changes from 3 to 2.96, compare
the values of \(\Delta z\) and \(dz\).
EXAMPLE
The base radius and height of a right circular cone are measured as 10
cm and 25 cm, respectively, with a possible error in measurement of as
much as 0.1 cm in each. Use differentials to estimate the maximum error
in the calculated volume of the cone.
Differentials in 3 variables
The differential \(dw\) is defined in terms of the differentials \(dx\), \(dy\), and \(dz\) of the independent variables by
\[ dw = \frac{\partial w}{\partial x} dx + \frac{\partial w}{\partial y} dy + \frac{\partial w}{\partial z} dz \]
EXAMPLE
The dimensions of a rectangular box are measured to be 75 cm, 60 cm, and
40 cm, and each measurement is correct to within 0.2 cm. Use
differentials to estimate the largest possible error when the volume of
the box is calculated from these measurements.
Exercise 1
Find an equation of the tangent plane to the given surface at the specified point.
\(z = 2x^2 + y^2 - 5y,\quad (1, 2, -4)\)
Exercise 2
Find an equation of the tangent plane to the given surface at the specified point.
\(z = (x + 2)^2 - 2(y - 1)^2 - 5,\quad (2, 3, 3)\)
Exercise 3
Find an equation of the tangent plane to the given surface at the specified point.
\(z = e^{x - y},\quad (2, 2, 1)\)
Exercise 4
Find an equation of the tangent plane to the given surface at the specified point. \(z = \dfrac{x}{y^2},\quad (-4, 2, -1)\)
Exercise 5
Find an equation of the tangent plane to the given surface at the specified point.
\(z = x \sin(x + y),\quad (-1, 1, 0)\)
Exercise 6
Find an equation of the tangent plane to the given surface at the specified point.
\(z = \ln(x - 2y),\quad (3, 1, 0)\)
Exercise 7
Graph the surface and the tangent plane at the given point. (Choose the domain and viewpoint so that you get a good view of both the surface and the tangent plane.) Then zoom in until the surface and the tangent plane become indistinguishable.
\(z = x^2 + xy + 3y^2,\quad (1, 1, 5)\)
Exercise 8
Graph the surface and the tangent plane at the given point. (Choose the domain and viewpoint so that you get a good view of both the surface and the tangent plane.) Then zoom in until the surface and the tangent plane become indistinguishable.
\(z = \sqrt{9 + x^2y^2},\quad (2, 2, 5)\)
Exercise 9
Draw the graph of \(f\) and its tangent plane at the given point. (Use your computer algebra system both to compute the partial derivatives and to graph the surface and its tangent plane.)
\(f(x, y) = \dfrac{1 + \cos^2(x - y)}{1 + \cos^2(x + y)},\quad \left(\dfrac{\pi}{3}, \dfrac{\pi}{6}, \dfrac{7}{4}\right)\)
Exercise 10
Draw the graph of \(f\) and its tangent plane at the given point. (Use your computer algebra system both to compute the partial derivatives and to graph the surface and its tangent plane.)
\(f(x, y) = e^{-xy/10}\left(\sqrt{x} + \sqrt{y} + \sqrt{xy}\right),\quad (1, 1, 3e^{-0.1})\)
Exercise 11
Explain why the function is differentiable at the given point. Then find the linearization \(L(x, y)\) of the function at that point.
\(f(x, y) = 1 + x \ln(xy - 5),\quad (2, 3)\)
Exercise 12
Explain why the function is differentiable at the given point. Then find the linearization \(L(x, y)\) of the function at that point.
\(f(x, y) = \sqrt{xy},\quad (1, 4)\)
Exercise 13
Explain why the function is differentiable at the given point. Then find the linearization \(L(x, y)\) of the function at that point.
\(f(x, y) = x^2 e^y,\quad (1, 0)\)
Exercise 14
Explain why the function is differentiable at the given point. Then find the linearization \(L(x, y)\) of the function at that point.
\(f(x, y) = \dfrac{1 + y}{1 + x},\quad (1, 3)\)
Exercise 15
Explain why the function is differentiable at the given point. Then find the linearization \(L(x, y)\) of the function at that point.
\(f(x, y) = 4 \arctan(xy),\quad (1, 1)\)
Exercise 16
Explain why the function is differentiable at the given point. Then find the linearization \(L(x, y)\) of the function at that point.
\(f(x, y) = y + \sin(x/y),\quad (0, 3)\)
Exercise 17
Verify the linear approximation at \((0, 0)\).
\(e^x \cos(xy) \approx x + 1\)
Exercise 18
Verify the linear approximation at \((0, 0)\).
\(\dfrac{y - 1}{x + 1} \approx x + y - 1\)
Exercise 19
Given that \(f\) is a differentiable function with \(f(2, 5) = 6\), \(f_x(2, 5) = 1\), and \(f_y(2, 5) = -1\), use a linear approximation to estimate \(f(2.2, 4.9)\).
Exercise 20
Find the linear approximation of the function
\[
f(x, y) = 1 - xy \cos \pi y \text{ at } (1, 1)
\]
and use it to approximate \(f(1.02,
0.97)\). Illustrate by graphing \(f\) and the tangent plane.
Exercise 21
Find the linear approximation of the function
\[
f(x, y, z) = \sqrt{x^2 + y^2 + z^2} \text{ at } (3, 2, 6)
\]
and use it to approximate the number \(\sqrt{(3.02)^2 + (1.97)^2 +
(5.99)^2}\).
Exercise 22
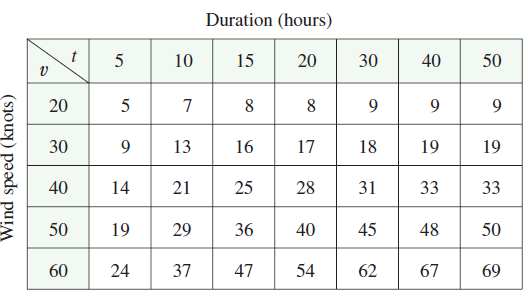
The wave heights \(h\) in the open sea depend on the speed \(v\) of the wind and the length of time \(t\) that the wind has been blowing at that speed. Values of the function \(h = f(v, t)\) are recorded in feet in the following table. Use the table to find a linear approximation to the wave height function when \(v\) is near 40 knots and \(t\) is near 20 hours. Then estimate the wave heights when the wind has been blowing for 24 hours at 43 knots.
Exercise 24
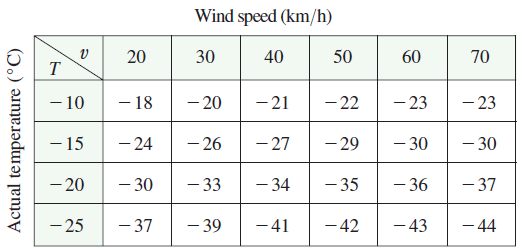
The wind-chill index \(W\) is the perceived temperature when the actual temperature is \(T\) and the wind speed is \(v\), so we can write \(W = f(T, v)\). The following table of values is an excerpt from Table 1 in Section 14.1. Use the table to find a linear approximation to the wind-chill index function when \(T\) is near \(-15^\circ\)C and \(v\) is near 50 km/h. Then estimate the wind chill index when the temperature is \(-17^\circ\)C and the wind speed is 55 km/h.
Exercise 25
Find the differential of the function
\[ z = e^{-2x} \cos(2\pi t) \]
Exercise 26
Find the differential of the function
\[
u = \sqrt{x^2 + 3y^2}
\]
Exercise 27
Find the differential of the function
\[
m = p^5 q^3
\]
Exercise 28
Find the differential of the function
\[
T = \dfrac{v}{1 + uvw}
\]
Exercise 29
Find the differential of the function
\[ R = \alpha \beta^2 \cos \gamma \]
Exercise 30
Find the differential of the function
\[ L = xze^{-y^2 - z^2} \]
Exercise 31
If \(z = 5x^2 + y^2\) and \((x, y)\) changes from \((1, 2)\) to \((1.05, 2.1)\), compare the values of \(\Delta z\) and \(dz\).
Exercise 32
If \(z = x^2 - xy + 3y^2\) and \((x, y)\) changes from \((3, -1)\) to \((2.96, -0.95)\), compare the values of \(\Delta z\) and \(dz\).
Exercise 33
The length and width of a rectangle are measured as 30 cm and 24 cm, respectively, with an error in measurement of at most 0.1 cm in each. Use differentials to estimate the maximum error in the calculated area of the rectangle.
Exercise 34
Use differentials to estimate the amount of metal in a closed cylindrical can that is 10 cm high and 4 cm in diameter if the metal in the top and bottom is 0.1 cm thick and the metal in the sides is 0.05 cm thick.
Exercise 35
Use differentials to estimate the amount of tin in a closed tin can with diameter 8 cm and height 12 cm if the tin is 0.04 cm thick.
Exercise 36
The wind-chill index is modeled by the function
\[
W = 13.12 + 0.6215T - 11.37v^{0.16} + 0.3965Tv^{0.16}
\]
where \(T\) is the temperature (in °C)
and \(v\) is the wind speed (in km/h).
The wind speed is measured as 26 km/h, with a possible error of \(\pm 2\) km/h, and the temperature is
measured as \(-11^\circ\)C, with a
possible error of \(\pm 1^\circ\)C. Use
differentials to estimate the maximum error in the calculated value of
\(W\) due to the measurement errors in
\(T\) and \(v\).
Exercise 37
The tension \(T\) in the string of
the yo-yo in the figure is
\[
T = \frac{mgR}{2r^2 + R^2}
\]
where \(m\) is the mass of the yo-yo
and \(g\) is acceleration due to
gravity. Use differentials to estimate the change in the tension if
\(R\) is increased from 3 cm to 3.1 cm
and \(r\) is increased from 0.7 cm to
0.8 cm. Does the tension increase or decrease?
Exercise 38
The pressure, volume, and temperature of a mole of an ideal gas are related by the equation \(PV = 8.31T\), where \(P\) is measured in kilopascals, \(V\) in liters, and \(T\) in kelvins. Use differentials to find the approximate change in the pressure if the volume increases from 12 L to 12.3 L and the temperature decreases from 310 K to 305 K.
Exercise 39
If \(R\) is the total resistance of
three resistors, connected in parallel, with resistances \(R_1\), \(R_2\), \(R_3\), then
\[
\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}
\]
If the resistances are measured in ohms as \(R_1 = 25\,\Omega\), \(R_2 = 40\,\Omega\), and \(R_3 = 50\,\Omega\), with a possible error
of 0.5% in each case, estimate the maximum error in the calculated value
of \(R\).
Exercise 40
A model for the surface area of a human body is given by
\[
S = 0.1091w^{0.425}h^{0.725}
\]
where \(w\) is the weight (in pounds),
\(h\) is the height (in inches), and
\(S\) is measured in square feet. If
the errors in measurement of \(w\) and
\(h\) are at most 2%, use differentials
to estimate the maximum percentage error in the calculated surface
area.
Exercise 41
In Exercise 14.1.39 and Example 14.3.3, the body mass index of a person was defined as \(B(m, h) = \frac{m}{h^2}\), where \(m\) is the mass in kilograms and \(h\) is the height in meters.
What is the linear approximation of \(B(m, h)\) for a child with mass 23 kg and height 1.10 m?
If the child’s mass increases by 1 kg and height by 3 cm, use the linear approximation to estimate the new BMI. Compare with the actual new BMI.
Exercise 42
Suppose you need to know an equation of the tangent plane to a
surface \(S\) at the point \(P(2, 1, 3)\). You don’t have an equation
for \(S\) but you know that the
curves
\[
\mathbf{r}_1(t) = \langle 2 + 3t,\ 1 - t^2,\ 3 - 4t + t^2 \rangle \\
\mathbf{r}_2(u) = \langle 1 + u^2,\ 2u^3 - 1,\ 2u + 1 \rangle
\]
both lie on \(S\). Find an equation of
the tangent plane at \(P\).
Exercise 43
Show that the function is differentiable by finding values of \(\varepsilon_1\) and \(\varepsilon_2\) that satisfy Definition 7.
\(f(x, y) = x^2 + y^2\)
Exercise 44
Show that the function is differentiable by finding values of \(\varepsilon_1\) and \(\varepsilon_2\) that satisfy Definition 7.
\(f(x, y) = xy - 5y^2\)
Exercise 45
Prove that if \(f\) is a function of two variables that is differentiable at \((a, b)\), then \(f\) is continuous at \((a, b)\).
Hint: Show that
\[
\lim_{(\Delta x, \Delta y) \to (0, 0)} f(a + \Delta x,\ b + \Delta y) =
f(a, b)
\]