Section 14.5 Chain Rule
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 14.5 Chain Rule |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 3:57 AM |
Table of contents
- Section Learning Outcomes
- The Chain Rule (Case 1)
- The Chain Rule (Case 2)
- Tree Diagram
- Example with Tree Diagram
- Example
- EXAMPLE
- Example
- Implicit Differentiation
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
- Exercise 49
- Exercise 50
- Exercise 51
- Exercise 52
- Exercise 53
- Exercise 54
- Exercise 55
- Exercise 56
- Exercise 57
- Exercise 58
- Exercise 59
Section Learning Outcomes
Chain Rule for multivariable functions
The Chain Rule (Case 1)
Suppose that \(z = f(x, y)\) is a differentiable function of \(x\) and \(y\), where \(x = g(t)\) and \(y = h(t)\) are both differentiable functions of \(t\). Then \(z\) is a differentiable function of \(t\) and \[ \frac{dz}{dt} = \frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt} \]
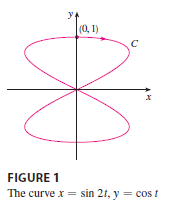
EXAMPLE 1 If \(z = x^2y + 3xy^4\), where \(x = \sin 2t\) and \(y = \cos t\), find \(dz/dt\) when \(t = 0\).
EXAMPLE 2 The pressure P (in kilopascals), volume V (in liters), and temperature T (in kelvins) of a mole of an ideal gas are related by the equation \(PV = 8.31T\). Find the rate at which the pressure is changing when the temperature is 300 K and increasing at a rate of 0.1 K/s and the volume is 100 L and increasing at a rate of 0.2 L/s.
The Chain Rule (Case 2)
Suppose that \(z = f(x, y)\) is a differentiable function of \(x\) and \(y\), where \(x = g(s, t)\) and \(y = h(s, t)\) are differentiable functions of \(s\) and \(t\). Then \[ \frac{\partial z}{\partial s} = \frac{\partial z}{\partial x} \frac{\partial x}{\partial s} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial s} \] \[ \frac{\partial z}{\partial t} = \frac{\partial z}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial t} \]
EXAMPLE 3 If \(z = e^x \sin y\), where \(x = st^2\) and \(y = s^2t\), find \(\partial z / \partial s\) and \(\partial z / \partial t\).
Tree Diagram
To remember the Chain Rule, it’s helpful to draw the tree diagram.
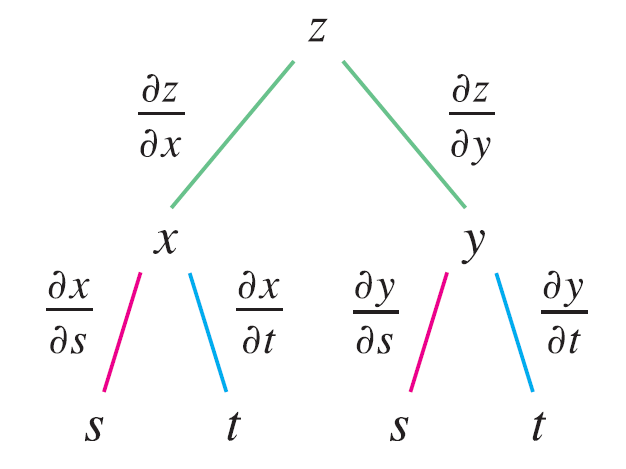
We draw branches from the dependent variable \(z\) to the intermediate variables \(x\) and \(y\) to indicate that \(z\) is a function of \(x\) and \(y\). Then we draw branches from \(x\) and \(y\) to the independent variables \(s\) and \(t\). On each branch we write the corresponding partial derivative. To find \(\partial z / \partial s\), we find the product of the partial derivatives along each path from \(z\) to \(s\) and then add these products: \[ \frac{\partial z}{\partial s} = \frac{\partial z}{\partial x} \frac{\partial x}{\partial s} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial s} \] Similarly, we find \(\partial z / \partial t\) by using the paths from \(z\) to \(t\).
Now we consider the general situation in which a dependent variable \(u\) is a function of \(n\) intermediate variables \(x_1, ..., x_n\), each of which is, in turn, a function of \(m\) independent variables \(t_1, ..., t_m\). Notice that there are \(n\) terms, one for each intermediate variable. The proof is similar to that of Case 1.
Example with Tree Diagram
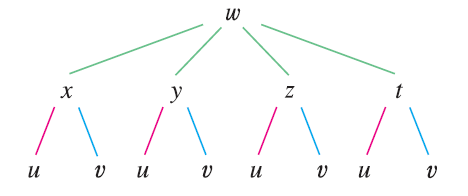
EXAMPLE 4 Write out the Chain Rule for the case where \(w = f(x, y, z, t)\) and \(x = x(u, v), y = y(u, v), z = z(u, v)\), and \(t = t(u, v)\).
Example
EXAMPLE 5 If \(u = x^4y + y^2z^3\), where \(x = rse^t, y = rs^2e^{-t}\), and \(z = r^2s \sin t\), find the value of \(\partial u / \partial s\) when \(r = 2, s = 1, t = 0\).
EXAMPLE
If \(g(s, t) = f(s^2 - t^2, t^2 - s^2)\) and \(f\) is differentiable, show that \(g\) satisfies the equation \[ t \frac{\partial g}{\partial s} + s \frac{\partial g}{\partial t} = 0 \]
Example
If \(z = f(x, y)\) has continuous second-order partial derivatives and \(x = r^2 + s^2\) and \(y = 2rs\), find (a) \(\partial z / \partial r\) and (b) \(\partial^2 z / \partial r^2\).
Implicit Differentiation
We suppose that an equation of the form \(F(x, y) = 0\) defines \(y\) implicitly as a differentiable function of \(x\), that is, \(y = f(x)\), where \(F(x, f(x)) = 0\) for all \(x\) in the domain of \(f\). If \(F\) is differentiable, we can apply Case 1 of the Chain Rule to differentiate both sides of the equation \(F(x, y) = 0\) with respect to \(x\). Since both \(x\) and \(y\) are functions of \(x\), we obtain \[ \frac{\partial F}{\partial x} \frac{dx}{dx} + \frac{\partial F}{\partial y} \frac{dy}{dx} = 0 \] But \(dx/dx = 1\), so if \(\partial F / \partial y \ne 0\) we solve for \(dy/dx\) and obtain \[ \frac{dy}{dx} = - \frac{\partial F / \partial x}{\partial F / \partial y} = - \frac{F_x}{F_y} \]
Note
To derive this equation we assumed that \(F(x, y) = 0\) defines \(y\) implicitly as a function of \(x\). The Implicit Function Theorem, proved in advanced calculus, gives conditions under which this assumption is valid: it states that if \(F\) is defined on a disk containing \((a, b)\), where \(F(a, b) = 0, F_y(a, b) \ne 0\), and \(F_x\) and \(F_y\) are continuous on the disk, then the equation \(F(x, y) = 0\) defines \(y\) as a function of \(x\) near the point \((a, b)\) and the derivative of this function is given by Equation 6.
EXAMPLE 8 Find \(y'\) if \(x^3 + y^3 = 6xy\).
Now we suppose that \(z\) is given implicitly as a function \(z = f(x, y)\) by an equation of the form \(F(x, y, z) = 0\). This means that \(F(x, y, f(x, y)) = 0\) for all \((x, y)\) in the domain of \(f\). If \(F\) and \(f\) are differentiable, then we can use the Chain Rule to differentiate the equation \(F(x, y, z) = 0\) as follows: \[ \frac{\partial F}{\partial x} \frac{\partial x}{\partial x} + \frac{\partial F}{\partial y} \frac{\partial y}{\partial x} + \frac{\partial F}{\partial z} \frac{\partial z}{\partial x} = 0 \] But \[ \frac{\partial}{\partial x}(x) = 1 \quad \text{and} \quad \frac{\partial}{\partial x}(y) = 0 \] so this equation becomes \[ \frac{\partial F}{\partial x} + \frac{\partial F}{\partial z} \frac{\partial z}{\partial x} = 0 \] If \(\partial F / \partial z \ne 0\), we solve for \(\partial z / \partial x\) and obtain the first formula in Equations 7. The formula for \(\partial z / \partial y\) is obtained in a similar manner. \[ \frac{\partial z}{\partial x} = - \frac{\partial F / \partial x}{\partial F / \partial z} \quad \frac{\partial z}{\partial y} = - \frac{\partial F / \partial y}{\partial F / \partial z} \]
Again, a version of the Implicit Function Theorem stipulates conditions under which our assumption is valid: if \(F\) is defined within a sphere containing \((a, b, c)\), where \(F(a, b, c) = 0, F_z(a, b, c) \ne 0\), and \(F_x, F_y\), and \(F_z\) are continuous inside the sphere, then the equation \(F(x, y, z) = 0\) defines \(z\) as a function of \(x\) and \(y\) near the point \((a, b, c)\) and this function is differentiable, with partial derivatives given by (7).
EXAMPLE 9 Find \(\frac{\partial z}{\partial x}\) and \(\frac{\partial z}{\partial y}\) if \(x^3 + y^3 + z^3 + 6xyz = 1\).
Exercise 1
Use chain rule to find \(\frac{dz}{dt}\) or \(\frac{dw}{dt}\).
\(z = x^2y^3 - x^2y\), \(x = t^2 + 1\), \(y = t^2 - 1\)
Exercise 2
Use chain rule to find \(\frac{dz}{dt}\) or \(\frac{dw}{dt}\).
\(z = \frac{x-y}{x+2y}\), \(x = e^t\), \(y = e^{-2t}\)
Exercise 3
Use chain rule to find \(\frac{dz}{dt}\) or \(\frac{dw}{dt}\).
\(z = \sin x \cos y\), \(x = \sqrt{t}\), \(y = 1/t\)
Exercise 4
Use chain rule to find \(\frac{dz}{dt}\) or \(\frac{dw}{dt}\).
\(z = \sqrt{1 + xy}\), \(x = \tan t\), \(y = \arctan t\)
Exercise 5
Use chain rule to find \(\frac{dz}{dt}\) or \(\frac{dw}{dt}\).
\(w = xe^{y/z}\), \(x = t^2\), \(y = 1-t\), \(z = 1 + 2t\)
Exercise 6
Use chain rule to find \(\frac{dz}{dt}\) or \(\frac{dw}{dt}\).
\(w = \ln \sqrt{x^2 + y^2 + z^2}\), \(x = \sin t\), \(y = \cos t\), \(z = \tan t\)
Exercise 7
Use chain rule to find \(\frac{ \partial z}{ \partial s}\) or \(\frac{ \partial z}{ \partial t}\).
\(z = (x - y)^5\), \(x = s^2t\), \(y = st^2\)
Exercise 8
Use chain rule to find \(\frac{ \partial z}{ \partial s}\) or \(\frac{ \partial z}{ \partial t}\).
\(z = \tan^{-1}(x^2 + y^2)\), \(x = s \ln t\), \(y = te^s\)
Exercise 9
Use chain rule to find \(\frac{ \partial z}{ \partial s}\) or \(\frac{ \partial z}{ \partial t}\).
\(z = \ln(3x + 2y)\), \(x = s \sin t\), \(y = t \cos s\)
Exercise 10
Use chain rule to find \(\frac{ \partial z}{ \partial s}\) or \(\frac{ \partial z}{ \partial t}\).
\(z = \sqrt{x}e^{xy}\), \(x = 1 + st\), \(y = s^2 - t^2\)
Exercise 11
Use chain rule to find \(\frac{ \partial z}{ \partial s}\) or \(\frac{ \partial z}{ \partial t}\).
\(z = e^r \cos \theta\), \(r = st\), \(\theta = \sqrt{s^2 + t^2}\)
Exercise 12
Use chain rule to find \(\frac{ \partial z}{ \partial s}\) or \(\frac{ \partial z}{ \partial t}\).
\(z = \tan(u/v)\), \(u = 2s + 3t\), \(v = 3s - 2t\)
Exercise 13
Let \(p(t) = f(g(t), h(t))\), where \(f\) is differentiable, \(g(2) = 4\), \(g'(2) = -3\), \(h(2) = 5\), \(h'(2) = 6\), \(f_x(4, 5) = 2\), \(f_y(4, 5) = 8\). Find \(p'(2)\).
Exercise 14
Let \(R(s, t) = G(u(s, t), v(s, t))\), where \(G\), \(u\), and \(v\) are differentiable, \(u(1, 2) = 5\), \(u_s(1, 2) = 4\), \(u_t(1, 2) = -3\), \(v(1, 2) = 7\), \(v_s(1, 2) = 2\), \(v_t(1, 2) = 6\), \(G_u(5, 7) = 9\), \(G_v(5, 7) = -2\). Find \(R_s(1, 2)\) and \(R_t(1, 2)\).
Exercise 15
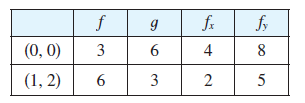
Suppose \(f\) is a differentiable function of \(x\) and \(y\), and \(g(u, v) = f(e^u + \sin v, e^u + \cos v)\). Use the table of values to calculate \(g_u(0, 0)\) and \(g_v(0, 0)\).
Exercise 16
Suppose \(f\) is a differentiable function of \(x\) and \(y\), and \(g(r, s) = f(2r - s, s^2 - 4r)\). Use the table of values in Exercise 15 to calculate \(g_r(1, 2)\) and \(g_s(1, 2)\).
Exercise 17
Use a tree diagram to write out the Chain Rule for the given case. Assume all functions are differentiable. \(u = f(x, y)\), where \(x = x(r, s, t)\), \(y = y(r, s, t)\)
Exercise 18
Use a tree diagram to write out the Chain Rule for the given case. Assume all functions are differentiable. \(w = f(x, y, z)\), where \(x = x(u, v)\), \(y = y(u, v)\), \(z = z(u, v)\)
Exercise 19
Use a tree diagram to write out the Chain Rule for the given case. Assume all functions are differentiable. \(T = F(p, q, r)\), where \(p = p(x, y, z)\), \(q = q(x, y, z)\), \(r = r(x, y, z)\)
Exercise 20
Use a tree diagram to write out the Chain Rule for the given case. Assume all functions are differentiable. \(R = F(t, u)\) where \(t = t(w, x, y, z)\), \(u = u(w, x, y, z)\)
Exercise 21
Use the Chain Rule to find the indicated partial derivatives. \(z = x^4 + x^2y\), \(x = s + 2t - u\), \(y = stu^2\); find \(\frac{\partial z}{\partial s}\), \(\frac{\partial z}{\partial t}\), \(\frac{\partial z}{\partial u}\) when \(s = 4, t = 2, u = 1\).
Exercise 22
Use the Chain Rule to find the indicated partial derivatives. \(T = \frac{v}{2u+v}\), \(u = p q \sqrt{r}\), \(v = p \sqrt{q} r\); find \(\frac{\partial T}{\partial p}\), \(\frac{\partial T}{\partial q}\), \(\frac{\partial T}{\partial r}\) when \(p = 2, q = 1, r = 4\).
Exercise 23
Use the Chain Rule to find the indicated partial derivatives. \(w = xy + yz + zx\), \(x = r \cos \theta\), \(y = r \sin \theta\), \(z = r\theta\); find \(\frac{\partial w}{\partial r}\), \(\frac{\partial w}{\partial \theta}\) when \(r = 2, \theta = \pi/2\).
Exercise 24
Use the Chain Rule to find the indicated partial derivatives. \(P = \sqrt{u^2 + v^2 + w^2}\), \(u = xe^y\), \(v = ye^x\), \(w = e^{xy}\); find \(\frac{\partial P}{\partial x}\), \(\frac{\partial P}{\partial y}\) when \(x = 0, y = 2\).
Exercise 25
Use the Chain Rule to find the indicated partial derivatives. \(N = \frac{p+q}{p+r}\), \(p = u + vw\), \(q = v + uw\), \(r = w + uv\); find \(\frac{\partial N}{\partial u}\), \(\frac{\partial N}{\partial v}\), \(\frac{\partial N}{\partial w}\) when \(u = 2, v = 3, w = 4\).
Exercise 26
Use the Chain Rule to find the indicated partial derivatives. \(u = x^2e^{y\tau}\), \(x = \alpha^2\beta\), \(y = \beta^2\gamma\), \(\tau = \gamma^2\alpha\); find \(\frac{\partial u}{\partial \alpha}\), \(\frac{\partial u}{\partial \beta}\), \(\frac{\partial u}{\partial \gamma}\) when \(\alpha = -1, \beta = 2, \gamma = 1\).
Exercise 27
Use Equation 6 to find \(dy/dx\). \(y \cos x = x^2 + y^2\)
Exercise 28
Find \(dy/dx\). \(\cos(xy) = 1 + \sin y\)
Exercise 29
Find \(dy/dx\). \(\tan^{-1}(x^2y) = x + xy^2\)
Exercise 30
Find \(dy/dx\). \(e^y \sin x = x + xy\)
Exercise 31
Find \(\partial z/\partial x\) and \(\partial z/\partial y\). \(x^2 + 2y^2 + 3z^2 = 1\)
Exercise 32
Find \(\partial z/\partial x\) and \(\partial z/\partial y\). \(x^2 - y^2 + z^2 - 2z = 4\)
Exercise 33
Find \(\partial z/\partial x\) and \(\partial z/\partial y\). \(e^z = xyz\)
Exercise 34
Find \(\partial z/\partial x\) and \(\partial z/\partial y\). \(yz + x \ln y = z^2\)
Exercise 35
The temperature at a point \((x, y)\) is \(T(x, y)\), measured in degrees Celsius. A bug crawls so that its position after \(t\) seconds is given by \(x = \sqrt{1 + t}\), \(y = 2 + \frac{1}{3}t\), where \(x\) and \(y\) are measured in centimeters. The temperature function satisfies \(T_x(2, 3) = 4\) and \(T_y(2, 3) = 3\). How fast is the temperature rising on the bug’s path after 3 seconds?
Exercise 36
Wheat production \(W\) in a given year depends on the average temperature \(T\) and the annual rainfall \(R\). Scientists estimate that the average temperature is rising at a rate of 0.15°C/year and rainfall is decreasing at a rate of 0.1 cm/year. They also estimate that at current production levels, \(\partial W / \partial T = -2\) and \(\partial W / \partial R = 8\). (a) What is the significance of the signs of these partial derivatives? (b) Estimate the current rate of change of wheat production, \(dW/dt\).
Exercise 37
The speed of sound traveling through ocean water with salinity 35 parts per thousand has been modeled by the equation \(C = 1449.2 + 4.6T - 0.055T^2 + 0.00029T^3 + 0.016D\) where \(C\) is the speed of sound (in meters per second), \(T\) is the temperature (in degrees Celsius), and \(D\) is the depth below the ocean surface (in meters). A scuba diver began a leisurely dive into the ocean water; the diver’s depth and the surrounding water temperature over time are recorded in the following graphs. Estimate the rate of change (with respect to time) of the speed of sound through the ocean water experienced by the diver 20 minutes into the dive. What are the units?
Exercise 38
The radius of a right circular cone is increasing at a rate of 1.8 in/s while its height is decreasing at a rate of 2.5 in/s. At what rate is the volume of the cone changing when the radius is 120 in. and the height is 140 in.?
Exercise 39
The length \(l\), width \(w\), and height \(h\) of a box change with time. At a certain instant the dimensions are \(l = 1\) m and \(w = h = 2\) m, and \(l\) and \(w\) are increasing at a rate of 2 m/s while \(h\) is decreasing at a rate of 3 m/s. At that instant find the rates at which the following quantities are changing. (a) The volume (b) The surface area (c) The length of a diagonal
Exercise 40
The voltage \(V\) in a simple electrical circuit is slowly decreasing as the battery wears out. The resistance \(R\) is slowly increasing as the resistor heats up. Use Ohm’s Law, \(V = IR\), to find how the current \(I\) is changing at the moment when \(R = 400\ \Omega\), \(I = 0.08\) A, \(dV/dt = -0.01\) V/s, and \(dR/dt = 0.03\ \Omega\)/s.
Exercise 41
The pressure of 1 mole of an ideal gas is increasing at a rate of 0.05 kPa/s and the temperature is increasing at a rate of 0.15 K/s. Use the equation \(PV = 8.31T\) in Example 2 to find the rate of change of the volume when the pressure is 20 kPa and the temperature is 320 K.
Exercise 42
A manufacturer has modeled its yearly production function \(P\) (the value of its entire production, in millions of dollars) as a Cobb-Douglas function \(P(L, K) = 1.47L^{0.65}K^{0.35}\) where \(L\) is the number of labor hours (in thousands) and \(K\) is the invested capital (in millions of dollars). Suppose that when \(L = 30\) and \(K = 8\), the labor force is decreasing at a rate of 2000 labor hours per year and capital is increasing at a rate of $500,000 per year. Find the rate of change of production.
Exercise 43
One side of a triangle is increasing at a rate of 3 cm/s and a second side is decreasing at a rate of 2 cm/s. If the area of the triangle remains constant, at what rate does the angle between the sides change when the first side is 20 cm long, the second side is 30 cm, and the angle is \(\pi/6\)?
Exercise 44
A sound with frequency \(f_s\) is produced by a source traveling along a line with speed \(v_s\). If an observer is traveling with speed \(v_o\) along the same line from the opposite direction toward the source, then the frequency of the sound heard by the observer is \(f_o = \left(\frac{c + v_o}{c - v_s}\right) f_s\) where \(c\) is the speed of sound, about 332 m/s. (This is the Doppler effect.) Suppose that, at a particular moment, you are in a train traveling at 34 m/s and accelerating at 1.2 m/s\(^2\). A train is approaching you from the opposite direction on the other track at 40 m/s, accelerating at 1.4 m/s\(^2\), and sounds its whistle, which has a frequency of 460 Hz. At that instant, what is the perceived frequency that you hear and how fast is it changing?
Exercise 45
Assume that all the given functions are differentiable. If \(z = f(x, y)\), where \(x = r \cos \theta\) and \(y = r \sin \theta\), (a) find \(\partial z/\partial r\) and \(\partial z/\partial \theta\) and (b) show that \[ \left(\frac{\partial z}{\partial x}\right)^2 + \left(\frac{\partial z}{\partial y}\right)^2 = \left(\frac{\partial z}{\partial r}\right)^2 + \frac{1}{r^2}\left(\frac{\partial z}{\partial \theta}\right)^2 \]
Exercise 46
Assume that all the given functions are differentiable. If \(u = f(x, y)\), where \(x = e^s \cos t\) and \(y = e^s \sin t\), show that \[ \left(\frac{\partial u}{\partial x}\right)^2 + \left(\frac{\partial u}{\partial y}\right)^2 = e^{-2s}\left[\left(\frac{\partial u}{\partial s}\right)^2 + \left(\frac{\partial u}{\partial t}\right)^2\right] \]
Exercise 47
Assume that all the given functions are differentiable. If \(z = \frac{1}{x}[f(x - y) + g(x + y)]\), show that \[ \frac{\partial}{\partial x}\left(x^2 \frac{\partial z}{\partial x}\right) = x^2 \frac{\partial^2 z}{\partial y^2} \]
Exercise 48
Assume that all the given functions are differentiable. If \(z = \frac{1}{y}[f(ax + y) + g(ax - y)]\), show that \[ \frac{\partial}{\partial x}\left(y^2 \frac{\partial z}{\partial x}\right) = a^2 \frac{\partial}{\partial y}\left(y^2 \frac{\partial z}{\partial y}\right) \]
Exercise 49
Assume that all the given functions have continuous second-order partial derivatives. Show that any function of the form \(z = f(x + at) + g(x - at)\) is a solution of the wave equation \[ \frac{\partial^2 z}{\partial t^2} = a^2 \frac{\partial^2 z}{\partial x^2} \] [Hint: Let \(u = x + at, v = x - at\).]
Exercise 50
Assume that all the given functions have continuous second-order partial derivatives. If \(u = f(x, y)\), where \(x = e^s \cos t\) and \(y = e^s \sin t\), show that \[ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = e^{-2s}\left[\frac{\partial^2 u}{\partial s^2} + \frac{\partial^2 u}{\partial t^2}\right] \]
Exercise 51
Assume that all the given functions have continuous second-order partial derivatives. If \(z = f(x, y)\), where \(x = r^2 + s^2\) and \(y = 2rs\), find \(\partial^2 z/\partial r \partial s\). (Compare with Example 7.)
Exercise 52
Assume that all the given functions have continuous second-order partial derivatives. If \(z = f(x, y)\), where \(x = r \cos \theta\) and \(y = r \sin \theta\), find (a) \(\partial z/\partial r\), (b) \(\partial z/\partial \theta\), and (c) \(\partial^2 z/\partial r \partial \theta\).
Exercise 53
Assume that all the given functions have continuous second-order partial derivatives. If \(z = f(x, y)\), where \(x = r \cos \theta\) and \(y = r \sin \theta\), show that \[ \frac{\partial^2 z}{\partial x^2} + \frac{\partial^2 z}{\partial y^2} = \frac{\partial^2 z}{\partial r^2} + \frac{1}{r^2}\frac{\partial^2 z}{\partial \theta^2} + \frac{1}{r}\frac{\partial z}{\partial r} \]
Exercise 54
Assume that all the given functions have continuous second-order partial derivatives. Suppose \(z = f(x, y)\), where \(x = g(s, t)\) and \(y = h(s, t)\). (a) Show that \[ \frac{\partial^2 z}{\partial t^2} = \frac{\partial^2 z}{\partial x^2}\left(\frac{\partial x}{\partial t}\right)^2 + 2\frac{\partial^2 z}{\partial x \partial y}\frac{\partial x}{\partial t}\frac{\partial y}{\partial t} + \frac{\partial^2 z}{\partial y^2}\left(\frac{\partial y}{\partial t}\right)^2 + \frac{\partial z}{\partial x}\frac{\partial^2 x}{\partial t^2} + \frac{\partial z}{\partial y}\frac{\partial^2 y}{\partial t^2} \] (b) Find a similar formula for \(\partial^2 z/\partial s \partial t\).
Exercise 55
A function \(f\) is called homogeneous of degree n if it satisfies the equation \(f(tx, ty) = t^n f(x, y)\) for all \(t\), where \(n\) is a positive integer and \(f\) has continuous second-order partial derivatives. (a) Verify that \(f(x, y) = x^2y + 2xy^2 + 5y^3\) is homogeneous of degree 3. (b) Show that if \(f\) is homogeneous of degree \(n\), then \[ x \frac{\partial f}{\partial x} + y \frac{\partial f}{\partial y} = nf(x, y) \] [Hint: Use the Chain Rule to differentiate \(f(tx, ty)\) with respect to \(t\).]
Exercise 56
If \(f\) is homogeneous of degree \(n\), show that \[ x^2 \frac{\partial^2 f}{\partial x^2} + 2xy \frac{\partial^2 f}{\partial x \partial y} + y^2 \frac{\partial^2 f}{\partial y^2} = n(n-1)f(x, y) \]
Exercise 57
If \(f\) is homogeneous of degree \(n\), show that \(f_x(tx, ty) = t^{n-1}f_x(x, y)\)
Exercise 58
Suppose that the equation \(F(x, y, z) = 0\) implicitly defines each of the three variables \(x, y\), and \(z\) as functions of the other two: \(z = f(x, y)\), \(y = g(x, z)\), \(x = h(y, z)\). If \(F\) is differentiable and \(F_x, F_y\), and \(F_z\) are all nonzero, show that \[ \frac{\partial z}{\partial x} \frac{\partial x}{\partial y} \frac{\partial y}{\partial z} = -1 \]
Exercise 59
Equation 6 is a formula for the derivative \(dy/dx\) of a function defined implicitly by an equation \(F(x, y) = 0\), provided that \(F\) is differentiable and \(F_y \ne 0\). Prove that if \(F\) has continuous second derivatives, then a formula for the second derivative of \(y\) is \[ \frac{d^2 y}{dx^2} = - \frac{F_{xx}F_y^2 - 2F_{xy}F_x F_y + F_{yy}F_x^2}{F_y^3} \]