Section 14.6: Directional Derivatives & Gradient Vector
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 14.6: Directional Derivatives & Gradient Vector |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 2:32 AM |
Table of contents
- Section Learning Outcomes
- Directional Derivatives
- The Gradient Vector
- Gradients and Directional derivatives for functions of Three Variables
- Importance of Gradients: Maximizing the Directional Derivative
- Tangent Planes to Level Surfaces
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
- Exercise 49
- Exercise 50
- Exercise 51
- Exercise 52
- Exercise 53
- Exercise 54
- Exercise 55
- Exercise 56
- Exercise 57
- Exercise 58
- Exercise 59
- Exercise 60
- Exercise 61
- Exercise 62
- Exercise 63
- Exercise 64
- Exercise 65
- Exercise 66
- Exercise 67
- Exercise 68
- Exercise 69
- Exercise 70
Section Learning Outcomes
- Directional Derivatives
- Gradient Vectors
Directional Derivatives
Recall that if \(z = f(x, y)\), then the partial derivatives \(f_x\) and \(f_y\) are defined as
\(f_x(x_0, y_0) = \lim_{h\to0} \frac{f(x_0 + h, y_0) - f(x_0, y_0)}{h}\)
\(f_y(x_0, y_0) = \lim_{h\to0} \frac{f(x_0, y_0 + h) - f(x_0, y_0)}{h}\)
and represent the rates of change of \(z\) in the x- and y-directions, that is, in the directions of the unit vectors i and j.
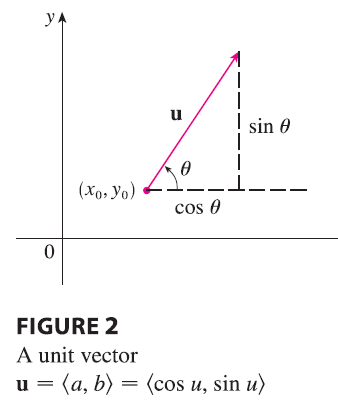
Suppose that we now wish to find the rate of change of \(z\) at \((x_0, y_0)\) in the direction of an arbitrary unit vector \(\mathbf{u} = \langle a, b \rangle\). To do this we consider the surface S with the equation \(z = f(x, y)\) (the graph of f) and we let \(z_0 = f(x_0, y_0)\).
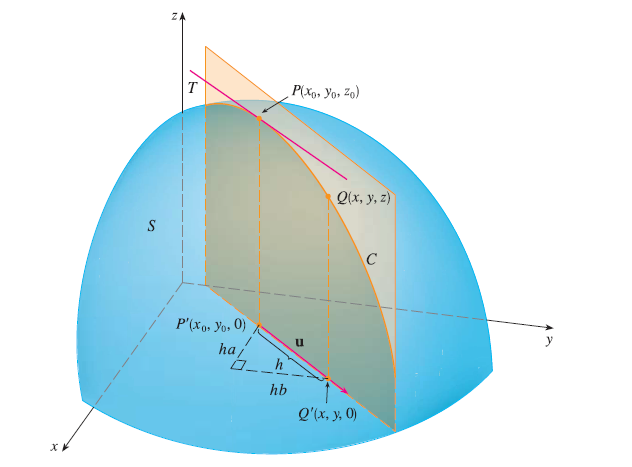
Then the point \(P(x_0, y_0, z_0)\) lies on S. The vertical plane that passes through P in the direction of u intersects S in a curve C. The slope of the tangent line T to C at the point P is the rate of change of z in the direction of u.
If \(Q(x, y, z)\) is another point on C and P’, Q’ are the projections of P, Q onto the xy-plane, then the vector \(\vec{P'Q'}\) is parallel to u and so
\(\vec{P'Q'} = h\mathbf{u} = \langle ha, hb \rangle\)
for some scalar h. Therefore \(x - x_0 = ha\), \(y - y_0 = hb\), so \(x = x_0 + ha\), \(y = y_0 + hb\), and
\(\frac{\Delta z}{h} = \frac{z - z_0}{h} = \frac{f(x_0 + ha, y_0 + hb) - f(x_0, y_0)}{h}\)
If we take the limit as \(h \to 0\), we obtain the rate of change of z (with respect to distance) in the direction of u, which is called the directional derivative of f in the direction of u.
Definition The directional derivative of \(f\) at \((x_0, y_0)\) in the direction of a unit vector \(\mathbf{u} = \langle a, b \rangle\) is
\(D_{\mathbf{u}}f(x_0, y_0) = \lim_{h\to0} \frac{f(x_0 + ha, y_0 + hb) - f(x_0, y_0)}{h}\)
if this limit exists.
Theorem If f is a differentiable function of x and y, then f has a directional derivative in the direction of any unit vector \(\mathbf{u} = \langle a, b \rangle\) and
\[ D_{\mathbf{u}}f(x, y) = f_x(x, y)a + f_y(x, y)b \]
PROOF If we define a function g of the single variable h by
\(g(h) = f(x_0 + ha, y_0 + hb)\)
then, by the definition of a derivative, we have
\(g'(0) = \lim_{h\to0} \frac{g(h) - g(0)}{h} = \lim_{h\to0} \frac{f(x_0 + ha, y_0 + hb) - f(x_0, y_0)}{h} = D_{\mathbf{u}}f(x_0, y_0)\)
On the other hand, we can write \(g(h) = f(x, y)\), where \(x = x_0 + ha\), \(y = y_0 + hb\), so the Chain Rule gives
\(g'(h) = \frac{\partial f}{\partial x}\frac{dx}{dh} + \frac{\partial f}{\partial y}\frac{dy}{dh} = f_x(x, y)a + f_y(x, y)b\)
If we now put \(h=0\), then \(x = x_0\), \(y = y_0\), and
\(g'(0) = f_x(x_0, y_0)a + f_y(x_0, y_0)b\)
Comparing the equations for \(g'(0)\), we see that
\(D_{\mathbf{u}}f(x_0, y_0) = f_x(x_0, y_0)a + f_y(x_0, y_0)b\)
If the unit vector u makes an angle \(\theta\) with the positive x-axis, then we can write \(\mathbf{u} = \langle \cos\theta, \sin\theta \rangle\) and the formula in Theorem 3 becomes
\(D_{\mathbf{u}}f(x, y) = f_x(x, y)\cos\theta + f_y(x, y)\sin\theta\)
EXAMPLE Find the directional derivative \(D_{\mathbf{u}}f(x, y)\) if
\(f(x, y) = x^3 - 3xy + 4y^2\)
and u is the unit vector given by angle \(\theta = \pi/6\). What is \(D_{\mathbf{u}}f(1, 2)\)?
The Gradient Vector
Definition If f is a function of two variables x and y, then the gradient of f is the vector function \(\nabla f\) defined by
\[ \nabla f(x, y) = \langle f_x(x, y), f_y(x, y) \rangle = \frac{\partial f}{\partial x}\mathbf{i} + \frac{\partial f}{\partial y}\mathbf{j} \]
EXAMPLE If \(f(x, y) = \sin x + e^{xy}\), then
\(\nabla f(x, y) = \langle f_x, f_y \rangle = \langle \cos x + ye^{xy}, xe^{xy} \rangle\)
and
\(\nabla f(0, 1) = \langle 2, 0 \rangle\)
With this notation for the gradient vector, we can rewrite the equation for the directional derivative of a differentiable function as
\[ D_{\mathbf{u}}f(x, y) = \nabla f(x, y) \cdot \mathbf{u} \]
This expresses the directional derivative in the direction of a unit vector u as the scalar projection of the gradient vector onto u.
EXAMPLE Find the directional derivative of the function \(f(x, y) = x^2y^3 - 4y\) at the point \((2, -1)\) in the direction of the vector \(\mathbf{v} = 2\mathbf{i} + 5\mathbf{j}\).
Gradients and Directional derivatives for functions of Three Variables
For functions of three variables we can define directional derivatives in a similar manner. Again \(D_{\mathbf{u}}f(x, y, z)\) can be interpreted as the rate of change of the function in the direction of a unit vector u.
Definition The directional derivative of f at \((x_0, y_0, z_0)\) in the direction of a unit vector \(\mathbf{u} = \langle a, b, c \rangle\) is
\(D_{\mathbf{u}}f(x_0, y_0, z_0) = \lim_{h\to0} \frac{f(x_0 + ha, y_0 + hb, z_0 + hc) - f(x_0, y_0, z_0)}{h}\)
if this limit exists.
Gradients
For a function f of three variables, the gradient vector, denoted by \(\nabla f\) or grad f, is
\[ \nabla f = \langle f_x, f_y, f_z \rangle = \frac{\partial f}{\partial x}\mathbf{i} + \frac{\partial f}{\partial y}\mathbf{j} + \frac{\partial f}{\partial z}\mathbf{k} \]
Then, just as with functions of two variables, the formula for the directional derivative can be rewritten as
\[ D_{\mathbf{u}}f(x, y, z) = \nabla f(x, y, z) \cdot \mathbf{u} \]
EXAMPLE If \(f(x, y, z) = x \sin(yz)\), (a) find the gradient of f and (b) find the directional derivative of f at \((1, 3, 0)\) in the direction of \(\mathbf{v} = \mathbf{i} + 2\mathbf{j} - \mathbf{k}\).
Importance of Gradients: Maximizing the Directional Derivative
Suppose we have a function f of two or three variables and we consider all possible directional derivatives of f at a given point. These give the rates of change of f in all possible directions. We can then ask the questions: in which of these directions does f change fastest and what is the maximum rate of change? The answers are provided by the following theorem.
Theorem Suppose f is a differentiable function of two or three variables. The maximum value of the directional derivative \(D_{\mathbf{u}}f(\mathbf{x})\) is \(|\nabla f(\mathbf{x})|\) and it occurs when u has the same direction as the gradient vector \(\nabla f(\mathbf{x})\).
PROOF From the equations we have
\(D_{\mathbf{u}}f = \nabla f \cdot \mathbf{u} = |\nabla f||\mathbf{u}|\cos\theta = |\nabla f|\cos\theta\)
where \(\theta\) is the angle between \(\nabla f\) and u. The maximum value of \(\cos\theta\) is 1 and this occurs when \(\theta = 0\). Therefore the maximum value of \(D_{\mathbf{u}}f\) is \(|\nabla f|\) and it occurs when \(\theta = 0\), that is, when u has the same direction as \(\nabla f\).
EXAMPLE (a) If \(f(x, y) = xe^y\), find the rate of change of f at the point P(2, 0) in the direction from P to Q(1/2, 2). (b) In what direction does f have the maximum rate of change? What is this maximum rate of change?
EXAMPLE 7 Suppose that the temperature at a point (x, y, z) in space is given by \(T(x, y, z) = 80/(1 + x^2 + 2y^2 + 3z^2)\), where T is measured in degrees Celsius and x, y, z in meters. In which direction does the temperature increase fastest at the point (1, 1, -2)? What is the maximum rate of increase?
Tangent Planes to Level Surfaces
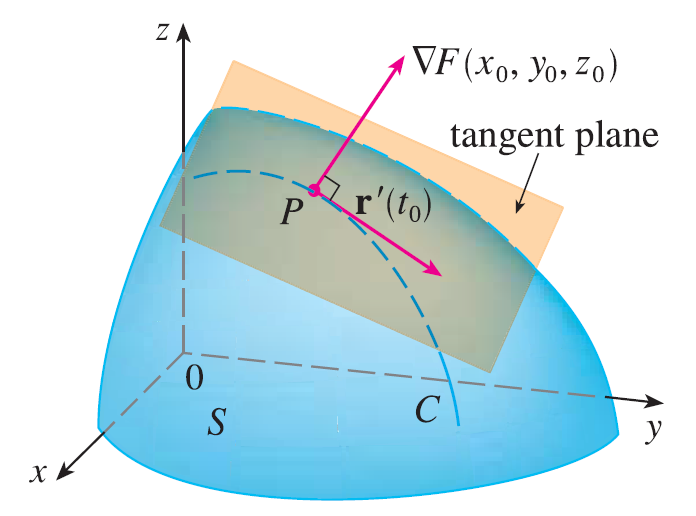
Suppose S is a surface with equation \(F(x, y, z) = k\), that is, it is a level surface of a function F of three variables, and let \(P(x_0, y_0, z_0)\) be a point on S. Let C be any curve that lies on the surface S and passes through the point P. The curve C is described by a continuous vector function \(\mathbf{r}(t) = \langle x(t), y(t), z(t) \rangle\). Let \(t_0\) be the parameter value corresponding to P; that is, \(\mathbf{r}(t_0) = \langle x_0, y_0, z_0 \rangle\). Since C lies on S, any point \((x(t), y(t), z(t))\) must satisfy the equation of S, that is,
\(F(x(t), y(t), z(t)) = k\)
If x, y, and z are differentiable functions of t and F is also differentiable, then we can use the Chain Rule to differentiate both sides of the equation as follows:
\(\frac{\partial F}{\partial x}\frac{dx}{dt} + \frac{\partial F}{\partial y}\frac{dy}{dt} + \frac{\partial F}{\partial z}\frac{dz}{dt} = 0\)
But, since \(\nabla F = \langle F_x, F_y, F_z \rangle\) and \(\mathbf{r}'(t) = \langle x'(t), y'(t), z'(t) \rangle\), the equation can be written in terms of a dot product as
\(\nabla F \cdot \mathbf{r}'(t) = 0\)
In particular, when \(t = t_0\) we have \(\mathbf{r}(t_0) = \langle x_0, y_0, z_0 \rangle\), so
\(\nabla F(x_0, y_0, z_0) \cdot \mathbf{r}'(t_0) = 0\)
This equation says that the gradient vector at P, \(\nabla F(x_0, y_0, z_0)\), is perpendicular to the tangent vector \(\mathbf{r}'(t_0)\) to any curve C on S that passes through P. If \(\nabla F(x_0, y_0, z_0) \neq \mathbf{0}\), it is therefore natural to define the tangent plane to the level surface \(F(x, y, z) = k\) at \(P(x_0, y_0, z_0)\) as the plane that passes through P and has normal vector \(\nabla F(x_0, y_0, z_0)\). Using the standard equation of a plane, we can write the equation of this tangent plane as
\(F_x(x_0, y_0, z_0)(x - x_0) + F_y(x_0, y_0, z_0)(y - y_0) + F_z(x_0, y_0, z_0)(z - z_0) = 0\)
The normal line to S at P is the line passing through P and perpendicular to the tangent plane. The direction of the normal line is therefore given by the gradient vector \(\nabla F(x_0, y_0, z_0)\) and so, its symmetric equations are
\(\frac{x - x_0}{F_x(x_0, y_0, z_0)} = \frac{y - y_0}{F_y(x_0, y_0, z_0)} = \frac{z - z_0}{F_z(x_0, y_0, z_0)}\)
In the special case in which the equation of a surface S is of the form \(z = f(x, y)\), we can rewrite the equation as
\(F(x, y, z) = f(x, y) - z = 0\)
and regard S as a level surface (with \(k = 0\)) of F. Then
\(F_x(x_0, y_0, z_0) = f_x(x_0, y_0)\) \(F_y(x_0, y_0, z_0) = f_y(x_0, y_0)\) \(F_z(x_0, y_0, z_0) = -1\)
so the equation becomes
\(f_x(x_0, y_0)(x - x_0) + f_y(x_0, y_0)(y - y_0) - (z - z_0) = 0\)
which is equivalent to our previous definition of a tangent plane. Thus our new, more general, definition of a tangent plane is consistent with the definition that was given for the special case.
EXAMPLE Find the equations of the tangent plane and normal line at the point \((-2, 1, -3)\) to the ellipsoid
\(\frac{x^2}{4} + y^2 + \frac{z^2}{9} = 3\)
Exercise 1
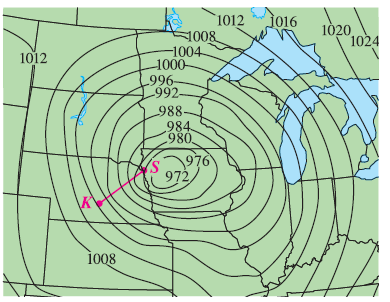
Level curves for barometric pressure (in millibars) are shown for 6:00 AM on a day in November. A deep low with pressure 972 mb is moving over northeast Iowa. The distance along the red line from K (Kearney, Nebraska) to S (Sioux City, Iowa) is 300 km. Estimate the value of the directional derivative of the pressure function at Kearney in the direction of Sioux City. What are the units of the directional derivative?
Exercise 2
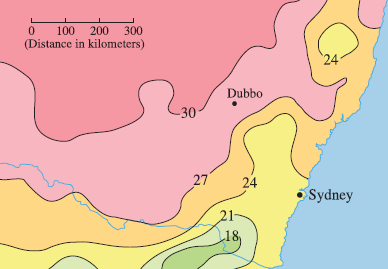
The contour map shows the average maximum temperature for November 2004 (in °C). Estimate the value of the directional derivative of this temperature function at Dubbo, New South Wales, in the direction of Sydney. What are the units?
Exercise 3
A table of values for the wind-chill index \(W = f(T, v)\) is given in Exercise 14.3.3 on page 923. Use the table to estimate the value of \(D_u f(-20, 30)\), where \(u = (i + j)/\sqrt{2}\).
Exercise 4
Find the directional derivative of \(f(x, y) = xy^3 - x^2\) at the point \((1, 2)\) in the direction indicated by the angle \(\theta = \pi/3\).
Exercise 5
Find the directional derivative of \(f(x, y) = y \cos(xy)\) at the point \((0, 1)\) in the direction indicated by the angle \(\theta = \pi/4\).
Exercise 6
Find the directional derivative of \(f(x, y) = \sqrt{2x + 3y}\) at the point \((3, 1)\) in the direction indicated by the angle \(\theta = -\pi/6\).
Exercise 7
For \(f(x, y) = x/y\) at point \(P(2, 1)\) with vector \(u = \langle 5/13, 12/13 \rangle\): (a) Find the gradient of f. (b) Evaluate the gradient at the point P. (c) Find the rate of change of f at P in the direction of the vector u.
Exercise 8
For \(f(x, y) = x^2 \ln y\) at point \(P(3, 1)\) with vector \(u = \langle 1/\sqrt{2}, -1/\sqrt{2} \rangle\): (a) Find the gradient of f. (b) Evaluate the gradient at the point P. (c) Find the rate of change of f at P in the direction of the vector u.
Exercise 9
For \(f(x, y, z) = x^2yz - xyz^3\) at point \(P(2, -1, 1)\) with vector \(u = \langle 0, 4/5, -3/5 \rangle\): (a) Find the gradient of f. (b) Evaluate the gradient at the point P. (c) Find the rate of change of f at P in the direction of the vector u.
Exercise 10
For \(f(x, y, z) = y^2e^{xyz}\) at point \(P(0, 1, -1)\) with vector \(u = \langle 3/13, 4/13, 12/13 \rangle\): (a) Find the gradient of f. (b) Evaluate the gradient at the point P. (c) Find the rate of change of f at P in the direction of the vector u.
Exercise 11
Find the directional derivative of the function \(f(x, y) = e^x \sin y\) at the point \((0, \pi/3)\) in the direction of the vector \(v = \langle -6, 8 \rangle\).
Exercise 12
Find the directional derivative of the function \(f(x, y) = \frac{x}{x^2 + y^2}\) at the point \((1, 2)\) in the direction of the vector \(v = \langle 3, 5 \rangle\).
Exercise 13
Find the directional derivative of the function \(g(s, t) = s\sqrt{t}\) at the point \((2, 4)\) in the direction of the vector \(v = 2i - j\).
Exercise 14
Find the directional derivative of the function \(g(u, v) = u^2e^{-v}\) at the point \((3, 0)\) in the direction of the vector \(v = 3i + 4j\).
Exercise 15
Find the directional derivative of the function \(f(x, y, z) = \sqrt{x^2y + y^2z}\) at the point \((1, 2, 3)\) in the direction of the vector \(v = \langle 2, -1, 2 \rangle\).
Exercise 16
Find the directional derivative of the function \(f(x, y, z) = xy^2 \tan^{-1}z\) at the point \((2, 1, 1)\) in the direction of the vector \(v = \langle 1, 1, 1 \rangle\).
Exercise 17
Find the directional derivative of the function \(h(r, s, t) = \ln(3r + 6s + 9t)\) at the point \((1, 1, 1)\) in the direction of the vector \(v = 4i + 12j + 6k\).
Exercise 18
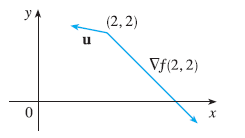
Use the figure to estimate \(D_u f(2, 2)\).
Exercise 19
Find the directional derivative of \(f(x, y) = \sqrt{xy}\) at \(P(2, 8)\) in the direction of \(Q(5, 4)\).
Exercise 20
Find the directional derivative of \(f(x, y, z) = xy^2z^3\) at \(P(2, 1, 1)\) in the direction of \(Q(0, -3, 5)\).
Exercise 21
Find the maximum rate of change of \(f(x, y) = 4y\sqrt{x}\) at the point \((4, 1)\) and the direction in which it occurs.
Exercise 22
Find the maximum rate of change of \(f(s, t) = te^s\) at the point \((0, 2)\) and the direction in which it occurs.
Exercise 23
Find the maximum rate of change of \(f(x, y) = \sin(xy)\) at the point \((1, 0)\) and the direction in which it occurs.
Exercise 24
Find the maximum rate of change of \(f(x, y, z) = x \ln(yz)\) at the point \((1, 2, 1/2)\) and the direction in which it occurs.
Exercise 25
Find the maximum rate of change of \(f(x, y, z) = x/(y + z)\) at the point \((8, 1, 3)\) and the direction in which it occurs.
Exercise 26
Find the maximum rate of change of \(f(p, q, r) = \arctan(pqr)\) at the point \((1, 2, 1)\) and the direction in which it occurs.
Exercise 27
- Show that a differentiable function \(f\) decreases most rapidly at x in the direction opposite to the gradient vector, that is, in the direction of \(-\nabla f(\mathbf{x})\).
- Use the result of part (a) to find the direction in which the function \(f(x, y) = x^4y - x^2y^3\) decreases fastest at the point \((2, -3)\).
Exercise 28
Find the directions in which the directional derivative of \(f(x, y) = x^2 + \sin(xy)\) at the point \((1, 0)\) has the value 1.
Exercise 29
Find all points at which the direction of fastest change of the function \(f(x, y) = x^2 + y^2 - 2x - 4y\) is \(\mathbf{i} + \mathbf{j}\).
Exercise 30
Near a buoy, the depth of a lake at the point with coordinates \((x, y)\) is \(z = 200 + 0.02x^2 - 0.001y^3\), where x, y, and z are measured in meters. A fisherman in a small boat starts at the point \((80, 60)\) and moves toward the buoy, which is located at \((0, 0)\). Is the water under the boat getting deeper or shallower when he departs? Explain.
Exercise 31
The temperature T in a metal ball is inversely proportional to the distance from the center of the ball, which we take to be the origin. The temperature at the point \((1, 2, 2)\) is 120°. (a) Find the rate of change of T at \((1, 2, 2)\) in the direction toward the point \((2, 1, 3)\). (b) Show that at any point in the ball the direction of greatest increase in temperature is given by a vector that points toward the origin.
Exercise 32
The temperature at a point \((x, y, z)\) is given by \(T(x, y, z) = 200e^{-x^2 - 3y^2 - 9z^2}\) where T is measured in °C and x, y, z in meters. (a) Find the rate of change of temperature at the point \(P(2, -1, 2)\) in the direction toward the point \((3, -3, 3)\). (b) In which direction does the temperature increase fastest at P? (c) Find the maximum rate of increase at P.
Exercise 33
Suppose that over a certain region of space the electrical potential V is given by \(V(x, y, z) = 5x^2 - 3xy + xyz\). (a) Find the rate of change of the potential at \(P(3, 4, 5)\) in the direction of the vector \(\mathbf{v} = \mathbf{i} + \mathbf{j} - \mathbf{k}\). (b) In which direction does V change most rapidly at P? (c) What is the maximum rate of change at P?
Exercise 34
Suppose you are climbing a hill whose shape is given by the equation \(z = 1000 - 0.005x^2 - 0.01y^2\), where x, y, and z are measured in meters, and you are standing at a point with coordinates \((60, 40, 966)\). The positive x-axis points east and the positive y-axis points north. (a) If you walk due south, will you start to ascend or descend? At what rate? (b) If you walk northwest, will you start to ascend or descend? At what rate? (c) In which direction is the slope largest? What is the rate of ascent in that direction? At what angle above the horizontal does the path in that direction begin?
Exercise 35
Let f be a function of two variables that has continuous partial derivatives and consider the points A(1, 3), B(3, 3), C(1, 7), and D(6, 15). The directional derivative of f at A in the direction of the vector \(\vec{AB}\) is 3 and the directional derivative at A in the direction of \(\vec{AC}\) is 26. Find the directional derivative of f at A in the direction of the vector \(\vec{AD}\).
Exercise 36
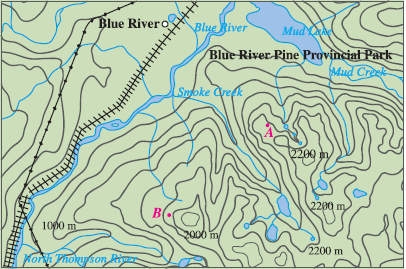
Shown is a topographic map of Blue River Pine Provincial Park in British Columbia. Draw curves of steepest descent from point A (descending to Mud Lake) and from point B.
Exercise 37
Show that the operation of taking the gradient of a function has the given property. Assume that u and v are differentiable functions of x and y and that a, b are constants. (a) \(\nabla(au + bv) = a\nabla u + b\nabla v\) (b) \(\nabla(uv) = u\nabla v + v\nabla u\) (c) \(\nabla(\frac{u}{v}) = \frac{v\nabla u - u\nabla v}{v^2}\) (d) \(\nabla u^n = nu^{n-1}\nabla u\)
Exercise 38
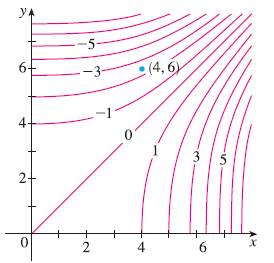
Sketch the gradient vector \(\nabla f(4, 6)\) for the function f whose level curves are shown. Explain how you chose the direction and length of this vector.
Exercise 39
The second directional derivative of \(f(x, y)\) is \(D^2_{\mathbf{u}}f(x, y) = D_{\mathbf{u}}[D_{\mathbf{u}}f(x, y)]\) If \(f(x, y) = x^3 + 5x^2y + y^3\) and \(\mathbf{u} = \langle \frac{3}{5}, \frac{4}{5} \rangle\), calculate \(D^2_{\mathbf{u}}f(2, 1)\).
Exercise 40
- If \(\mathbf{u} = \langle a, b \rangle\) is a unit vector and f has continuous second partial derivatives, show that \(D^2_{\mathbf{u}}f = f_{xx}a^2 + 2f_{xy}ab + f_{yy}b^2\)
- Find the second directional derivative of \(f(x, y) = xe^{2y}\) in the direction of \(\mathbf{v} = \langle 4, 6 \rangle\).
Exercise 41
Find equations of (a) the tangent plane and (b) the normal line to the given surface \(2(x - 2)^2 + (y - 1)^2 + (z - 3)^2 = 10\) at the specified point \((3, 3, 5)\).
Exercise 42
Find equations of (a) the tangent plane and (b) the normal line to the given surface \(x = y^2 + z^2 - 2\) at the specified point \((3, 1, -1)\).
Exercise 43
Find equations of (a) the tangent plane and (b) the normal line to the given surface \(xy^2z^3 = 8\) at the specified point \((2, 2, 1)\).
Exercise 44
Find equations of (a) the tangent plane and (b) the normal line to the given surface \(xy + yz + zx = 5\) at the specified point \((1, 2, 1)\).
Exercise 45
Find equations of (a) the tangent plane and (b) the normal line to the given surface \(x + y + z = e^{xyz}\) at the specified point \((0, 0, 1)\).
Exercise 46
Find equations of (a) the tangent plane and (b) the normal line to the given surface \(x^4 + y^4 + z^4 = 3x^2y^2z^2\) at the specified point \((1, 1, 1)\).
Exercise 47
Use a computer to graph the surface, the tangent plane, and the normal line on the same screen for \(xy + yz + zx = 3\) at \((1, 1, 1)\). Choose the domain carefully so that you avoid extraneous vertical planes. Choose the viewpoint so that you get a good view of all three objects.
Exercise 48
Use a computer to graph the surface, the tangent plane, and the normal line on the same screen for \(xyz = 6\) at \((1, 2, 3)\). Choose the domain carefully so that you avoid extraneous vertical planes. Choose the viewpoint so that you get a good view of all three objects.
Exercise 49
If \(f(x, y) = xy\), find the gradient vector \(\nabla f(3, 2)\) and use it to find the tangent line to the level curve \(f(x, y) = 6\) at the point \((3, 2)\). Sketch the level curve, the tangent line, and the gradient vector.
Exercise 50
If \(g(x, y) = x^2 + y^2 - 4x\), find the gradient vector \(\nabla g(1, 2)\) and use it to find the tangent line to the level curve \(g(x, y) = 1\) at the point \((1, 2)\). Sketch the level curve, the tangent line, and the gradient vector.
Exercise 51
Show that the equation of the tangent plane to the ellipsoid \(x^2/a^2 + y^2/b^2 + z^2/c^2 = 1\) at the point \((x_0, y_0, z_0)\) can be written as \(\frac{xx_0}{a^2} + \frac{yy_0}{b^2} + \frac{zz_0}{c^2} = 1\)
Exercise 52
Find the equation of the tangent plane to the hyperboloid \(x^2/a^2 + y^2/b^2 - z^2/c^2 = 1\) at \((x_0, y_0, z_0)\) and express it in a form similar to the one in Exercise 51.
Exercise 53
Show that the equation of the tangent plane to the elliptic paraboloid \(z/c = x^2/a^2 + y^2/b^2\) at the point \((x_0, y_0, z_0)\) can be written as \(\frac{2xx_0}{a^2} + \frac{2yy_0}{b^2} = \frac{z + z_0}{c}\)
Exercise 54
At what point on the ellipsoid \(x^2 + y^2 + 2z^2 = 1\) is the tangent plane parallel to the plane \(x + 2y + z = 1\)?
Exercise 55
Are there any points on the hyperboloid \(x^2 - y^2 - z^2 = 1\) where the tangent plane is parallel to the plane \(z = x + y\)?
Exercise 56
Show that the ellipsoid \(3x^2 + 2y^2 + z^2 = 9\) and the sphere \(x^2 + y^2 + z^2 - 8x - 6y - 8z + 24 = 0\) are tangent to each other at the point \((1, 1, 2)\). (This means that they have a common tangent plane at the point.)
Exercise 57
Show that every plane that is tangent to the cone \(x^2 + y^2 = z^2\) passes through the origin.
Exercise 58
Show that every normal line to the sphere \(x^2 + y^2 + z^2 = r^2\) passes through the center of the sphere.
Exercise 59
Where does the normal line to the paraboloid \(z = x^2 + y^2\) at the point \((1, 1, 2)\) intersect the paraboloid a second time?
Exercise 60
At what points does the normal line through the point \((1, 2, 1)\) on the ellipsoid \(4x^2 + y^2 + 4z^2 = 12\) intersect the sphere \(x^2 + y^2 + z^2 = 102\)?
Exercise 61
Show that the sum of the x-, y-, and z-intercepts of any tangent plane to the surface \(\sqrt{x} + \sqrt{y} + \sqrt{z} = \sqrt{c}\) is a constant.
Exercise 62
Show that the pyramids cut off from the first octant by any tangent planes to the surface \(xyz = 1\) at points in the first octant must all have the same volume.
Exercise 63
Find parametric equations for the tangent line to the curve of intersection of the paraboloid \(z = x^2 + y^2\) and the ellipsoid \(4x^2 + y^2 + z^2 = 9\) at the point \((-1, 1, 2)\).
Exercise 64
- The plane \(y + z = 3\) intersects the cylinder \(x^2 + y^2 = 5\) in an ellipse. Find parametric equations for the tangent line to this ellipse at the point \((1, 2, 1)\).
- Graph the cylinder, the plane, and the tangent line on the same screen.
Exercise 65
Where does the helix \(\mathbf{r}(t) = \langle \cos(\pi t), \sin(\pi t), t \rangle\) intersect the paraboloid \(z = x^2 + y^2\)? What is the angle of intersection between the helix and the paraboloid? (This is the angle between the tangent vector to the curve and the tangent plane to the paraboloid.)
Exercise 66
The helix \(\mathbf{r}(t) = \langle \cos(\pi t/2), \sin(\pi t/2), t \rangle\) intersects the sphere \(x^2 + y^2 + z^2 = 2\) in two points. Find the angle of intersection at each point.
Exercise 67
Two surfaces are called orthogonal at a point of intersection if their normal lines are perpendicular at that point. Show that surfaces with equations \(F(x, y, z) = 0\) and \(G(x, y, z) = 0\) are orthogonal at a point P where \(\nabla F \neq \mathbf{0}\) and \(\nabla G \neq \mathbf{0}\) if and only if \(F_x G_x + F_y G_y + F_z G_z = 0\) at P
Use part (a) to show that the surfaces \(z^2 = x^2 + y^2\) and \(x^2 + y^2 + z^2 = r^2\) are orthogonal at every point of intersection. Can you see why this is true without using calculus?
Exercise 68
- Show that the function \(f(x, y) = \sqrt[3]{xy}\) is continuous and the partial derivatives \(f_x\) and \(f_y\) exist at the origin but the directional derivatives in all other directions do not exist.
- Graph f near the origin and comment on how the graph confirms part (a).
Exercise 69
Suppose that the directional derivatives of \(f(x, y)\) are known at a given point in two nonparallel directions given by unit vectors u and v. Is it possible to find \(\nabla f\) at this point? If so, how would you do it?
Exercise 70
Show that if \(z = f(x, y)\) is differentiable at \(\mathbf{x}_0 = (x_0, y_0)\), then \(\lim_{\mathbf{x} \to \mathbf{x}_0} \frac{f(\mathbf{x}) - f(\mathbf{x}_0) - \nabla f(\mathbf{x}_0) \cdot (\mathbf{x} - \mathbf{x}_0)}{|\mathbf{x} - \mathbf{x}_0|} = 0\)
[Hint: Use Definition Directly]