Section 14.7: Max Min Problems
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 14.7: Max Min Problems |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 2:12 AM |
Table of contents
- Learning Outcomes: Maximum and Minimum Values
- Introduction
- How to find max/min?
- Critical Points
- Second derivative Test
- Sample Application Problem
- Sample Application Problem
- Absolute Maximum and Minimum Values
- Example absolute min-max problem
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
- Exercise 49
- Exercise 50
- Exercise 51
- Exercise 52
- Exercise 53
- Exercise 54
- Exercise 55
- Exercise 56
- Exercise 57
- Exercise 58
- Exercise 59
- Exercise 60
Learning Outcomes: Maximum and Minimum Values
- In this section we will learn to use partial derivatives to solve max-min problems
Introduction
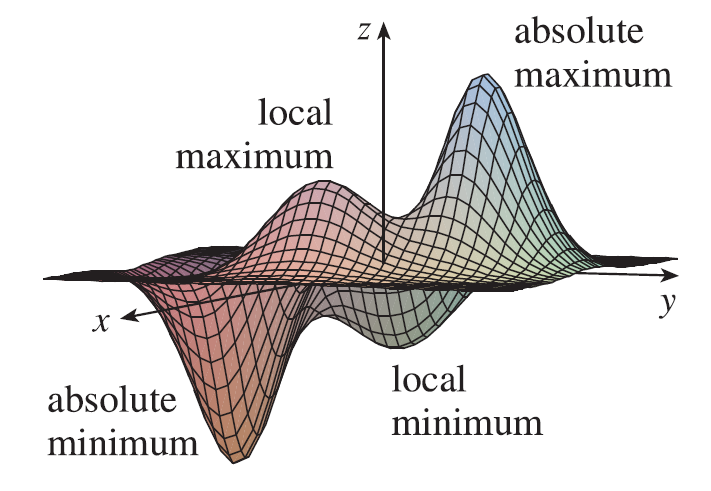
Look at the hills and valleys in the graph of \(f\) shown in Figure There are two points \((a, b)\) where \(f\) has a local maximum, that is, where \(f(a, b)\) is larger than nearby values of \(f(x, y)\). The larger of these two values is the absolute maximum. Likewise, \(f\) has two local minima, where \(f(a, b)\) is smaller than nearby values. The smaller of these two values is the absolute minimum.
Definition: Local maximum & minimum: A function of two variables has a local maximum at \((a, b)\) if \(f(x, y) \le f(a, b)\) when \((x, y)\) is near \((a, b)\). [This means that \(f(x, y) \le f(a, b)\) for all points \((x, y)\) in some disk with center \((a, b)\).] The number \(f(a, b)\) is called a local maximum value. If \(f(x, y) \ge f(a, b)\) when \((x, y)\) is near \((a, b)\), then \(f\) has a local minimum at \((a, b)\) and \(f(a, b)\) is a local minimum value.
If the inequalities in Definition hold for all points \((x, y)\) in the domain of \(f\), then \(f\) has an absolute maximum (or absolute minimum) at \((a, b)\).
How to find max/min?
Theorem If \(f\) has a local maximum or minimum at \((a, b)\) and the first-order partial derivatives of \(f\) exist there, then \(f_x(a, b) = 0\) and \(f_y(a, b) = 0\).
PROOF Let \(g(x) = f(x, b)\). If \(f\) has a local maximum (or minimum) at \((a, b)\), then \(g\) has a local maximum (or minimum) at \(a\), so \(g'(a) = 0\) by Fermat’s Theorem. But \(g'(a) = f_x(a, b)\) and so \(f_x(a, b) = 0\). Similarly, by applying Fermat’s Theorem to the function \(G(y) = f(a, y)\), we obtain \(f_y(a, b) = 0\).
Notice that the conclusion of Theorem 2 can be stated in the notation of gradient vectors as \(\nabla f(a, b) = \mathbf{0}\).
If we put \(f_x(a, b) = 0\) and \(f_y(a, b) = 0\) in the equation of a tangent plane, we get \(z = z_0\). Thus the geometric interpretation of Theorem 2 is that if the graph of \(f\) has a tangent plane at a local maximum or minimum, then the tangent plane must be horizontal.
Critical Points
A point \((a, b)\) is called a critical point (or stationary point) of \(f\) if \(f_x(a, b) = 0\) and \(f_y(a, b) = 0\), or if one of these partial derivatives does not exist.
Theorem says that if \(f\) has a local maximum or minimum at \((a, b)\), then \((a, b)\) is a critical point of \(f\). However, as in single-variable calculus, not all critical points give rise to maxima or minima. At a critical point, a function could have a local maximum or a local minimum or neither.
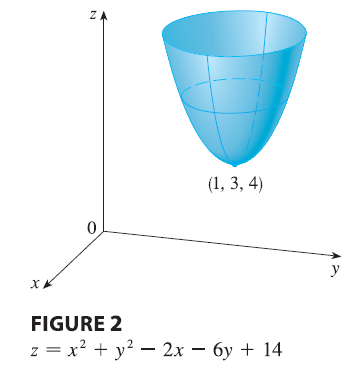
EXAMPLE Let \(f(x, y) = x^2 + y^2 - 2x - 6y + 14\). Then \[ f_x(x, y) = 2x - 2 \quad f_y(x, y) = 2y - 6 \] These partial derivatives are equal to 0 when \(x = 1\) and \(y = 3\), so the only critical point is \((1, 3)\). By completing the square, we find that \[ f(x, y) = 4 + (x - 1)^2 + (y - 3)^2 \] Since \((x - 1)^2 \ge 0\) and \((y - 3)^2 \ge 0\), we have \(f(x, y) \ge 4\) for all values of \(x\) and \(y\). Therefore \(f(1, 3) = 4\) is a local minimum, and in fact it is the absolute minimum of \(f\). This can be confirmed geometrically from the graph of \(f\), which is the elliptic paraboloid with vertex \((1, 3, 4)\) shown in Figure 2.
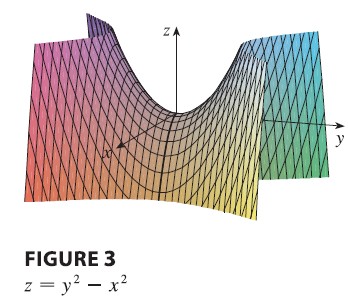
EXAMPLE 2 Find the extreme values of \(f(x, y) = y^2 - x^2\).
Example illustrates the fact that a function need not have a maximum or minimum value at a critical point. Figure 3 shows how this is possible. The graph of \(f\) is the hyperbolic paraboloid \(z = y^2 - x^2\), which has a horizontal tangent plane (\(z = 0\)) at the origin. You can see that \(f(0, 0) = 0\) is a maximum in the direction of the x-axis but a minimum in the direction of the y-axis. Near the origin the graph has the shape of a saddle and so \((0, 0)\) is called a saddle point of \(f\).
Second derivative Test
We need to be able to determine whether or not a function has an extreme value at a critical point. The following test, which is proved at the end of this section, is analogous to the Second Derivative Test for functions of one variable.
Second Derivatives Test Suppose the second partial derivatives of \(f\) are continuous on a disk with center \((a, b)\), and suppose that \(f_x(a, b) = 0\) and \(f_y(a, b) = 0\) [that is, \((a, b)\) is a critical point of \(f\)]. Let \[ D = D(a, b) = f_{xx}(a, b)f_{yy}(a, b) - [f_{xy}(a, b)]^2 \] (a) If \(D > 0\) and \(f_{xx}(a, b) > 0\), then \(f(a, b)\) is a local minimum. (b) If \(D > 0\) and \(f_{xx}(a, b) < 0\), then \(f(a, b)\) is a local maximum. (c) If \(D < 0\), then \(f(a, b)\) is not a local maximum or minimum.
NOTE 1 In case (c) the point \((a, b)\) is called a saddle point of \(f\) and the graph of \(f\) crosses its tangent plane at \((a, b)\). NOTE 2 If \(D = 0\), the test gives no information: \(f\) could have a local maximum or local minimum at \((a, b)\), or \((a, b)\) could be a saddle point of \(f\). NOTE 3 To remember the formula for \(D\), it’s helpful to write it as a determinant: \[ D = \begin{vmatrix} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \end{vmatrix} = f_{xx}f_{yy} - (f_{xy})^2 \]
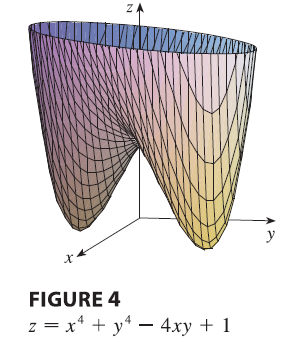
EXAMPLE Find the local maximum and minimum values and saddle points of \(f(x, y) = x^4 + y^4 - 4xy + 1\).
EXAMPLE Find and classify the critical points of the function \[ f(x, y) = 10x^2y - 5x^2 - 4y^2 - x^4 - 2y^4 \] Also find the highest point on the graph of \(f\).
Sample Application Problem
EXAMPLE Find the shortest distance from the point \((1, 0, -2)\) to the plane \(x + 2y + z = 4\).
Sample Application Problem
EXAMPLE A rectangular box without a lid is to be made from 12 m\(^2\) of cardboard. Find the maximum volume of such a box.
Absolute Maximum and Minimum Values
For a function \(f\) of one variable, the Extreme Value Theorem says that if \(f\) is continuous on a closed interval \([a, b]\), then \(f\) has an absolute minimum value and an absolute maximum value. According to the Closed Interval Method, we found these by evaluating \(f\) not only at the critical numbers but also at the endpoints \(a\) and \(b\).
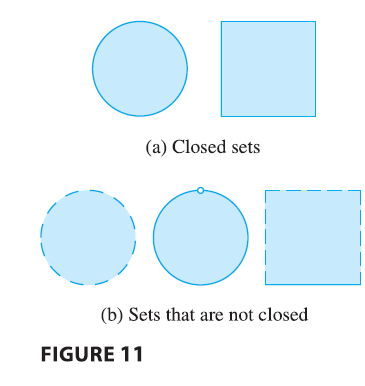
There is a similar situation for functions of two variables. Just as a closed interval contains its endpoints, a closed set in \(\mathbb{R}^2\) is one that contains all its boundary points. [A boundary point of \(D\) is a point \((a, b)\) such that every disk with center \((a, b)\) contains points in \(D\) and also points not in \(D\).] For instance, the disk
\[ D = \{(x, y) | x^2 + y^2 \le 1\} \]
which consists of all points on or inside the circle \(x^2 + y^2 = 1\), is a closed set because it contains all of its boundary points (which are the points on the circle \(x^2 + y^2 = 1\)). But if even one point on the boundary curve were omitted, the set would not be closed.
A bounded set in \(\mathbb{R}^2\) is one that is contained within some disk. In other words, it is finite in extent. Then, in terms of closed and bounded sets, we can state the following counterpart of the Extreme Value Theorem in two dimensions.
Extreme Value Theorem for Functions of Two Variables If \(f\) is continuous on a closed, bounded set \(D\) in \(\mathbb{R}^2\), then \(f\) attains an absolute maximum value \(f(x_1, y_1)\) and an absolute minimum value \(f(x_2, y_2)\) at some points \((x_1, y_1)\) and \((x_2, y_2)\) in \(D\).
To find the extreme values guaranteed by Theorem, we note that, by a previous Theorem , if \(f\) has an extreme value at \((x_1, y_1)\), then \((x_1, y_1)\) is either a critical point of \(f\) or a boundary point of \(D\). Thus we have the following extension of the Closed Interval Method.
Steps to find Absolute Min-max
To find the absolute maximum and minimum values of a continuous function \(f\) on a closed, bounded set \(D\): 1. Find the values of \(f\) at the critical points of \(f\) in \(D\). 2. Find the extreme values of \(f\) on the boundary of \(D\). 3. The largest of the values from steps 1 and 2 is the absolute maximum value; the smallest of these values is the absolute minimum value.
Example absolute min-max problem
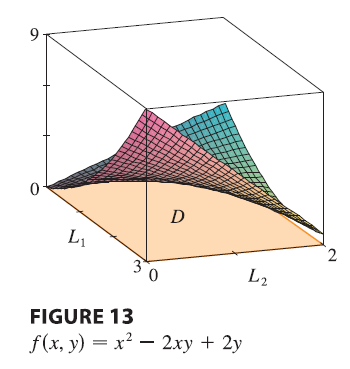
EXAMPLE Find the absolute maximum and minimum values of the function \(f(x, y) = x^2 - 2xy + 2y\) on the rectangle \(D = \{(x, y) | 0 \le x \le 3, 0 \le y \le 2\}\).
Exercise 1
Suppose (1, 1) is a critical point of a function f with continuous second derivatives. In each case, what can you say about f? (a) \(f_{xx}(1, 1) = 4\), \(f_{xy}(1, 1) = 1\), \(f_{yy}(1, 1) = 2\) (b) \(f_{xx}(1, 1) = 4\), \(f_{xy}(1, 1) = 3\), \(f_{yy}(1, 1) = 2\)
Exercise 2
Suppose (0, 2) is a critical point of a function g with continuous second derivatives. In each case, what can you say about g? (a) \(g_{xx}(0, 2) = -1\), \(g_{xy}(0, 2) = 6\), \(g_{yy}(0, 2) = 1\) (b) \(g_{xx}(0, 2) = -1\), \(g_{xy}(0, 2) = 2\), \(g_{yy}(0, 2) = -8\) (c) \(g_{xx}(0, 2) = 4\), \(g_{xy}(0, 2) = 6\), \(g_{yy}(0, 2) = 9\)
Exercise 3
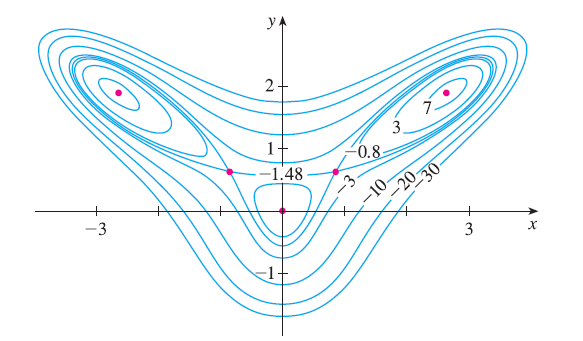
Use the level curves in the figure to predict the location of the critical points of \(f(x, y) = 4 + x^3 + y^3 - 3xy\) and whether f has a saddle point or a local maximum or minimum at each critical point. Explain your reasoning. Then use the Second Derivatives Test to confirm your predictions.
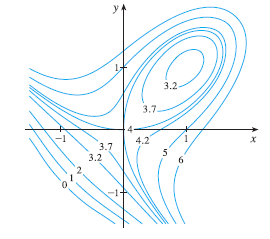
Exercise 4
Use the level curves in the figure to predict the location of the critical points of \(f(x, y) = 3x - x^3 - 2y^2 + y^4\) and whether f has a saddle point or a local maximum or minimum at each critical point. Explain your reasoning. Then use the Second Derivatives Test to confirm your predictions.
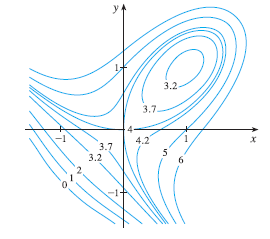
Exercise 5
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = x^2 + xy + y^2 + y\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 6
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = xy - 2x - 2y - x^2 - y^2\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 7
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = (x - y)(1 - xy)\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 8
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = y(e^x - 1)\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 9
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = x^3y + 12x^2 - 8y\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 10
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = 2x^3 + xy^2 + 5x^2 + y^2\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 11
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = x^3 - 3x + 3xy^2\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 12
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = x^4 + y^4 - 4x^2 - 2y^2\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 13
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = x^4 - 2x^2 + y^3 - 3y\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 14
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = y \cos x\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 15
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = e^x \cos y\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 16
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = xye^{-(x^2+y^2)/2}\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 17
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = xy + e^{-xy}\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 18
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = (x^2 + y^2)e^{y^2-x^2}\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 19
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = y^2 - 2y \cos x\), \(-1 \le x \le 7\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 20
Find the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = \sin x \sin y\), \(-\pi < x < \pi\), \(-\pi < y < \pi\). If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function.
Exercise 21
Show that \(f(x, y) = x^2 + 4y^2 - 4xy + 2\) has an infinite number of critical points and that \(D = 0\) at each one. Then show that \(f\) has a local (and absolute) minimum at each critical point.
Exercise 22
Show that \(f(x, y) = x^2ye^{-x^2-y^2}\) has maximum values at \((\pm 1, 1/\sqrt{2})\) and minimum values at \((\pm 1, -1/\sqrt{2})\). Show also that \(f\) has infinitely many other critical points and \(D = 0\) at each of them. Which of them give rise to maximum values? Minimum values? Saddle points?
Exercise 23
Use a graph or level curves or both to estimate the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = x^2 + y^2 + x^{-2}y^{-2}\). Then use calculus to find these values precisely.
Exercise 24
Use a graph or level curves or both to estimate the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = (x - y)e^{-x^2-y^2}\). Then use calculus to find these values precisely.
Exercise 25
Use a graph or level curves or both to estimate the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = \sin x + \sin y + \sin(x + y)\), \(0 \le x \le 2\pi\), \(0 \le y \le 2\pi\). Then use calculus to find these values precisely.
Exercise 26
Use a graph or level curves or both to estimate the local maximum and minimum values and saddle point(s) of the function \(f(x, y) = \sin x + \sin y + \cos(x + y)\), \(0 \le x \le \pi/4\), \(0 \le y \le \pi/4\). Then use calculus to find these values precisely.
Exercise 27
Use a graphing device as in Example 4 (or Newton’s method or solve numerically using a calculator or computer) to find the critical points of \(f(x, y) = x^4 + y^4 - 4x^2y + 2y\) correct to three decimal places. Then classify the critical points and find the highest or lowest points on the graph, if any.
Exercise 28
Use a graphing device as in Example 4 (or Newton’s method or solve numerically using a calculator or computer) to find the critical points of \(f(x, y) = y^6 - 2y^4 + x^2 - y^2 + y\) correct to three decimal places. Then classify the critical points and find the highest or lowest points on the graph, if any.
Exercise 29
Use a graphing device as in Example 4 (or Newton’s method or solve numerically using a calculator or computer) to find the critical points of \(f(x, y) = x^4 + y^3 - 3x^2 + y^2 + x - 2y + 1\) correct to three decimal places. Then classify the critical points and find the highest or lowest points on the graph, if any.
Exercise 30
Use a graphing device as in Example 4 (or Newton’s method or solve numerically using a calculator or computer) to find the critical points of \(f(x, y) = 20e^{-x^2-y^2} \sin 3x \cos 3y\), \(|x| \le 1\), \(|y| \le 1\) correct to three decimal places. Then classify the critical points and find the highest or lowest points on the graph, if any.
Exercise 31
Find the absolute maximum and minimum values of \(f(x, y) = x^2 + y^2 - 2x\) on the set D, where D is the closed triangular region with vertices (2, 0), (0, 2), and (0, -2).
Exercise 32
Find the absolute maximum and minimum values of \(f(x, y) = x + y - xy\) on the set D, where D is the closed triangular region with vertices (0, 0), (0, 2), and (4, 0).
Exercise 33
Find the absolute maximum and minimum values of \(f(x, y) = x^2 + y^2 + x^2y + 4\) on the set \(D = \{(x, y) | |x| \le 1, |y| \le 1\}\).
Exercise 34
(Different from book)
Find the absolute maximum and minimum values of \(f(x, y) = 4x + 6y - x^2 - y^2\) on the set \(D = \{(x, y) | 0 \le x \le 4, 0 \le y \le 5\}\).
Exercise 35
Find the absolute maximum and minimum values of \(f(x, y) = x^2 + 2y^2 - 2x - 4y + 1\) on the set \(D = \{(x, y) | 0 \le x \le 2, 0 \le y \le 3\}\).
Exercise 36
Find the absolute maximum and minimum values of \(f(x, y) = xy^2\) on the set \(D = \{(x, y) | x \ge 0, y \ge 0, x^2 + y^2 \le 3\}\).
Exercise 37
Find the absolute maximum and minimum values of \(f(x, y) = 2x^3 + y^4\) on the set \(D = \{(x, y) | x^2 + y^2 \le 1\}\).
Exercise 38
Find the absolute maximum and minimum values of \(f(x, y) = x^3 - 3x - y^3 + 12y\) on the set D, where D is the quadrilateral whose vertices are (-2, 3), (2, 3), (2, 2), and (-2, -2).
Exercise 39
For functions of one variable it is impossible for a continuous function to have two local maxima and no local minimum. But for functions of two variables such functions exist. Show that the function \(f(x, y) = -(x^2 - 1)^2 - (x^2y - x - 1)^2\) has only two critical points, but has local maxima at both of them. Then use a computer to produce a graph with a carefully chosen domain and viewpoint to see how this is possible.
Exercise 40
If a function of one variable is continuous on an interval and has only one critical number, then a local maximum has to be an absolute maximum. But this is not true for functions of two variables. Show that the function \(f(x, y) = 3xe^y - x^3 - e^{3y}\) has exactly one critical point, and that f has a local maximum there that is not an absolute maximum. Then use a computer to produce a graph with a carefully chosen domain and viewpoint to see how this is possible.
Exercise 41
Find the shortest distance from the point (2, 0, -3) to the plane \(x + y + z = 1\).
Exercise 42
Find the point on the plane \(x - 2y + 3z = 6\) that is closest to the point (0, 1, 1).
Exercise 43
Find the points on the cone \(z^2 = x^2 + y^2\) that are closest to the point (4, 2, 0).
Exercise 44
Find the points on the surface \(y^2 = 9 + xz\) that are closest to the origin.
Exercise 45
Find three positive numbers whose sum is 100 and whose product is a maximum.
Exercise 46
Find three positive numbers whose sum is 12 and the sum of whose squares is as small as possible.
Exercise 47
Find the maximum volume of a rectangular box that is inscribed in a sphere of radius r.
Exercise 48
Find the dimensions of the box with volume 1000 cm\(^3\) that has minimal surface area.
Exercise 49
Find the volume of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the plane \(x + 2y + 3z = 6\).
Exercise 50
Find the dimensions of the rectangular box with largest volume if the total surface area is given as 64 cm\(^2\).
Exercise 51
Find the dimensions of a rectangular box of maximum volume such that the sum of the lengths of its 12 edges is a constant c.
Exercise 52
The base of an aquarium with given volume V is made of slate and the sides are made of glass. If slate costs five times as much (per unit area) as glass, find the dimensions of the aquarium that minimize the cost of the materials.
Exercise 53
A cardboard box without a lid is to have a volume of 32,000 cm\(^3\). Find the dimensions that minimize the amount of cardboard used.
Exercise 54
A rectangular building is being designed to minimize heat loss. The east and west walls lose heat at a rate of 10 units/m\(^2\) per day, the north and south walls at a rate of 8 units/m\(^2\) per day, the floor at a rate of 1 unit/m\(^2\) per day, and the roof at a rate of 5 units/m\(^2\) per day. Each wall must be at least 30 m long, the height must be at least 4 m, and the volume must be exactly 4000 m\(^3\). (a) Find and sketch the domain of the heat loss as a function of the lengths of the sides. (b) Find the dimensions that minimize heat loss. (Check both the critical points and the points on the boundary of the domain.) (c) Could you design a building with even less heat loss if the restrictions on the lengths of the walls were removed?
Exercise 55
If the length of the diagonal of a rectangular box must be L, what is the largest possible volume?
Exercise 56
A model for the yield Y of an agricultural crop as a function of the nitrogen level N and phosphorus level P in the soil (measured in appropriate units) is \(Y(N, P) = k N P e^{-N-P}\) where k is a positive constant. What levels of nitrogen and phosphorus result in the best yield?
Exercise 57
The Shannon index is a measure of diversity in an ecosystem. For the case of three species, it is defined as \(H = -p_1 \ln p_1 - p_2 \ln p_2 - p_3 \ln p_3\) where \(p_i\) is the proportion of species i in the ecosystem. (a) Express H as a function of two variables \(p_1\) and \(p_2\) using the fact that \(p_1 + p_2 + p_3 = 1\). (b) What is the domain of H? (c) Find the maximum value of H. For what values of \(p_1, p_2, p_3\) does it occur?
Exercise 58
Three alleles (alternative versions of a gene) A, B, and O determine the four blood types A (AA or AO), B (BB or BO), O (OO), and AB. The Hardy-Weinberg Law states that the proportion of individuals in a population who carry two different alleles is \(P = 2pq + 2pr + 2rq\) where p, q, and r are the proportions of A, B, and O in the population. Use the fact that \(p + q + r = 1\) to show that P is at most 2/3.
Exercise 59
Suppose that a scientist has reason to believe that two quantities x and y are related linearly, that is, \(y = mx + b\), at least approximately, for some values of m and b. The scientist performs an experiment and collects data in the form of points \((x_1, y_1), (x_2, y_2), ..., (x_n, y_n)\), and then plots these points. The points don’t lie exactly on a straight line, so the scientist wants to find constants m and b so that the line \(y = mx + b\) “fits” the points as well as possible.
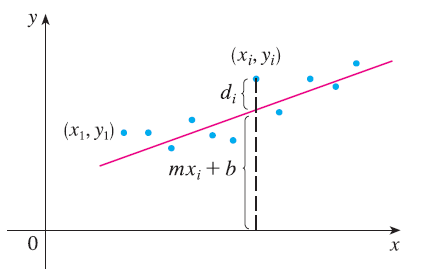
Let \(d_i = y_i - (mx_i + b)\) be the vertical deviation of the point \((x_i, y_i)\) from the line. The method of least squares determines m and b so as to minimize \(\sum_{i=1}^n d_i^2\), the sum of the squares of these deviations. Show that, according to this method, the line of best fit is obtained when \(m \sum_{i=1}^n x_i + bn = \sum_{i=1}^n y_i\) and \(m \sum_{i=1}^n x_i^2 + b \sum_{i=1}^n x_i = \sum_{i=1}^n x_i y_i\) Thus the line is found by solving these two equations in the two unknowns m and b.
Exercise 60
Find an equation of the plane that passes through the point (1, 2, 3) and cuts off the smallest volume in the first octant.