Section 15.2: Integration over general 2d regions
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 15.2: Integration over general 2d regions |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 3:57 AM |
Table of contents
- Learning outcomes:
- Definition of integral over general region
- Type 1 - region
- Type II region
- Example - Type I
- Example
- Example
- Example:
- Example - Change order of integration
- Properties of Double Integrals
- Using double integration to find area
- Lower and upper bounds on integration
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
- Exercise 49
- Exercise 50
- Exercise 51
- Exercise 52
- Exercise 53
- Exercise 54
- Exercise 55
- Exercise 56
- Exercise 57
- Exercise 58
- Exercise 59
- Exercise 60
- Exercise 61
- Exercise 62
- Exercise 63
- Exercise 64
- Exercise 65
- Exercise 66
- Exercise 67
- Exercise 68
- Exercise 69
- Exercise 70
Learning outcomes:
- Double Integration over general (non-rectangular) regions
Definition of integral over general region
For single integrals, the region over which we integrate is always an interval. But for double integrals, we want to be able to integrate a function \(f\) not just over rectangles but also over regions \(D\) of more general shape, such as the one illustrated in Figure 1.
We suppose that \(D\) is a bounded region, which means that \(D\) can be enclosed in a rectangular region \(R\) as in Figure 2. Then we define a new function \(F\) with domain \(R\) by \[ F(x, y) = \begin{cases} f(x, y) & \text{if } (x, y) \text{ is in } D \\ 0 & \text{if } (x, y) \text{ is in } R \text{ but not in } D \end{cases} \tag{1} \]
If \(F\) is integrable over \(R\), then we define the double integral of f over D by \[ \iint_D f(x, y) dA = \iint_R F(x, y) dA \tag{2} \] where F is given by Equation 1.
In the case where \(f(x, y) \ge 0\), we can still interpret \(\iint_D f(x, y) dA\) as the volume of the solid that lies above \(D\) and under the surface \(z = f(x, y)\) (the graph of \(f\)). You can see that this is reasonable by comparing the graphs of \(f\) and \(F\) in Figures 3 and 4 and remembering that \(\iint_R F(x, y) dA\) is the volume under the graph of \(F\).
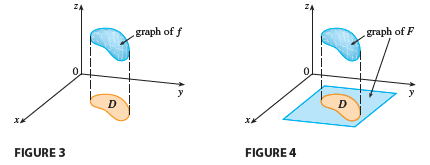
Figure 4 also shows that \(F\) is likely to have discontinuities at the boundary points of \(D\). Nonetheless, if \(f\) is continuous on \(D\) and the boundary curve of \(D\) is “well behaved” (in a sense outside the scope of this book), then it can be shown that \(\iint_R F(x, y) dA\) exists and therefore \(\iint_D f(x, y) dA\) exists. In particular, this is the case for the following two types of regions.
Type 1 - region
A plane region \(D\) is said to be of type I if it lies between the graphs of two continuous functions of \(x\), that is, \[ D = \{(x, y) | a \le x \le b, g_1(x) \le y \le g_2(x)\} \] where \(g_1\) and \(g_2\) are continuous on \([a, b]\). Some examples of type I regions are shown in Figure below.
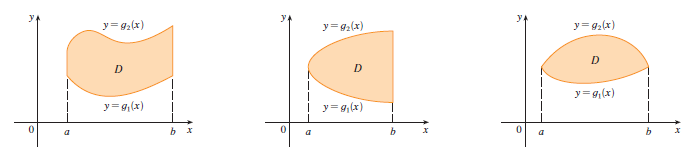
In order to evaluate \(\iint_D f(x, y) dA\) when \(D\) is a region of type I, we choose a rectangle \(R = [a, b] \times [c, d]\) that contains \(D\), as in Figure 6, and we let \(F\) be the function given by Equation 1; that is, \(F\) agrees with \(f\) on \(D\) and \(F\) is 0 outside \(D\). Then, by Fubini’s Theorem, \[ \iint_D f(x, y) dA = \iint_R F(x, y) dA = \int_a^b \int_c^d F(x, y) dy dx \] Observe that \(F(x, y) = 0\) if \(y < g_1(x)\) or \(y > g_2(x)\) because \((x, y)\) then lies outside \(D\). Therefore \[ \int_c^d F(x, y) dy = \int_{g_1(x)}^{g_2(x)} F(x, y) dy = \int_{g_1(x)}^{g_2(x)} f(x, y) dy \] because \(F(x, y) = f(x, y)\) when \(g_1(x) \le y \le g_2(x)\). Thus we have the following formula that enables us to evaluate the double integral as an iterated integral.
If f is continuous on a type I region \(D\) such that
\[ D = \{(x, y) | a \le x \le b, g_1(x) \le y \le g_2(x)\}, \] then \[ \iint_D f(x, y) dA = \int_a^b \int_{g_1(x)}^{g_2(x)} f(x, y) dy dx \tag{3} \] The integral on the right side of (3) is an iterated integral that is similar to the ones we considered in the preceding section, except that in the inner integral we regard \(x\) as being constant not only in \(f(x, y)\) but also in the limits of integration, \(g_1(x)\) and \(g_2(x)\).
Type II region
We also consider plane regions of type II, which can be expressed as \[ D = \{(x, y) | c \le y \le d, h_1(y) \le x \le h_2(y)\} \tag{4} \] where \(h_1\) and \(h_2\) are continuous. Two such regions are illustrated in Figure 7.
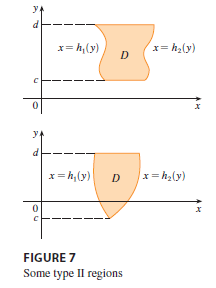
Using the same methods that were used in establishing (3), we can show that \[ \iint_D f(x, y) dA = \int_c^d \int_{h_1(y)}^{h_2(y)} f(x, y) dx dy \tag{5} \] where \(D\) is a type II region given by Equation 4.
Example - Type I
EXAMPLE 1 Evaluate \(\iint_D (x + 2y) dA\), where \(D\) is the region bounded by the parabolas \(y = 2x^2\) and \(y = 1 + x^2\).
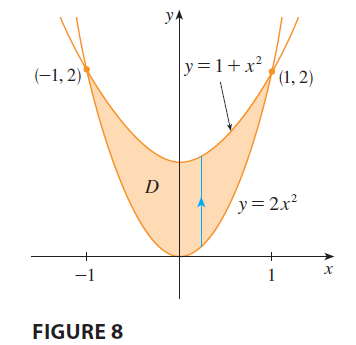
Example
EXAMPLE 2 Find the volume of the solid that lies under the paraboloid \(z = x^2 + y^2\) and above the region \(D\) in the \(xy\)-plane bounded by the line \(y = 2x\) and the parabola \(y = x^2\).
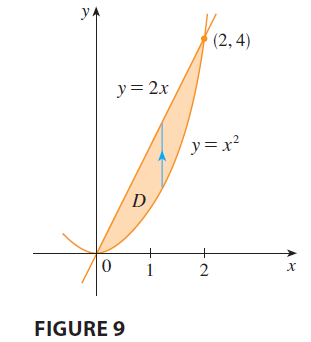
Type 1 Solution
Type II Solution
Example
EXAMPLE 3 Evaluate \(\iint_D xy dA\), where \(D\) is the region bounded by the line \(y = x - 1\) and the parabola \(y^2 = 2x + 6\).
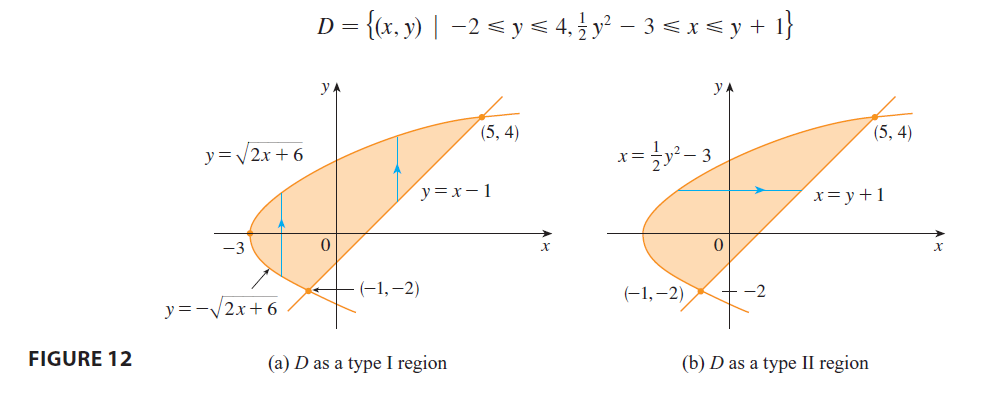
Example:
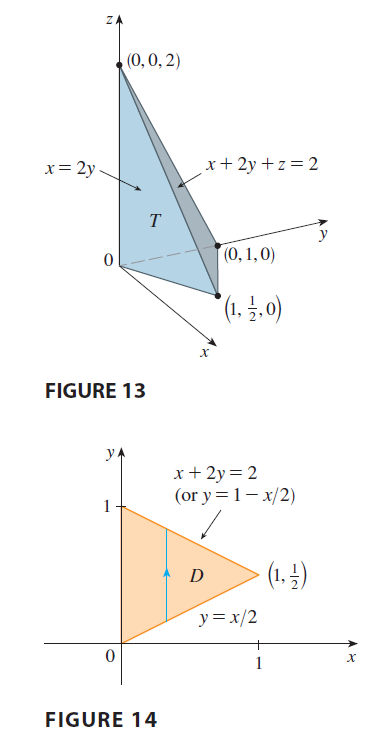
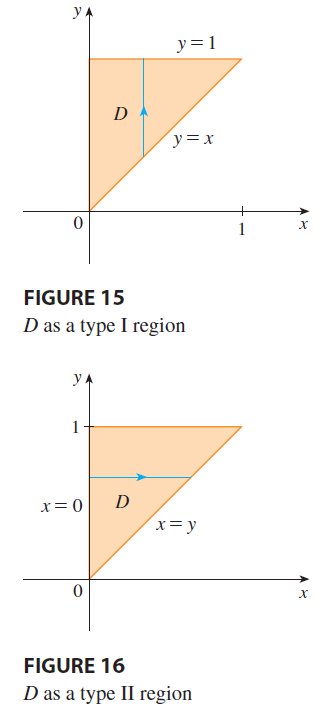
EXAMPLE 4 Find the volume of the tetrahedron bounded by the planes \(x + 2y + z = 2, x = 2y, x = 0,\) and \(z = 0\).
Example - Change order of integration
EXAMPLE 5 Evaluate the iterated integral \(\int_0^1 \int_x^1 \sin(y^2) dy dx\).
Properties of Double Integrals
General regions the properties follow from Definition.
\[ \iint_D [f(x, y) + g(x, y)] dA = \iint_D f(x, y) dA + \iint_D g(x, y) dA \tag{6} \]
\[ \iint_D cf(x, y) dA = c \iint_D f(x, y) dA \quad \text{where c is a constant} \tag{7} \]
If \(f(x, y) \ge g(x, y)\) for all \((x, y)\) in \(D\), then
\[ \iint_D f(x, y) dA \ge \iint_D g(x, y) dA \tag{8} \]
The next property of double integrals is similar to the property of single integrals given by the equation \(\int_a^c f(x) dx = \int_a^b f(x) dx + \int_b^c f(x) dx\). If \(D = D_1 \cup D_2\), where \(D_1\) and \(D_2\) don’t overlap except perhaps on their boundaries (see Figure 17), then
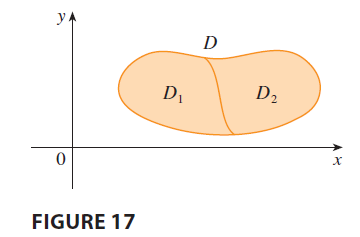
\[ \iint_D f(x, y) dA = \iint_{D_1} f(x, y) dA + \iint_{D_2} f(x, y) dA \tag{9} \] Property 9 can be used to evaluate double integrals over regions \(D\) that are neither type I nor type II but can be expressed as a union of regions of type I or type II. Figure 18 illustrates this procedure.
Using double integration to find area
If we integrate the constant function \(f(x, y) = 1\) over a region \(D\), we get the area of \(D\): \[ \iint_D 1 dA = A(D) \tag{10} \]
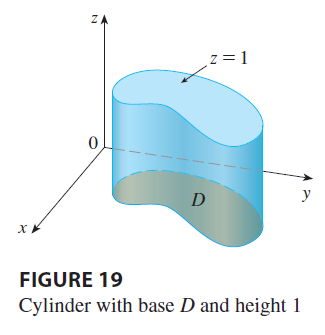
Figure 19 illustrates why Equation 10 is true: A solid cylinder whose base is \(D\) and whose height is 1 has volume \(A(D) \cdot 1 = A(D)\), but we know that we can also write its volume as \(\iint_D 1 dA\).
Lower and upper bounds on integration
If \(m \le f(x, y) \le M\) for all \((x, y) \text{ in } D\) , then
\[ mA(D) \le \iint_D f(x, y) dA \le MA(D) \tag{11} \]
EXAMPLE 6 Use Property 11 to estimate the integral \(\iint_D e^{\sin x \cos y} dA\), where \(D\) is the disk with center the origin and radius 2.
Exercise 1
Evaluate the iterated integral \(\int_0^3 \int_0^1 (8x - 2y) dy dx\).
Exercise 2
Evaluate the iterated integral \(\int_0^2 \int_0^4 x^2y dx dy\).
Exercise 3
Evaluate the iterated integral \(\int_0^1 \int_0^1 xe^{y^2} dx dy\).
Exercise 4
Evaluate the iterated integral \(\int_0^{\pi/2} \int_0^{1/2} x \sin y dy dx\).
Exercise 5
Evaluate the iterated integral \(\int_0^1 \int_0^1 \cos(s^3) dt ds\).
Exercise 6
Evaluate the iterated integral \(\int_0^1 \int_0^1 \sqrt{1 + e^v} dw dv\).
Exercise 7
Evaluate the double integral \(\iint_D \frac{y}{x^2 + 1} dA\), where \(D = \{(x, y) | 0 \le x \le 4, 0 \le y \le \sqrt{x}\}\).
Exercise 8
Evaluate the double integral \(\iint_D (2x + y) dA\), where \(D = \{(x, y) | 1 \le y \le 2, y - 1 \le x \le 1\}\).
Exercise 9
Evaluate the double integral \(\iint_D e^{-y^2} dA\), where \(D = \{(x, y) | 0 \le y \le 3, 0 \le x \le y\}\).
Exercise 10
Evaluate the double integral \(\iint_D y\sqrt{x^2 - y^2} dA\), where \(D = \{(x, y) | 0 \le x \le 2, 0 \le y \le x\}\).
Exercise 11
Draw an example of a region that is (a) type I but not type II (b) type II but not type I
Exercise 12
Draw an example of a region that is (a) both type I and type II (b) neither type I nor type II
Exercise 13
Express \(D\) as a region of type I and also as a region of type II. Then evaluate the double integral \(\iint_D x dA\) in two ways, where \(D\) is enclosed by the lines \(y = x, y = 0, x = 1\).
Exercise 14
Express \(D\) as a region of type I and also as a region of type II. Then evaluate the double integral \(\iint_D xy dA\) in two ways, where \(D\) is enclosed by the curves \(y = \sqrt{x}, y = 3x\).
Exercise 15
Set up iterated integrals for both orders of integration. Then evaluate the double integral \(\iint_D y dA\) using the easier order and explain why it’s easier, where \(D\) is bounded by \(y = x - 2, x = y^2\).
Exercise 16
Set up iterated integrals for both orders of integration. Then evaluate the double integral \(\iint_D y^2e^{xy} dA\) using the easier order and explain why it’s easier, where \(D\) is bounded by \(y = x, y = 4, x = 0\).
Exercise 17
Evaluate the double integral \(\iint_D x \cos y dA\), where \(D\) is bounded by \(y = 0, y = x^2, x = 1\).
Exercise 18
Evaluate the double integral \(\iint_D (x^2 + 2y) dA\), where \(D\) is bounded by \(y = x, y = x^3, x \ge 0\).
Exercise 19
Evaluate the double integral \(\iint_D y^2 dA\), where \(D\) is the triangular region with vertices \((0, 1), (1, 2), (4, 1)\).
Exercise 20
Evaluate the double integral \(\iint_D xy dA\), where \(D\) is enclosed by the quarter-circle \(y = \sqrt{1 - x^2}, x \ge 0\), and the axes.
Exercise 21
Evaluate the double integral \(\iint_D (2x - y) dA\), where \(D\) is bounded by the circle with center the origin and radius 2.
Exercise 22
Evaluate the double integral \(\iint_D y dA\), where \(D\) is the triangular region with vertices \((0, 0), (1, 1),\) and \((4, 0)\).
Exercise 23
Find the volume of the solid under the plane \(3x + 2y - z = 0\) and above the region enclosed by the parabolas \(y = x^2\) and \(x = y^2\).
Exercise 24
Find the volume of the solid under the surface \(z = 1 + x^2y^2\) and above the region enclosed by \(x = y^2\) and \(x = 4\).
Exercise 25
Find the volume of the solid under the surface \(z = xy\) and above the triangle with vertices \((1, 1), (4, 1),\) and \((1, 2)\).
Exercise 26
Find the volume of the solid enclosed by the paraboloid \(z = x^2 + y^2 + 1\) and the planes \(x = 0, y = 0, z = 0,\) and \(x + y = 2\).
Exercise 27
Find the volume of the tetrahedron enclosed by the coordinate planes and the plane \(2x + y + z = 4\).
Exercise 28
Find the volume of the solid bounded by the planes \(z = x, y = x, x + y = 2,\) and \(z = 0\).
Exercise 29
Find the volume of the solid enclosed by the cylinders \(z = x^2, y = x^2\) and the planes \(z = 0, y = 4\).
Exercise 30
Find the volume of the solid bounded by the cylinder \(y^2 + z^2 = 4\) and the planes \(x = 2y, x = 0, z = 0\) in the first octant.
Exercise 31
Find the volume of the solid bounded by the cylinder \(x^2 + y^2 = 1\) and the planes \(y = z, x = 0, z = 0\) in the first octant.
Exercise 32
Find the volume of the solid bounded by the cylinders \(x^2 + y^2 = r^2\) and \(y^2 + z^2 = r^2\).
Exercise 33
Use a graphing calculator or computer to estimate the x-coordinates of the points of intersection of the curves \(y = x^4\) and \(y = 3x - x^2\). If \(D\) is the region bounded by these curves, estimate \(\iint_D x dA\).
Exercise 34
Find the approximate volume of the solid in the first octant that is bounded by the planes \(y = x, z = 0,\) and \(z = x\) and the cylinder \(y = \cos x\). (Use a graphing device to estimate the points of intersection.)
Exercise 35
Find the volume of the solid by subtracting two volumes. The solid enclosed by the parabolic cylinders \(y = 1 - x^2, y = x^2 - 1\) and the planes \(x + y + z = 2, 2x + 2y - z + 10 = 0\).
Exercise 36
Find the volume of the solid by subtracting two volumes. The solid enclosed by the parabolic cylinder \(y = x^2\) and the planes \(z = 3y, z = 2 + y\).
Exercise 37
Find the volume of the solid by subtracting two volumes. The solid under the plane \(z = 3\), above the plane \(z = y\), and between the parabolic cylinders \(y = x^2\) and \(y = 1 - x^2\).
Exercise 38
Find the volume of the solid by subtracting two volumes. The solid in the first octant under the plane \(z = x + y\), above the surface \(z = xy\), and enclosed by the surfaces \(x = 0, y = 0,\) and \(x^2 + y^2 = 4\).
Exercise 39
Sketch the solid whose volume is given by the iterated integral \(\int_0^1 \int_0^{1-x} (1 - x - y) dy dx\).
Exercise 40
Sketch the solid whose volume is given by the iterated integral \(\int_0^1 \int_0^{1-x^2} (1 - x) dy dx\).
Exercise 41
Use a computer algebra system to find the exact volume of the solid under the surface \(z = x^3y^4 + xy^2\) and above the region bounded by the curves \(y = x^3 - x\) and \(y = x^2 + x\) for \(x \ge 0\).
Exercise 42
Use a computer algebra system to find the exact volume of the solid between the paraboloids \(z = 2x^2 + y^2\) and \(z = 8 - x^2 - 2y^2\) and inside the cylinder \(x^2 + y^2 = 1\).
Exercise 43
Use a computer algebra system to find the exact volume of the solid enclosed by \(z = 1 - x^2 - y^2\) and \(z = 0\).
Exercise 44
Use a computer algebra system to find the exact volume of the solid enclosed by \(z = x^2 + y^2\) and \(z = 2y\).
Exercise 45
Sketch the region of integration and change the order of integration. \(\int_0^4 \int_0^{\sqrt{x}} f(x, y) dy dx\).
Exercise 46
Sketch the region of integration and change the order of integration. \(\int_0^1 \int_{x^2}^1 f(x, y) dy dx\).
Exercise 47
Sketch the region of integration and change the order of integration. \(\int_0^{\pi/2} \int_0^{\cos x} f(x, y) dy dx\).
Exercise 48
Sketch the region of integration and change the order of integration. \(\int_{-2}^2 \int_0^{\sqrt{4-y^2}} f(x, y) dx dy\).
Exercise 49
Sketch the region of integration and change the order of integration. \(\int_1^2 \int_0^{\ln x} f(x, y) dy dx\).
Exercise 50
Sketch the region of integration and change the order of integration. \(\int_0^1 \int_{\arctan x}^{\pi/4} f(x, y) dy dx\).
Exercise 51
Evaluate the integral by reversing the order of integration. \(\int_0^1 \int_{3y}^3 e^{x^2} dx dy\).
Exercise 52
Evaluate the integral by reversing the order of integration. \(\int_0^1 \int_{\sqrt{y}}^1 \sqrt{x^3 + 1} dx dy\).
Exercise 53
Evaluate the integral by reversing the order of integration. \(\int_0^3 \int_{y^2}^9 y \cos(x^2) dx dy\).
Exercise 54
Evaluate the integral by reversing the order of integration. \(\int_0^1 \int_{\arcsin y}^{\pi/2} \cos x \sqrt{1 + \cos^2 x} dx dy\).
Exercise 55
Evaluate the integral by reversing the order of integration. \(\int_0^8 \int_{\sqrt[3]{y}}^2 e^{x^4} dx dy\).
Exercise 56
Evaluate the integral by reversing the order of integration. \(\int_0^1 \int_x^1 e^{y^2} dy dx\).
Exercise 57
Express \(D\) as a union of regions of type I or type II and evaluate the integral \(\iint_D x^2 dA\).
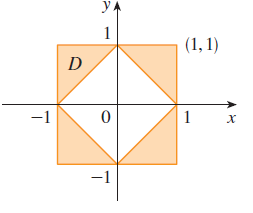
Exercise 58
Express \(D\) as a union of regions of type I or type II and evaluate the integral \(\iint_D y dA\).
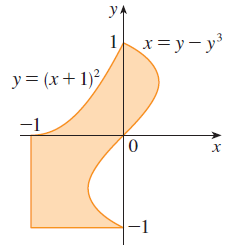
Exercise 59
Use Property 11 to estimate the value of the integral \(\iint_S \sqrt{4 - x^2y^2} dA\), where \(S = \{(x, y) | x^2 + y^2 \le 1, x \ge 0\}\).
Exercise 60
Use Property 11 to estimate the value of the integral \(\iint_T \sin^4(x + y) dA\), where \(T\) is the triangle enclosed by the lines \(y = 0, y = 2x,\) and \(x = 1\).
Exercise 61
Find the average value of \(f(x, y) = xy\) over the region \(D\), where \(D\) is the triangle with vertices \((0, 0), (1, 0),\) and \((1, 3)\).
Exercise 62
Find the average value of \(f(x, y) = x \sin y\) over the region \(D\), where \(D\) is enclosed by the curves \(y = 0, y = x^2,\) and \(x = 1\).
Exercise 63
Prove Property 11.
Exercise 64
In evaluating a double integral over a region \(D\), a sum of iterated integrals was obtained as follows: \(\iint_D f(x, y) dA = \int_0^1 \int_0^{2y} f(x, y) dx dy + \int_1^3 \int_0^{3-y} f(x, y) dx dy\). Sketch the region \(D\) and express the double integral as an iterated integral with reversed order of integration.
Exercise 65
Use geometry or symmetry, or both, to evaluate the double integral \(\iint_D (x + 2) dA\), where \(D = \{(x, y) | 0 \le y \le \sqrt{9 - x^2}\}\).
Exercise 66
Use geometry or symmetry, or both, to evaluate the double integral \(\iint_D \sqrt{R^2 - x^2 - y^2} dA\), where \(D\) is the disk with center the origin and radius \(R\).
Exercise 67
Use geometry or symmetry, or both, to evaluate the double integral \(\iint_D (2x + 3y) dA\), where \(D\) is the rectangle \(0 \le x \le a, 0 \le y \le b\).
Exercise 68
Use geometry or symmetry, or both, to evaluate the double integral \(\iint_D (2 + x^2y^3 - y^2\sin x) dA\), where \(D = \{(x, y) | |x| + |y| \le 1\}\).
Exercise 69
Use geometry or symmetry, or both, to evaluate the double integral \(\iint_D (ax^3 + by^3 + \sqrt{a^2 - x^2}) dA\), where \(D = [-a, a] \times [-b, b]\).
Exercise 70
Graph the solid bounded by the plane \(x + y + z = 1\) and the paraboloid \(z = 4 - x^2 - y^2\) and find its exact volume. (Use your CAS to do the graphing, to find the equations of the boundary curves of the region of integration, and to evaluate the double integral.)