Section 15.3: Integration in Polar Coordinates
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 15.3: Integration in Polar Coordinates |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 3:57 AM |
Table of contents
- Polar Coordinates Review
- Change to Polar Coodinates in a Double Integral
- Example: Integration in polar coordinates
- Example: Integration as volume under graph
- Polar coordinates in non-trival region
- Example
- Example
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
Polar Coordinates Review
Suppose that we want to evaluate a double integral \(\iint_R f(x, y) dA\), where \(R\) is one of the regions shown in Figure 1.
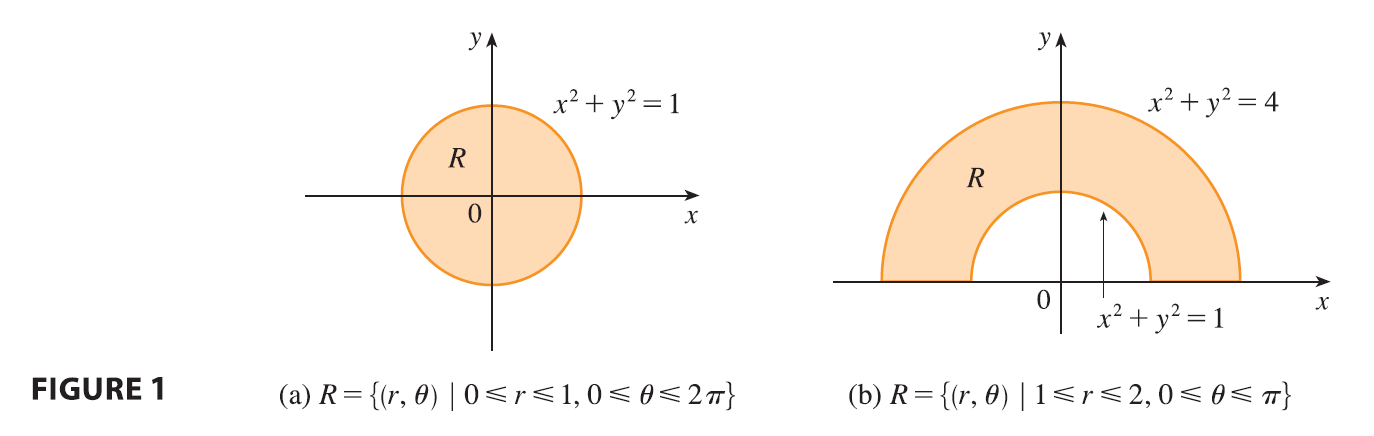
In either case the description of \(R\) in terms of rectangular coordinates is rather complicated, but \(R\) is easily described using polar coordinates.
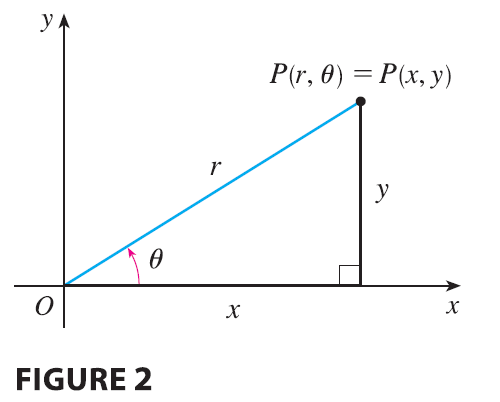
Recall from Figur2 that the polar coordinates \((r, \theta)\) of a point are related to the rectangular coordinates \((x, y)\) by the equations \[ r^2 = x^2 + y^2 \quad x = r \cos \theta \quad y = r \sin \theta \]
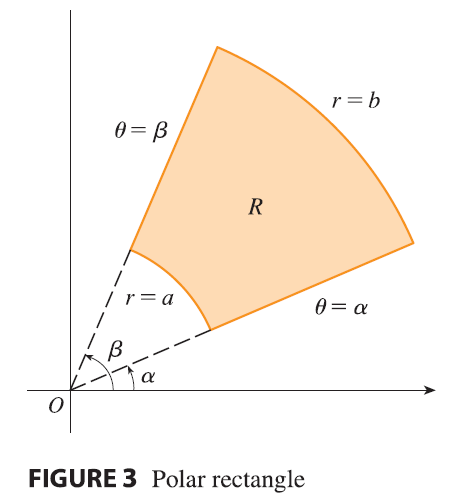
The regions in Figure 1 are special cases of a polar rectangle \[ R = \{(r, \theta) | a \le r \le b, \alpha \le \theta \le \beta\} \] which is shown in Figure 3.
Change to Polar Coodinates in a Double Integral
If \(f\) is continuous on a polar rectangle \(R\) given by \(0 \le a \le r \le b, \alpha \le \theta \le \beta\), where \(0 \le \beta - \alpha \le 2\pi\), then \[ \iint_R f(x, y) dA = \int_\alpha^\beta \int_a^b f(r \cos \theta, r \sin \theta) r dr d\theta \tag{2} \]
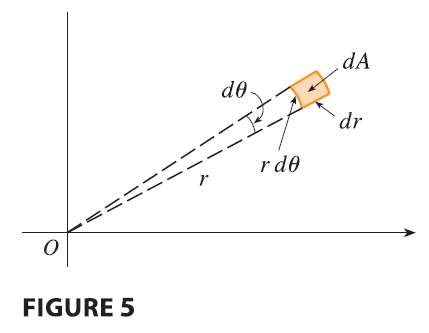
The formula in (2) says that we convert from rectangular to polar coordinates in a double integral by writing \(x = r \cos \theta\) and \(y = r \sin \theta\), using the appropriate limits of integration for \(r\) and \(\theta\), and replacing \(dA\) by \(r dr d\theta\). Be careful not to forget the additional factor \(r\) on the right side of Formula 2. A classical method for remembering this is shown in Figure 5, where the “infinitesimal” polar rectangle can be thought of as an ordinary rectangle with dimensions \(r d\theta\) and \(dr\) and therefore has “area” \(dA = r dr d\theta\).
Example: Integration in polar coordinates
EXAMPLE 1 Evaluate \(\iint_R (3x + 4y^2) dA\), where \(R\) is the region in the upper half-plane bounded by the circles \(x^2 + y^2 = 1\) and \(x^2 + y^2 = 4\).
Example: Integration as volume under graph
EXAMPLE 2 Find the volume of the solid bounded by the plane \(z = 0\) and the paraboloid \(z = 1 - x^2 - y^2\).
Polar coordinates in non-trival region
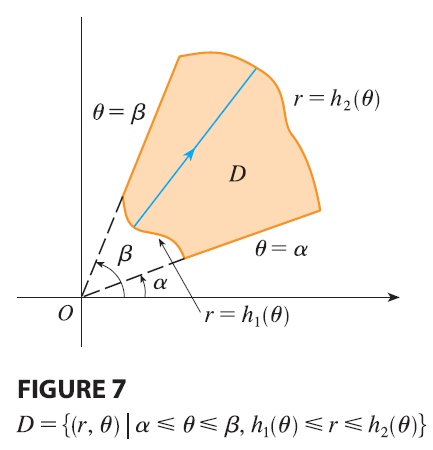
What we have done so far can be extended to the more complicated type of region shown in Figure 7. It’s similar to the type II rectangular regions considered in Section 15.2. In fact, by combining Formula 2 in this section with Formula 15.2.5, we obtain the following formula.
| If \(f\) is continuous on a polar region of the form \[ D = \{(r, \theta) | \alpha \le \theta \le \beta, h_1(\theta) \le r \le h_2(\theta)\} \] then \[ \iint_D f(x, y) dA = \int_\alpha^\beta \int_{h_1(\theta)}^{h_2(\theta)} f(r \cos \theta, r \sin \theta) r dr d\theta \tag{3} \] |
In particular, taking \(f(x, y) = 1, h_1(\theta) = 0,\) and \(h_2(\theta) = h(\theta)\) in this formula, we see that the area of the region \(D\) bounded by \(\theta = \alpha, \theta = \beta,\) and \(r = h(\theta)\) is \[ A(D) = \iint_D 1 dA = \int_\alpha^\beta \int_0^{h(\theta)} r dr d\theta = \int_\alpha^\beta \left[ \frac{r^2}{2} \right]_0^{h(\theta)} d\theta = \int_\alpha^\beta \frac{1}{2}[h(\theta)]^2 d\theta \] and this agrees with Formula 10.4.3.
Example
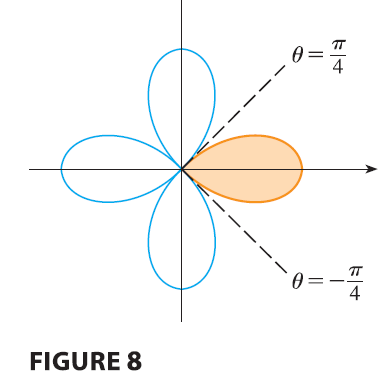
EXAMPLE 3 Use a double integral to find the area enclosed by one loop of the four-leaved rose \(r = \cos 2\theta\).
Example
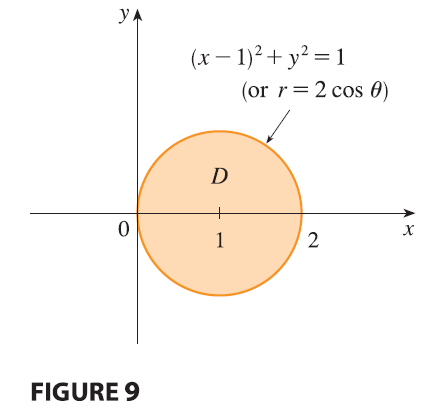
EXAMPLE 4 Find the volume of the solid that lies under the paraboloid \(z = x^2 + y^2\), above the \(xy\)-plane, and inside the cylinder \(x^2 + y^2 = 2x\).
Exercise 1
A region R is shown. Decide whether to use polar coordinates or rectangular coordinates and write \(\iint_R f(x, y) dA\) as an iterated integral, where \(f\) is an arbitrary continuous function on R.
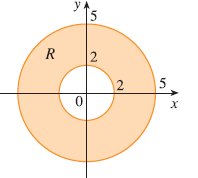
Exercise 2
A region R is shown. Decide whether to use polar coordinates or rectangular coordinates and write \(\iint_R f(x, y) dA\) as an iterated integral, where \(f\) is an arbitrary continuous function on R.
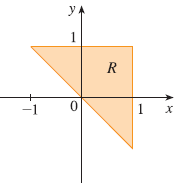
Exercise 3
A region R is shown. Decide whether to use polar coordinates or rectangular coordinates and write \(\iint_R f(x, y) dA\) as an iterated integral, where \(f\) is an arbitrary continuous function on R.
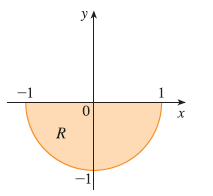
Exercise 4
A region R is shown. Decide whether to use polar coordinates or rectangular coordinates and write \(\iint_R f(x, y) dA\) as an iterated integral, where \(f\) is an arbitrary continuous function on R.
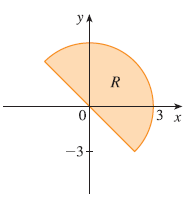
Exercise 5
Sketch the region whose area is given by the integral \(\int_{\pi/4}^{3\pi/4} \int_1^2 r dr d\theta\) and evaluate the integral.
Exercise 6
Sketch the region whose area is given by the integral \(\int_{\pi/2}^{\pi} \int_0^{2\sin\theta} r dr d\theta\) and evaluate the integral.
Exercise 7
Evaluate the given integral by changing to polar coordinates: \(\iint_D x^2y dA\), where \(D\) is the top half of the disk with center the origin and radius 5.
Exercise 8
Evaluate the given integral by changing to polar coordinates: \(\iint_R (2x - y) dA\), where \(R\) is the region in the first quadrant enclosed by the circle \(x^2 + y^2 = 4\) and the lines \(x = 0\) and \(y = x\).
Exercise 9
Evaluate the given integral by changing to polar coordinates: \(\iint_R \sin(x^2 + y^2) dA\), where \(R\) is the region in the first quadrant between the circles with center the origin and radii 1 and 3.
Exercise 10
Evaluate the given integral by changing to polar coordinates: \(\iint_R \frac{y^2}{x^2 + y^2} dA\), where \(R\) is the region that lies between the circles \(x^2 + y^2 = a^2\) and \(x^2 + y^2 = b^2\) with \(0 < a < b\).
Exercise 11
Evaluate the given integral by changing to polar coordinates: \(\iint_D e^{-x^2-y^2} dA\), where \(D\) is the region bounded by the semicircle \(x = \sqrt{4 - y^2}\) and the y-axis.
Exercise 12
Evaluate the given integral by changing to polar coordinates: \(\iint_D \cos\sqrt{x^2 + y^2} dA\), where \(D\) is the disk with center the origin and radius 2.
Exercise 13
Evaluate the given integral by changing to polar coordinates: \(\iint_R \arctan(y/x) dA\), where \(R = \{(x, y) | 1 \le x^2 + y^2 \le 4, 0 \le y \le x\}\).
Exercise 14
Evaluate the given integral by changing to polar coordinates: \(\iint_D x dA\), where \(D\) is the region in the first quadrant that lies between the circles \(x^2 + y^2 = 4\) and \(x^2 + y^2 = 2x\).
Exercise 15
Use a double integral to find the area of the region. One loop of the rose \(r = \cos 3\theta\).
Exercise 16
Use a double integral to find the area of the region enclosed by both of the cardioids \(r = 1 + \cos\theta\) and \(r = 1 - \cos\theta\).
Exercise 17
Use a double integral to find the area of the region inside the circle \((x - 1)^2 + y^2 = 1\) and outside the circle \(x^2 + y^2 = 1\).
Exercise 18
Use a double integral to find the area of the region inside the cardioid \(r = 1 + \cos\theta\) and outside the circle \(r = 3 \cos\theta\).
Exercise 19
Use polar coordinates to find the volume of the solid under the paraboloid \(z = x^2 + y^2\) and above the disk \(x^2 + y^2 \le 25\).
Exercise 20
Use polar coordinates to find the volume of the solid below the cone \(z = \sqrt{x^2 + y^2}\) and above the ring \(1 \le x^2 + y^2 \le 4\).
Exercise 21
Use polar coordinates to find the volume of the solid below the plane \(2x + y + z = 4\) and above the disk \(x^2 + y^2 \le 1\).
Exercise 22
Use polar coordinates to find the volume of the solid inside the sphere \(x^2 + y^2 + z^2 = 16\) and outside the cylinder \(x^2 + y^2 = 4\).
Exercise 23
Use polar coordinates to find the volume of a sphere of radius \(a\).
Exercise 24
Use polar coordinates to find the volume of the solid bounded by the paraboloid \(z = 1 + 2x^2 + 2y^2\) and the plane \(z = 7\) in the first octant.
Exercise 25
Use polar coordinates to find the volume of the solid above the cone \(z = \sqrt{x^2 + y^2}\) and below the sphere \(x^2 + y^2 + z^2 = 1\).
Exercise 26
Use polar coordinates to find the volume of the solid bounded by the paraboloids \(z = 6 - x^2 - y^2\) and \(z = 2x^2 + 2y^2\).
Exercise 27
Use polar coordinates to find the volume of the solid inside both the cylinder \(x^2 + y^2 = 4\) and the ellipsoid \(4x^2 + 4y^2 + z^2 = 64\).
Exercise 28
- A cylindrical drill with radius \(r_1\) is used to bore a hole through the center of a sphere of radius \(r_2\). Find the volume of the ring-shaped solid that remains.
- Express the volume in part (a) in terms of the height \(h\) of the ring. Notice that the volume depends only on \(h\), not on \(r_1\) or \(r_2\).
Exercise 29
Evaluate the iterated integral by converting to polar coordinates: \(\int_{-2}^2 \int_0^{\sqrt{4-x^2}} e^{-x^2-y^2} dy dx\).
Exercise 30
Evaluate the iterated integral by converting to polar coordinates: \(\int_0^a \int_{-\sqrt{a^2-y^2}}^{\sqrt{a^2-y^2}} (2x + y) dx dy\).
Exercise 31
Evaluate the iterated integral by converting to polar coordinates: \(\int_0^{1/2} \int_{\sqrt{3}y}^{\sqrt{1-y^2}} xy^2 dx dy\).
Exercise 32
Evaluate the iterated integral by converting to polar coordinates: \(\int_0^2 \int_0^{\sqrt{2x-x^2}} \sqrt{x^2 + y^2} dy dx\).
Exercise 33
Express the double integral \(\iint_D e^{(x^2+y^2)^2} dA\) in terms of a single integral with respect to \(r\), where \(D\) is the disk with center the origin and radius 1. Then use your calculator to evaluate the integral correct to four decimal places.
Exercise 34
Express the double integral \(\iint_D xy\sqrt{1 + x^2 + y^2} dA\) in terms of a single integral with respect to \(r\), where \(D\) is the portion of the disk \(x^2 + y^2 \le 1\) that lies in the first quadrant. Then use your calculator to evaluate the integral correct to four decimal places.
Exercise 35
A swimming pool is circular with a 40-ft diameter. The depth is constant along east-west lines and increases linearly from 2 ft at the south end to 7 ft at the north end. Find the volume of water in the pool.
Exercise 36
An agricultural sprinkler distributes water in a circular pattern of radius 100 ft. It supplies water to a depth of \(e^{-r}\) feet per hour at a distance of \(r\) feet from the sprinkler. (a) If \(0 < R \le 100\), what is the total amount of water supplied per hour to the region inside the circle of radius \(R\) centered at the sprinkler? (b) Determine an expression for the average amount of water per hour per square foot supplied to the region inside the circle of radius \(R\).
Exercise 37
Find the average value of the function \(f(x, y) = 1/\sqrt{x^2 + y^2}\) on the annular region \(a^2 \le x^2 + y^2 \le b^2\), where \(0 < a < b\).
Exercise 38
Let \(D\) be the disk with center the origin and radius \(a\). What is the average distance from points in \(D\) to the origin?
Exercise 39
Use polar coordinates to combine the sum \[ \int_{1/\sqrt{2}}^1 \int_{\sqrt{1-x^2}}^x xy dy dx + \int_1^{\sqrt{2}} \int_0^x xy dy dx + \int_{\sqrt{2}}^2 \int_0^{\sqrt{4-x^2}} xy dy dx \] into one double integral. Then evaluate the double integral.
Exercise 40
- We define the improper integral (over the entire plane \(\mathbb{R}^2\)) \(I = \iint_{\mathbb{R}^2} e^{-(x^2+y^2)} dA = \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-(x^2+y^2)} dy dx = \lim_{a \to \infty} \iint_{D_a} e^{-(x^2+y^2)} dA\) where \(D_a\) is the disk with radius \(a\) and center the origin. Show that \(\int_{-\infty}^\infty \int_{-\infty}^\infty e^{-(x^2+y^2)} dA = \pi\).
- An equivalent definition of the improper integral in part (a) is \(\iint_{\mathbb{R}^2} e^{-(x^2+y^2)} dA = \lim_{a \to \infty} \iint_{S_a} e^{-(x^2+y^2)} dA\) where \(S_a\) is the square with vertices \((\pm a, \pm a)\). Use this to show that \(\int_{-\infty}^\infty e^{-x^2} dx \int_{-\infty}^\infty e^{-y^2} dy = \pi\).
- Deduce that \[ \int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi}. \]
- By making the change of variable \(t = \sqrt{2}x\), show that \(\int_{-\infty}^\infty e^{-x^2/2} dx = \sqrt{2\pi}\). (This is a fundamental result for probability and statistics.)
Exercise 41
Use the result of Exercise 40 part (c) to evaluate the following integrals. (a) \(\int_0^\infty x^2e^{-x^2} dx\) (b) \(\int_0^\infty \sqrt{x}e^{-x} dx\)