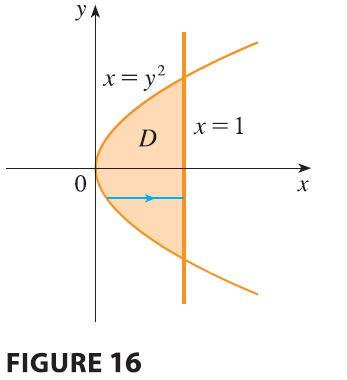Section 15.6: Triple Integration
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 15.6: Triple Integration |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 2:12 AM |
Table of contents
- Triple Integrals - Integration over volume
- Working Rule - Fubini’s Theorem for Triple Integrals
- Example - Triple Integration
- Theory: Triple Integration over general region
- Example
- Type 2 - volume
- Type 3 volume
- Example
- Example
- Applications of Triple Integrals
- Example
- Other Applications of Triple integrations
- Example
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
- Exercise 49
- Exercise 50
- Exercise 51
- Exercise 52
- Exercise 53
- Exercise 54
- Exercise 55
Triple Integrals - Integration over volume
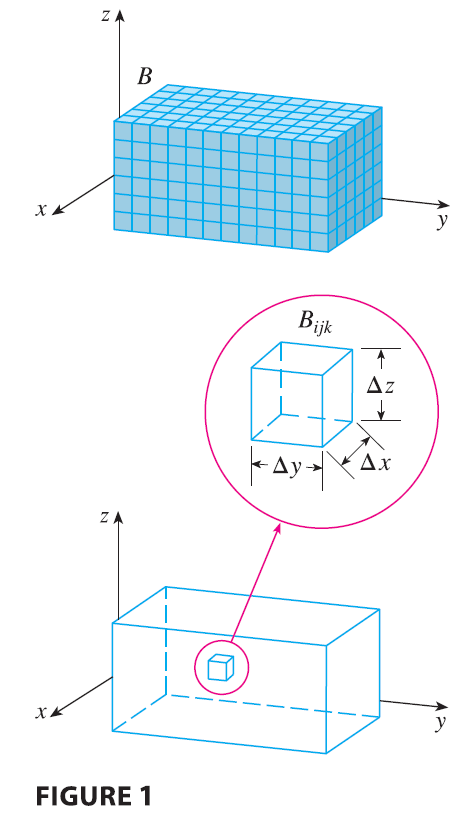
Just as we defined single integrals for functions of one variable and double integrals for functions of two variables, so we can define triple integrals for functions of three variables. Let’s first deal with the simplest case where \(f\) is defined on a rectangular box: \[ B = \{(x, y, z) | a \le x \le b, c \le y \le d, r \le z \le s\} \tag{1} \] The first step is to divide \(B\) into sub-boxes. We do this by dividing the interval \([a, b]\) into \(l\) subintervals \([x_{i-1}, x_i]\) of equal width \(\Delta x\), dividing \([c, d]\) into \(m\) subintervals of width \(\Delta y\), and dividing \([r, s]\) into \(n\) subintervals of width \(\Delta z\). The planes through the endpoints of these subintervals parallel to the coordinate planes divide the box \(B\) into \(lmn\) sub-boxes \[ B_{ijk} = [x_{i-1}, x_i] \times [y_{j-1}, y_j] \times [z_{k-1}, z_k] \] which are shown in Figure 1. Each sub-box has volume \(\Delta V = \Delta x \Delta y \Delta z\).
Then we form the triple Riemann sum \[ \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*) \Delta V \tag{2} \] where the sample point \((x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\) is in \(B_{ijk}\). By analogy with the definition of a double integral (15.1.5), we define the triple integral as the limit of the triple Riemann sums in (2).
Definition 3 The triple integral of \(f\) over the box \(B\) is \[ \iiint_B f(x, y, z) dV = \lim_{l,m,n \to \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*) \Delta V \] if this limit exists.
Again, the triple integral always exists if \(f\) is continuous. We can choose the sample point to be any point in the sub-box, but if we choose it to be the point \((x_i, y_j, z_k)\) we get a simpler-looking expression for the triple integral: \[ \iiint_B f(x, y, z) dV = \lim_{l,m,n \to \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(x_i, y_j, z_k) \Delta V \] Just as for double integrals, the practical method for evaluating triple integrals is to express them as iterated integrals as follows.
Working Rule - Fubini’s Theorem for Triple Integrals
If \(f\) is continuous on the rectangular box \(B = [a, b] \times [c, d] \times [r, s]\), then \[ \iiint_B f(x, y, z) dV = \int_r^s \int_c^d \int_a^b f(x, y, z) dx dy dz \]
The iterated integral on the right side of Fubini’s Theorem means that we integrate first with respect to \(x\) (keeping \(y\) and \(z\) fixed), then we integrate with respect to \(y\) (keeping \(z\) fixed), and finally we integrate with respect to \(z\). There are five other possible orders in which we can integrate, all of which give the same value. For instance, if we integrate with respect to \(y\), then \(z\), and then \(x\), we have \[ \iiint_B f(x, y, z) dV = \int_a^b \int_r^s \int_c^d f(x, y, z) dy dz dx \]
Example - Triple Integration
EXAMPLE 1 Evaluate the triple integral \(\iiint_B xyz^2 dV\), where \(B\) is the rectangular box given by \[ B = \{(x, y, z) | 0 \le x \le 1, -1 \le y \le 2, 0 \le z \le 3\} \]
Theory: Triple Integration over general region
We define the triple integral over a general bounded region \(E\) in three-dimensional space (a solid) by much the same procedure that we used for double integrals (15.2.2). We enclose \(E\) in a box \(B\) of the type given by Equation 1. Then we define \(F\) so that it agrees with \(f\) on \(E\) but is 0 for points in \(B\) that are outside \(E\). By definition, \[ \iiint_E f(x, y, z) dV = \iiint_B F(x, y, z) dV \] This integral exists if \(f\) is continuous and the boundary of \(E\) is “reasonably smooth.” The triple integral has essentially the same properties as the double integral (Properties 6–9 in Section 15.2).
We restrict our attention to continuous functions \(f\) and to certain simple types of regions. A solid region \(E\) is said to be of type 1 if it lies between the graphs of two continuous functions of \(x\) and \(y\), that is, \[ E = \{(x, y, z) | (x, y) \in D, u_1(x, y) \le z \le u_2(x, y)\} \tag{5} \]
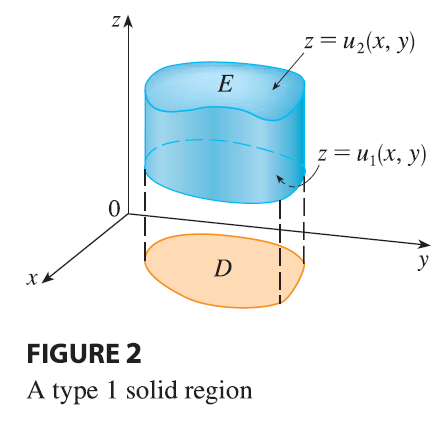
where \(D\) is the projection of \(E\) onto the \(xy\)-plane as shown in Figure 2. Notice that the upper boundary of the solid \(E\) is the surface with equation \(z = u_2(x, y)\), while the lower boundary is the surface \(z = u_1(x, y)\).
By the same sort of argument that led to (15.2.3), it can be shown that if \(E\) is a type 1 region given by Equation 5, then \[ \iiint_E f(x, y, z) dV = \iint_D \left[ \int_{u_1(x,y)}^{u_2(x,y)} f(x, y, z) dz \right] dA \tag{6} \] The meaning of the inner integral on the right side of Equation 6 is that \(x\) and \(y\) are held fixed, and therefore \(u_1(x, y)\) and \(u_2(x, y)\) are regarded as constants, while \(f(x, y, z)\) is integrated with respect to \(z\).
In particular, if the projection \(D\) of \(E\) onto the \(xy\)-plane is a type I plane region (as in Figure 3), then
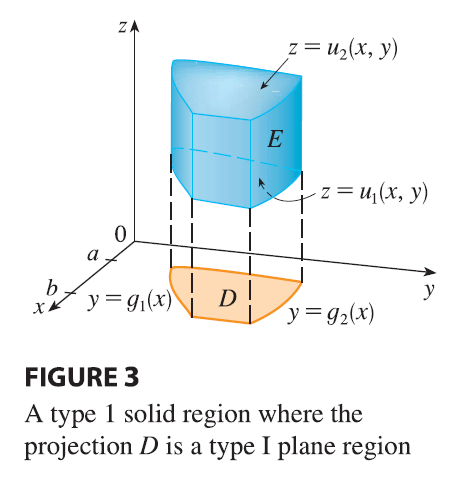
\[ E = \{(x, y, z) | a \le x \le b, g_1(x) \le y \le g_2(x), u_1(x, y) \le z \le u_2(x, y)\} \] and Equation 6 becomes \[ \iiint_E f(x, y, z) dV = \int_a^b \int_{g_1(x)}^{g_2(x)} \int_{u_1(x,y)}^{u_2(x,y)} f(x, y, z) dz dy dx \tag{7} \] If, on the other hand, \(D\) is a type II plane region (as in Figure 4), then
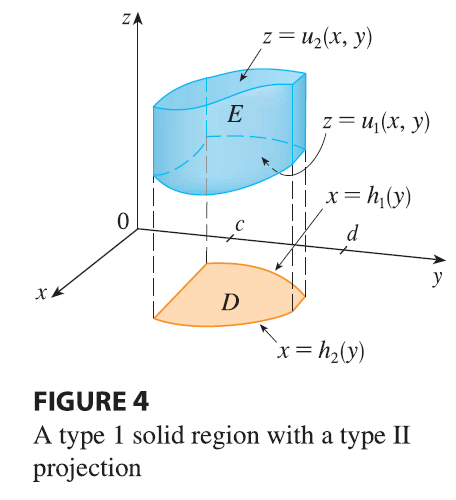
\[ E = \{(x, y, z) | c \le y \le d, h_1(y) \le x \le h_2(y), u_1(x, y) \le z \le u_2(x, y)\} \] and Equation 6 becomes \[ \iiint_E f(x, y, z) dV = \int_c^d \int_{h_1(y)}^{h_2(y)} \int_{u_1(x,y)}^{u_2(x,y)} f(x, y, z) dz dx dy \tag{8} \]
Example
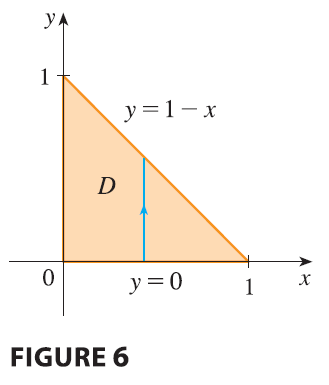
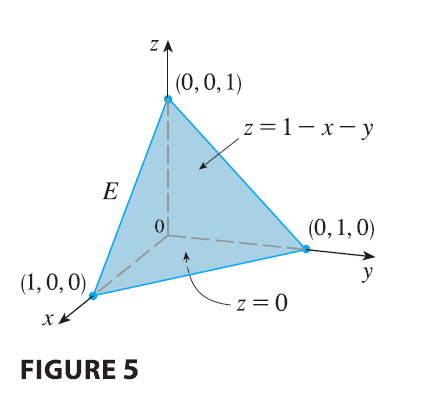
EXAMPLE 2 Evaluate \(\iiint_E z dV\), where \(E\) is the solid tetrahedron bounded by the four planes \(x = 0, y = 0, z = 0,\) and \(x + y + z = 1\).
Type 2 - volume
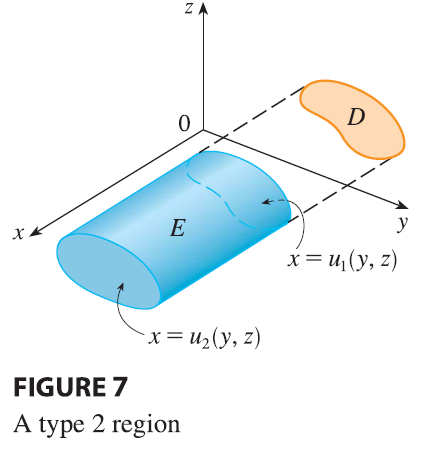
A solid region \(E\) is of type 2 if it is of the form \[ E = \{(x, y, z) | (y, z) \in D, u_1(y, z) \le x \le u_2(y, z)\} \] where, this time, \(D\) is the projection of \(E\) onto the \(yz\)-plane (see Figure 7). The back surface is \(x = u_1(y, z)\), the front surface is \(x = u_2(y, z)\), and we have \[ \iiint_E f(x, y, z) dV = \iint_D \left[ \int_{u_1(y,z)}^{u_2(y,z)} f(x, y, z) dx \right] dA \tag{10} \]
Type 3 volume
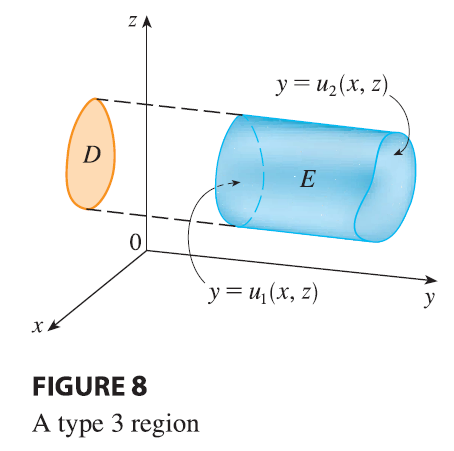
Finally, a type 3 region is of the form \[ E = \{(x, y, z) | (x, z) \in D, u_1(x, z) \le y \le u_2(x, z)\} \] where \(D\) is the projection of \(E\) onto the \(xz\)-plane, \(y = u_1(x, z)\) is the left surface, and \(y = u_2(x, z)\) is the right surface (see Figure 8). For this type of region we have \[ \iiint_E f(x, y, z) dV = \iint_D \left[ \int_{u_1(x,z)}^{u_2(x,z)} f(x, y, z) dy \right] dA \tag{11} \] In each of Equations 10 and 11 there may be two possible expressions for the integral depending on whether \(D\) is a type I or type II plane region (and corresponding to Equations 7 and 8).
Example
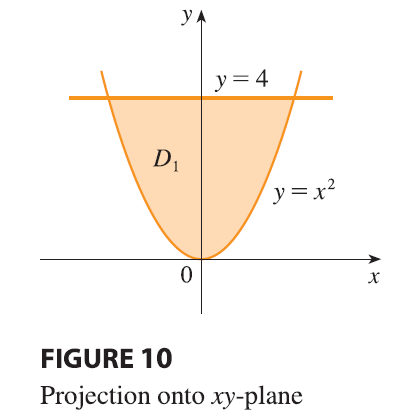
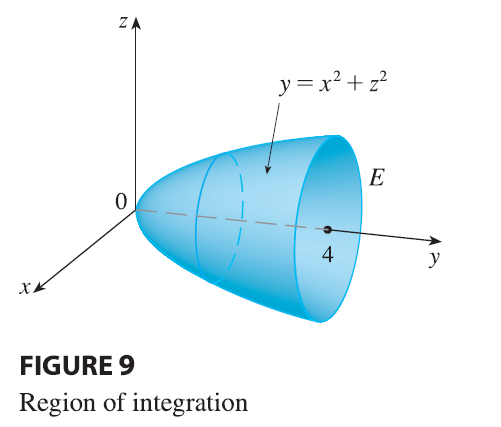
EXAMPLE 3 Evaluate \(\iiint_E \sqrt{x^2 + z^2} dV\), where \(E\) is the region bounded by the paraboloid \(y = x^2 + z^2\) and the plane \(y = 4\).
Example
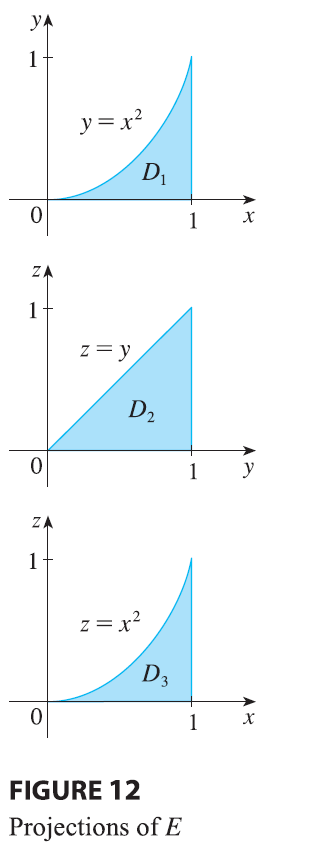
EXAMPLE 4 Express the iterated integral \(\int_0^1 \int_0^{x^2} \int_0^y f(x, y, z) dz dy dx\) as a triple integral and then rewrite it as an iterated integral in a different order, integrating first with respect to \(x\), then \(z\), and then \(y\).
Applications of Triple Integrals
Recall that if \(f(x) \ge 0\), then the single integral \(\int_a^b f(x) dx\) represents the area under the curve \(y = f(x)\) from \(a\) to \(b\), and if \(f(x, y) \ge 0\), then the double integral \(\iint_D f(x, y) dA\) represents the volume under the surface \(z = f(x, y)\) and above \(D\). The corresponding interpretation of a triple integral \(\iiint_E f(x, y, z) dV\), where \(f(x, y, z) \ge 0\), is not very useful because it would be the “hypervolume” of a four-dimensional object and, of course, that is very difficult to visualize. Nonetheless, the triple integral \(\iiint_E f(x, y, z) dV\) can be interpreted in different ways in different physical situations, depending on the physical interpretations of \(x, y, z,\) and \(f(x, y, z)\).
Let’s begin with the special case where \(f(x, y, z) = 1\) for all points in \(E\). Then the triple integral does represent the volume of \(E\): \[ V(E) = \iiint_E dV \tag{12} \] For example, you can see this in the case of a type 1 region by putting \(f(x, y, z) = 1\) in Formula 6: \[ \iiint_E 1 dV = \iint_D \left[ \int_{u_1(x,y)}^{u_2(x,y)} dz \right] dA = \iint_D [u_2(x, y) - u_1(x, y)] dA \] and from Section 15.2 we know this represents the volume that lies between the surfaces \(z = u_1(x, y)\) and \(z = u_2(x, y)\).
Example
EXAMPLE 5 Use a triple integral to find the volume of the tetrahedron \(T\) bounded by the planes \(x + 2y + z = 2, x = 2y, x = 0,\) and \(z = 0\).
Other Applications of Triple integrations
All the applications of double integrals in Section 15.4 can be immediately extended to triple integrals. For example, if the density function of a solid object that occupies the region \(E\) is \(\rho(x, y, z)\), in units of mass per unit volume, at any given point \((x, y, z)\), then its mass is \[ m = \iiint_E \rho(x, y, z) dV \tag{13} \] and its moments about the three coordinate planes are \[ M_{yz} = \iiint_E x\rho(x, y, z) dV \quad M_{xz} = \iiint_E y\rho(x, y, z) dV \tag{14} \] \[ M_{xy} = \iiint_E z\rho(x, y, z) dV \] The center of mass is located at the point \((\bar{x}, \bar{y}, \bar{z})\), where \[ \bar{x} = \frac{M_{yz}}{m} \quad \bar{y} = \frac{M_{xz}}{m} \quad \bar{z} = \frac{M_{xy}}{m} \tag{15} \] If the density is constant, the center of mass of the solid is called the centroid of \(E\). The moments of inertia about the three coordinate axes are \[ I_x = \iiint_E (y^2 + z^2)\rho(x, y, z) dV \quad I_y = \iiint_E (x^2 + z^2)\rho(x, y, z) dV \tag{16} \] \[ I_z = \iiint_E (x^2 + y^2)\rho(x, y, z) dV \] As in Section 15.4, the total electric charge on a solid object occupying a region \(E\) and having charge density \(\sigma(x, y, z)\) is \[ Q = \iiint_E \sigma(x, y, z) dV \] If we have three continuous random variables \(X, Y,\) and \(Z\), their joint density function is a function of three variables such that the probability that \((X, Y, Z)\) lies in \(E\) is \[ P((X, Y, Z) \in E) = \iiint_E f(x, y, z) dV \] In particular, \[ P(a \le X \le b, c \le Y \le d, r \le Z \le s) = \int_a^b \int_c^d \int_r^s f(x, y, z) dz dy dx \] The joint density function satisfies \[ f(x, y, z) \ge 0 \quad \int_{-\infty}^\infty \int_{-\infty}^\infty \int_{-\infty}^\infty f(x, y, z) dz dy dx = 1 \]
Example
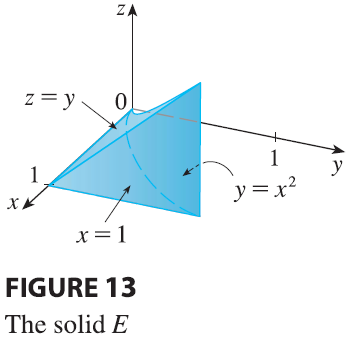
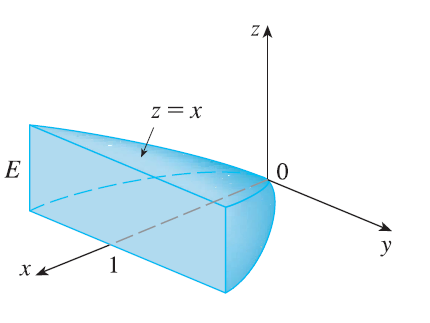
EXAMPLE 6 Find the center of mass of a solid of constant density that is bounded by the parabolic cylinder \(x = y^2\) and the planes \(x = z, z = 0,\) and \(x = 1\).
Exercise 2
Evaluate the integral \(\iiint_E (xy + z^2) dV\), where \(E = \{(x, y, z) | 0 \le x \le 2, 0 \le y \le 1, 0 \le z \le 3\}\) using three different orders of integration.
Exercise 3
Evaluate the iterated integral \(\int_0^1 \int_0^z \int_0^{x+z} (2x - y) dy dx dz\).
Exercise 4
Evaluate the iterated integral \(\int_0^1 \int_y^{2y} \int_0^{x+y} 6xy dz dx dy\).
Exercise 5
Evaluate the iterated integral \(\int_1^2 \int_0^{2z} \int_0^{\ln x} xe^{-y} dy dx dz\).
Exercise 6
Evaluate the iterated integral \(\int_0^1 \int_0^z \int_0^{\sqrt{1-z^2}} \frac{z}{y+1} dx dz dy\).
Exercise 7
Evaluate the iterated integral \(\int_0^{\pi/2} \int_0^y \int_0^x z \sin x dy dz dx\).
Exercise 8
Evaluate the iterated integral \(\int_0^{\sqrt{\pi}} \int_0^x \int_0^{xz} x^2 \sin y dy dz dx\).
Exercise 9
Evaluate the triple integral \(\iiint_E y dV\), where \(E = \{(x, y, z) | 0 \le x \le 3, 0 \le y \le x, x - y \le z \le x + y\}\).
Exercise 10
Evaluate the triple integral \(\iiint_E e^{z/y} dV\), where \(E = \{(x, y, z) | 0 \le y \le 1, y \le x \le 1, 0 \le z \le xy\}\).
Exercise 11
Evaluate the triple integral \(\iiint_E \frac{z}{x^2 + z^2} dV\), where \(E = \{(x, y, z) | 1 \le y \le 4, y \le z \le 4, 0 \le x \le z\}\).
Exercise 12
Evaluate the triple integral \(\iiint_E \sin y dV\), where E lies below the plane \(z = x\) and above the triangular region with vertices \((0, 0, 0), (\pi, 0, 0),\) and \((0, \pi, 0)\).
Exercise 13
Evaluate the triple integral \(\iiint_E 6xy dV\), where E lies under the plane \(z = 1 + x + y\) and above the region in the xy-plane bounded by the curves \(y = \sqrt{x}, y = 0,\) and \(x = 1\).
Exercise 14
Evaluate the triple integral \(\iiint_E (x - y) dV\), where E is enclosed by the surfaces \(z = x^2 - 1, z = 1 - x^2, y = 0,\) and \(y = 2\).
Exercise 15
Evaluate the triple integral \(\iiint_T xy^2 dV\), where T is the solid tetrahedron with vertices \((0, 0, 0), (2, 0, 0), (0, 2, 0),\) and \((0, 0, 2)\).
Exercise 16
Evaluate the triple integral \(\iiint_T xz dV\), where T is the solid tetrahedron with vertices \((0, 0, 0), (1, 0, 1), (0, 1, 1),\) and \((0, 0, 1)\).
Exercise 17
Evaluate the triple integral \(\iiint_E x dV\), where E is bounded by the paraboloid \(x = 4y^2 + 4z^2\) and the plane \(x = 4\).
Exercise 18
Evaluate the triple integral \(\iiint_E z dV\), where E is bounded by the cylinder \(y^2 + z^2 = 9\) and the planes \(x = 0, y = 3x,\) and \(z = 0\) in the first octant.
Exercise 19
Use a triple integral to find the volume of the tetrahedron enclosed by the coordinate planes and the plane \(2x + y + z = 4\).
Exercise 20
Use a triple integral to find the volume of the solid enclosed by the paraboloids \(y = x^2 + z^2\) and \(y = 8 - x^2 - z^2\).
Exercise 21
Use a triple integral to find the volume of the solid enclosed by the cylinder \(y = x^2\) and the planes \(z = 0\) and \(y + z = 1\).
Exercise 22
Use a triple integral to find the volume of the solid enclosed by the cylinder \(x^2 + z^2 = 4\) and the planes \(y = -1\) and \(y + z = 4\).
Exercise 23
- Express the volume of the wedge in the first octant that is cut from the cylinder \(y^2 + z^2 = 1\) by the planes \(y = x\) and \(x = 1\) as a triple integral.
- Use either the Table of Integrals or a computer algebra system to find the exact value of the triple integral in part (a).
Exercise 24
- In the Midpoint Rule for triple integrals we use a triple Riemann sum to approximate a triple integral over a box B, where \(f(x, y, z)\) is evaluated at the center \((\bar{x}_i, \bar{y}_j, \bar{z}_k)\) of the box \(B_{ijk}\). Use the Midpoint Rule to estimate \(\iiint_B \sqrt{x^2 + y^2 + z^2} dV\), where B is the cube defined by \(0 \le x \le 4, 0 \le y \le 4, 0 \le z \le 4\). Divide B into eight cubes of equal size.
- Use a computer algebra system to approximate the integral in part (a) correct to the nearest integer. Compare with the answer to part (a).
Exercise 25
Use the Midpoint Rule for triple integrals (Exercise 24) to estimate the value of the integral. Divide B into eight sub-boxes of equal size. \(\iiint_B \cos(xyz) dV\), where \(B = \{(x, y, z) | 0 \le x \le 1, 0 \le y \le 1, 0 \le z \le 1\}\).
Exercise 26
Use the Midpoint Rule for triple integrals (Exercise 24) to estimate the value of the integral. Divide B into eight sub-boxes of equal size. \(\iiint_B \sqrt{x}e^{xyz} dV\), where \(B = \{(x, y, z) | 0 \le x \le 4, 0 \le y \le 1, 0 \le z \le 2\}\).
Exercise 27
Sketch the solid whose volume is given by the iterated integral \(\int_0^1 \int_0^{1-x} \int_0^{2-2z} dy dz dx\).
Exercise 28
Sketch the solid whose volume is given by the iterated integral \(\int_0^2 \int_0^{2-y} \int_0^{4-y^2} dx dz dy\).
Exercise 29
Express the integral \(\iiint_E f(x, y, z) dV\) as an iterated integral in six different ways, where E is the solid bounded by the surfaces \(y = 4 - x^2 - 4z^2, y = 0\).
Exercise 30
Express the integral \(\iiint_E f(x, y, z) dV\) as an iterated integral in six different ways, where E is the solid bounded by the surfaces \(y^2 + z^2 = 9, x = -2, x = 2\).
Exercise 31
Express the integral \(\iiint_E f(x, y, z) dV\) as an iterated integral in six different ways, where E is the solid bounded by the surfaces \(y = x^2, z = 0, y + 2z = 4\).
Exercise 32
Express the integral \(\iiint_E f(x, y, z) dV\) as an iterated integral in six different ways, where E is the solid bounded by the surfaces \(x = 2, y = 2, z = 0, x + y - 2z = 2\).
Exercise 33
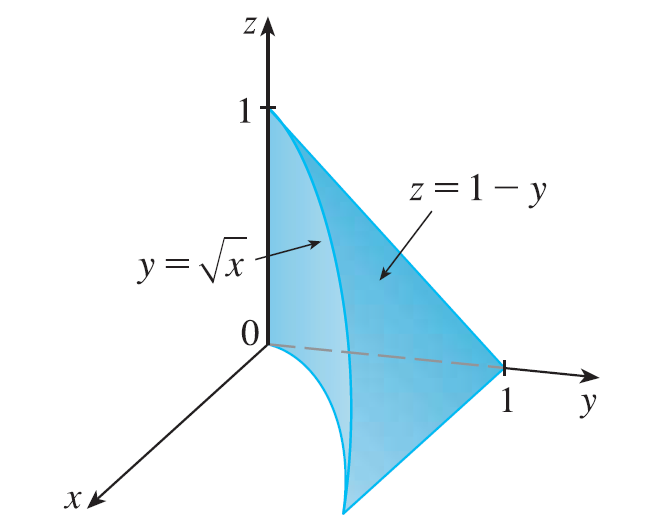
The figure shows the region of integration for the integral \(\int_0^1 \int_{\sqrt{x}}^1 \int_0^{1-y} f(x, y, z) dz dy dx\). Rewrite this integral as an equivalent iterated integral in the five other orders.
Exercise 34
The figure shows the region of integration for the integral \(\int_0^1 \int_0^{1-x^2} \int_0^{1-x} f(x, y, z) dy dz dx\). Rewrite this integral as an equivalent iterated integral in the five other orders.
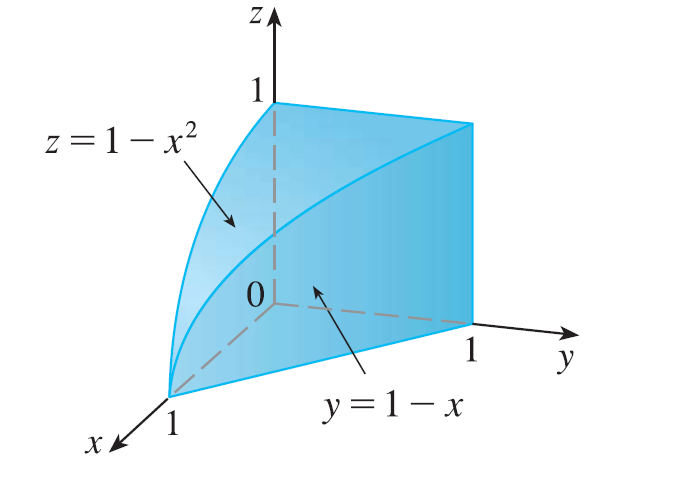
Exercise 35
Write five other iterated integrals that are equal to the given iterated integral \(\int_0^1 \int_y^1 \int_0^y f(x, y, z) dz dx dy\).
Exercise 36
Write five other iterated integrals that are equal to the given iterated integral \(\int_0^1 \int_0^{x^2} \int_0^y f(x, y, z) dz dy dx\).
Exercise 37
Evaluate the triple integral \(\iiint_C (4 + 5x^2yz^2) dV\), where C is the cylindrical region \(x^2 + y^2 \le 4, -2 \le z \le 2\), using only geometric interpretation and symmetry.
Exercise 38
Evaluate the triple integral \(\iiint_B (z^3 + \sin y + 3) dV\), where B is the unit ball \(x^2 + y^2 + z^2 \le 1\), using only geometric interpretation and symmetry.
Exercise 39
Find the mass and center of mass of the solid E with the given density function \(\rho\). E lies above the xy-plane and below the paraboloid \(z = 1 - x^2 - y^2\); \(\rho(x, y, z) = 3\).
Exercise 40
Find the mass and center of mass of the solid E with the given density function \(\rho\). E is bounded by the parabolic cylinder \(z = 1 - y^2\) and the planes \(x + z = 1, x = 0,\) and \(z = 0\); \(\rho(x, y, z) = 4\).
Exercise 41
Find the mass and center of mass of the solid E with the given density function \(\rho\). E is the cube given by \(0 \le x \le a, 0 \le y \le a, 0 \le z \le a\); \(\rho(x, y, z) = x^2 + y^2 + z^2\).
Exercise 42
Find the mass and center of mass of the solid E with the given density function \(\rho\). E is the tetrahedron bounded by the planes \(x = 0, y = 0, z = 0, x + y + z = 1\); \(\rho(x, y, z) = y\).
Exercise 43
Assume that the solid has constant density \(k\). Find the moments of inertia for a cube with side length L if one vertex is located at the origin and three edges lie along the coordinate axes.
Exercise 44
Assume that the solid has constant density \(k\). Find the moments of inertia for a rectangular brick with dimensions a, b, and c and mass M if the center of the brick is situated at the origin and the edges are parallel to the coordinate axes.
Exercise 45
Assume that the solid has constant density \(k\). Find the moment of inertia about the z-axis of the solid cylinder \(x^2 + y^2 \le a^2, 0 \le z \le h\).
Exercise 46
Assume that the solid has constant density \(k\). Find the moment of inertia about the z-axis of the solid cone \(\sqrt{x^2 + y^2} \le z \le h\).
Exercise 47
Set up, but do not evaluate, integral expressions for (a) the mass, (b) the center of mass, and (c) the moment of inertia about the z-axis. The solid of Exercise 21; \(\rho(x, y, z) = \sqrt{x^2 + y^2}\).
Exercise 48
Set up, but do not evaluate, integral expressions for (a) the mass, (b) the center of mass, and (c) the moment of inertia about the z-axis. The hemisphere \(x^2 + y^2 + z^2 \le 1, z \ge 0\); \(\rho(x, y, z) = \sqrt{x^2 + y^2 + z^2}\).
Exercise 49
Let E be the solid in the first octant bounded by the cylinder \(x^2 + y^2 = 1\) and the planes \(y = z, x = 0,\) and \(z = 0\) with the density function \(\rho(x, y, z) = 1 + x + y + z\). Use a computer algebra system to find the exact values of the following quantities for E. (a) The mass (b) The center of mass (c) The moment of inertia about the z-axis
Exercise 50
If E is the solid of Exercise 18 with density function \(\rho(x, y, z) = x^2 + y^2\), find the following quantities, correct to three decimal places. (a) The mass (b) The center of mass (c) The moment of inertia about the z-axis
Exercise 51
The joint density function for random variables X, Y, and Z is \(f(x, y, z) = Cxyz\) if \(0 \le x \le 2, 0 \le y \le 2, 0 \le z \le 2\), and \(f(x, y, z) = 0\) otherwise. (a) Find the value of the constant C. (b) Find \(P(X \le 1, Y \le 1, Z \le 1)\). (c) Find \(P(X + Y + Z \le 1)\).
Exercise 52
Suppose X, Y, and Z are random variables with joint density function \(f(x, y, z) = Ce^{-(0.5x+0.2y+0.1z)}\) if \(x \ge 0, y \ge 0, z \ge 0\), and \(f(x, y, z) = 0\) otherwise. (a) Find the value of the constant C. (b) Find \(P(X \le 1, Y \le 1)\). (c) Find \(P(X \le 1, Y \le 1, Z \le 1)\).
Exercise 53
The average value of a function \(f(x, y, z)\) over a solid region E is defined to be \(f_{ave} = \frac{1}{V(E)} \iiint_E f(x, y, z) dV\) where \(V(E)\) is the volume of E. For instance, if \(\rho\) is a density function, then \(\rho_{ave}\) is the average density of E. Find the average value of the function \(f(x, y, z) = xyz\) over the cube with side length L that lies in the first octant with one vertex at the origin and edges parallel to the coordinate axes.
Exercise 54
Find the average height of the points in the solid hemisphere \(x^2 + y^2 + z^2 \le 1, z \ge 0\).
Exercise 55
- Find the region E for which the triple integral \(\iiint_E (1 - x^2 - 2y^2 - 3z^2) dV\) is a maximum.
- Use a computer algebra system to calculate the exact maximum value of the triple integral in part (a).