Section 12.1: Three dimenstional Coordinate Geometry
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 12.1: Three dimenstional Coordinate Geometry |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 3:57 AM |
Table of contents
- 3D Space
- Surfaces
- Distance and Spheres
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
3D Space
To locate a point in a plane, we need two numbers. We know that any point in the plane can be represented as an ordered pair \((a, b)\) of real numbers, where \(a\) is the x-coordinate and \(b\) is the y-coordinate. For this reason, a plane is called two-dimensional. To locate a point in space, three numbers are required. We represent any point in space by an ordered triple \((a, b, c)\) of real numbers.
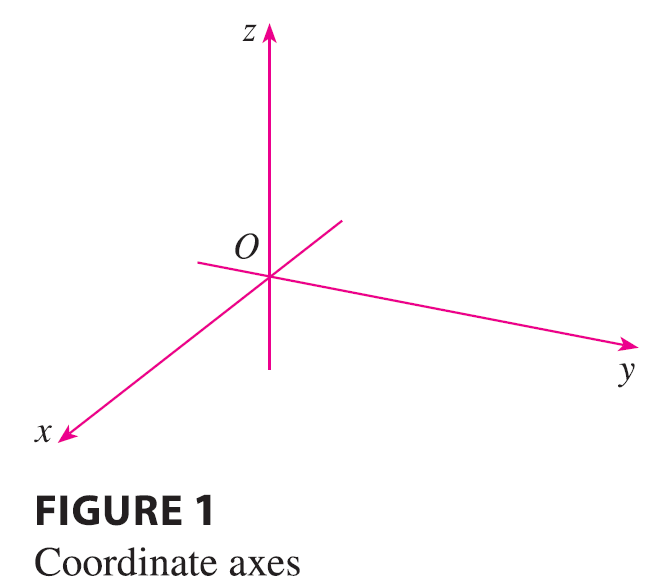
In order to represent points in space, we first choose a fixed point \(O\) (the origin) and three directed lines through \(O\) that are perpendicular to each other, called the coordinate axes and labeled the x-axis, y-axis, and z-axis. Usually we think of the x- and y-axes as being horizontal and the z-axis as being vertical, and we draw the orientation of the axes as in Figure 1.
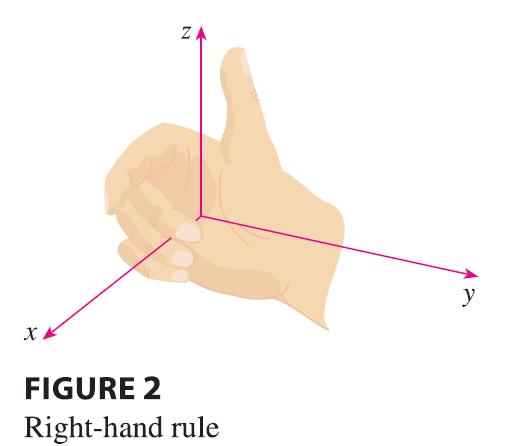
The direction of the z-axis is determined by the right-hand rule as illustrated in Figure 2: If you curl the fingers of your right hand around the z-axis in the direction of a 90° counterclockwise rotation from the positive x-axis to the positive y-axis, then your thumb points in the positive direction of the z-axis.
The three coordinate axes determine the three coordinate planes illustrated in Figure 3(a). The xy-plane is the plane that contains the x- and y-axes; the yz-plane contains the y- and z-axes; the xz-plane contains the x- and z-axes. These three coordinate planes divide space into eight parts, called octants. The first octant, in the foreground, is determined by the positive axes.
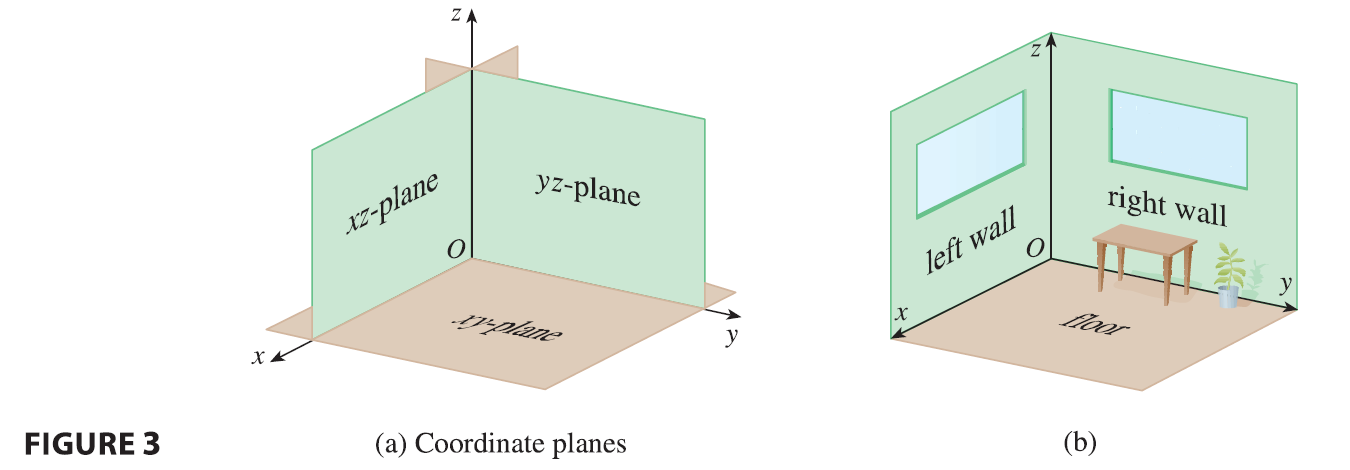
Because many people have some difficulty visualizing diagrams of three-dimensional figures, you may find it helpful to do the following [see Figure 3(b)]. Look at any bottom corner of a room and call the corner the origin. The wall on your left is in the xz-plane, the wall on your right is in the yz-plane, and the floor is in the xy-plane. The x-axis runs along the intersection of the floor and the left wall. The y-axis runs along the intersection of the floor and the right wall. The z-axis runs up from the floor toward the ceiling along the intersection of the two walls. You are situated in the first octant, and you can now imagine seven other rooms situated in the other seven octants (three on the same floor and four on the floor below), all connected by the common corner point \(O\).
Now if \(P\) is any point in space, let \(a\) be the (directed) distance from the yz-plane to \(P\), let \(b\) be the distance from the xz-plane to \(P\), and let \(c\) be the distance from the xy-plane to \(P\). We represent the point \(P\) by the ordered triple \((a, b, c)\) of real numbers and we call \(a, b,\) and \(c\) the coordinates of \(P\); \(a\) is the x-coordinate, \(b\) is the y-coordinate, and \(c\) is the z-coordinate. Thus, to locate the point \((a, b, c)\), we can start at the origin \(O\) and move \(a\) units along the x-axis, then \(b\) units parallel to the y-axis, and then \(c\) units parallel to the z-axis as in Figure 4.
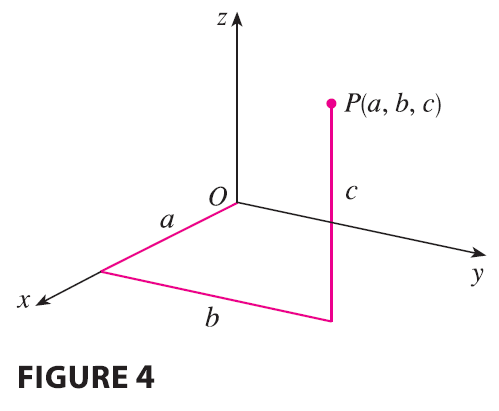
The point \(P(a, b, c)\) determines a rectangular box as in Figure 5. If we drop a perpendicular from \(P\) to the xy-plane, we get a point \(Q\) with coordinates \((a, b, 0)\) called the projection of \(P\) onto the xy-plane. Similarly, \(R(0, b, c)\) and \(S(a, 0, c)\) are the projections of \(P\) onto the yz-plane and xz-plane, respectively.
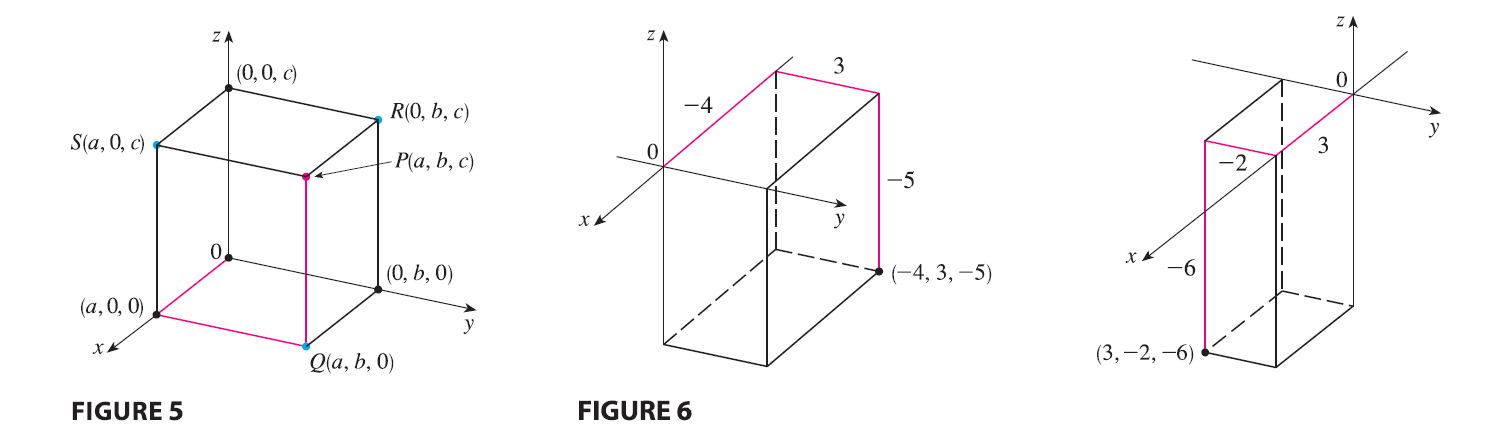
As numerical illustrations, the points \((-4, 3, -5)\) and \((3, -2, -6)\) are plotted in Figure 6.
The Cartesian product \(\mathbb{R} \times \mathbb{R} \times \mathbb{R} = \{(x, y, z) | x, y, z \in \mathbb{R}\}\) is the set of all ordered triples of real numbers and is denoted by \(\mathbb{R}^3\). We have given a one-to-one correspondence between points \(P\) in space and ordered triples \((a, b, c)\) in \(\mathbb{R}^3\). It is called a three-dimensional rectangular coordinate system. Notice that, in terms of coordinates, the first octant can be described as the set of points whose coordinates are all positive.
Surfaces
In two-dimensional analytic geometry, the graph of an equation involving \(x\) and \(y\) is a curve in \(\mathbb{R}^2\). In three-dimensional analytic geometry, an equation in \(x, y,\) and \(z\) represents a surface in \(\mathbb{R}^3\).
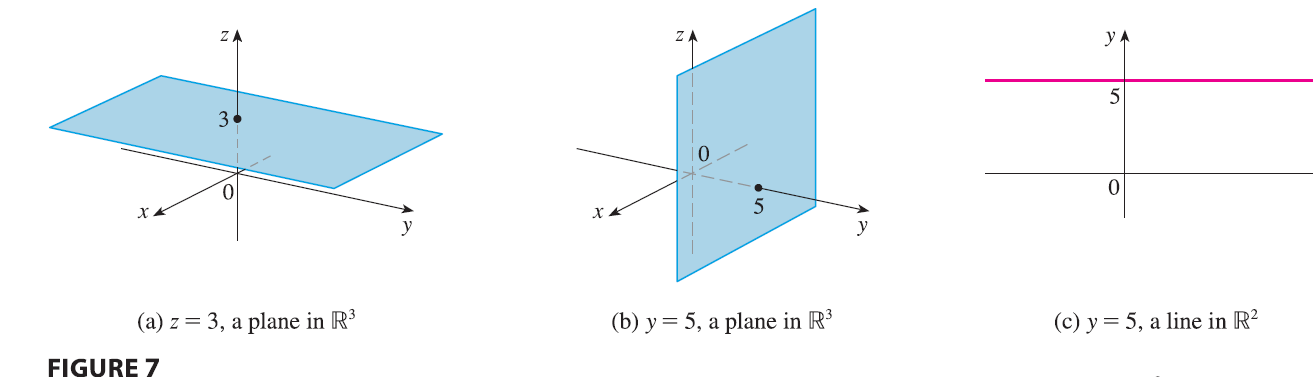
EXAMPLE 1 What surfaces in \(\mathbb{R}^3\) are represented by the following equations? (a) \(z = 3\) (b) \(y = 5\)
In general, if \(k\) is a constant, then \(x = k\) represents a plane parallel to the yz-plane, \(y = k\) is a plane parallel to the xz-plane, and \(z = k\) is a plane parallel to the xy-plane. In Figure 5, the faces of the rectangular box are formed by the three coordinate planes \(x = 0\) (the yz-plane), \(y = 0\) (the xz-plane), and \(z = 0\) (the xy-plane), and the planes \(x = a, y = b,\) and \(z = c\).
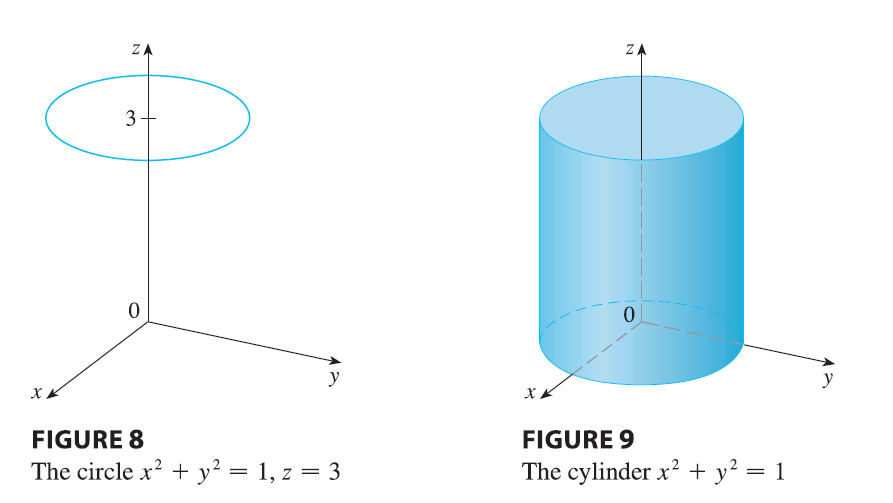
EXAMPLE 2 (a) Which points \((x, y, z)\) satisfy the equations \(x^2 + y^2 = 1\) and \(z = 3\)? (b) What does the equation \(x^2 + y^2 = 1\) represent as a surface in \(\mathbb{R}^3\)?
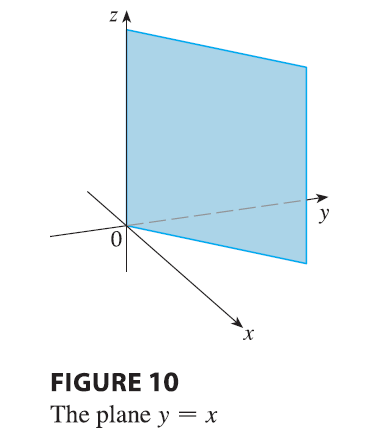
EXAMPLE 3 Describe and sketch the surface in \(\mathbb{R}^3\) represented by the equation \(y = x\).
Distance and Spheres
The familiar formula for the distance between two points in a plane is easily extended to the following three-dimensional formula.
Distance Formula in Three Dimensions The distance \(|P_1P_2|\) between the points \(P_1(x_1, y_1, z_1)\) and \(P_2(x_2, y_2, z_2)\) is \[ |P_1P_2| = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \]
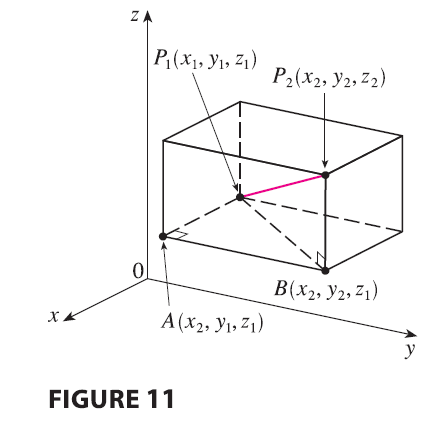
To see why this formula is true, we construct a rectangular box as in Figure 11, where \(P_1\) and \(P_2\) are opposite vertices and the faces of the box are parallel to the coordinate planes. If \(A(x_2, y_1, z_1)\) and \(B(x_2, y_2, z_1)\) are the vertices of the box indicated in the figure, then \[ |P_1A| = |x_2 - x_1| \quad |AB| = |y_2 - y_1| \quad |BP_2| = |z_2 - z_1| \] Because triangles \(P_1BP_2\) and \(P_1AB\) are both right-angled, two applications of the Pythagorean Theorem give \[ |P_1P_2|^2 = |P_1B|^2 + |BP_2|^2 \] and \[ |P_1B|^2 = |P_1A|^2 + |AB|^2 \] Combining these equations, we get \[ |P_1P_2|^2 = |P_1A|^2 + |AB|^2 + |BP_2|^2 = |x_2 - x_1|^2 + |y_2 - y_1|^2 + |z_2 - z_1|^2 \] \[ = (x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 \] Therefore \[ |P_1P_2| = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \]
EXAMPLE 4 The distance from the point \(P(2, -1, 7)\) to the point \(Q(1, -3, 5)\) is \[ |PQ| = \sqrt{(1 - 2)^2 + (-3 - (-1))^2 + (5 - 7)^2} = \sqrt{1 + 4 + 4} = 3 \]
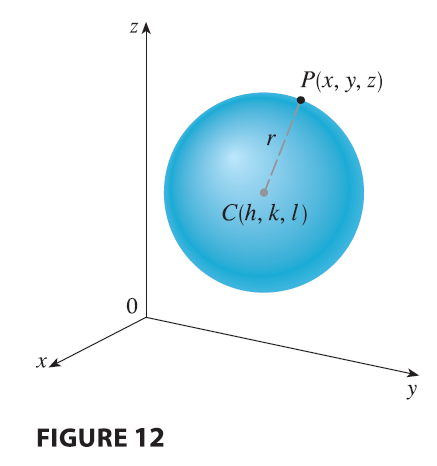
EXAMPLE 5 Find an equation of a sphere with radius \(r\) and center \(C(h, k, l)\).
Equation of a Sphere An equation of a sphere with center \(C(h, k, l)\) and radius \(r\) is \[ (x - h)^2 + (y - k)^2 + (z - l)^2 = r^2 \] In particular, if the center is the origin \(O\), then an equation of the sphere is \[ x^2 + y^2 + z^2 = r^2 \]
EXAMPLE 6 Show that \(x^2 + y^2 + z^2 + 4x - 6y + 2z + 6 = 0\) is the equation of a sphere, and find its center and radius.
EXAMPLE 7 What region in \(\mathbb{R}^3\) is represented by the following inequalities? \[ 1 \le x^2 + y^2 + z^2 \le 4 \quad z \le 0 \]
Exercise 1
Suppose you start at the origin, move along the x-axis a distance of 4 units in the positive direction, and then move downward a distance of 3 units. What are the coordinates of your position?
Exercise 2
Sketch the points (1, 5, 3), (0, 2, -3), (-3, 0, 2), and (2, -2, -1) on a single set of coordinate axes.
Exercise 3
Which of the points A(-4, 0, -1), B(3, 1, -5), and C(2, 4, 6) is closest to the yz-plane? Which point lies in the xz-plane?
Exercise 4
What are the projections of the point (2, 3, 5) on the xy-, yz-, and xz-planes? Draw a rectangular box with the origin and (2, 3, 5) as opposite vertices and with its faces parallel to the coordinate planes. Label all vertices of the box. Find the length of the diagonal of the box.
Exercise 5
What does the equation \(x = 4\) represent in \(\mathbb{R}^2\)? What does it represent in \(\mathbb{R}^3\)? Illustrate with sketches.
Exercise 6
What does the equation \(y = 3\) represent in \(\mathbb{R}^3\)? What does \(z = 5\) represent? What does the pair of equations \(y = 3, z = 5\) represent? In other words, describe the set of points \((x, y, z)\) such that \(y = 3\) and \(z = 5\). Illustrate with a sketch.
Exercise 7
Describe and sketch the surface in \(\mathbb{R}^3\) represented by the equation \(x + y = 2\).
Exercise 8
Describe and sketch the surface in \(\mathbb{R}^3\) represented by the equation \(x^2 + z^2 = 9\).
Exercise 9
Find the lengths of the sides of the triangle PQR. Is it a right triangle? Is it an isosceles triangle? \(P(3, -2, -3), Q(7, 0, 1), R(1, 2, 1)\)
Exercise 10
Find the lengths of the sides of the triangle PQR. Is it a right triangle? Is it an isosceles triangle? \(P(2, -1, 0), Q(4, 1, 1), R(4, -5, 4)\)
Exercise 11
Determine whether the points lie on a straight line. (a) \(A(2, 4, 2), B(3, 7, -2), C(1, 3, 3)\) (b) \(D(0, -5, 5), E(1, -2, 4), F(3, 4, 2)\)
Exercise 12
Find the distance from (4, -2, 6) to each of the following. (a) The xy-plane (b) The yz-plane (c) The xz-plane (d) The x-axis (e) The y-axis (f) The z-axis
Exercise 13
Find an equation of the sphere with center (-3, 2, 5) and radius 4. What is the intersection of this sphere with the yz-plane?
Exercise 14
Find an equation of the sphere with center (2, -6, 4) and radius 5. Describe its intersection with each of the coordinate planes.
Exercise 15
Find an equation of the sphere that passes through the point (4, 3, -1) and has center (3, 8, 1).
Exercise 16
Find an equation of the sphere that passes through the origin and whose center is (1, 2, 3).
Exercise 17
Show that the equation \(x^2 + y^2 + z^2 - 2x - 4y + 8z = 15\) represents a sphere, and find its center and radius.
Exercise 18
Show that the equation \(x^2 + y^2 + z^2 + 8x - 6y + 2z + 17 = 0\) represents a sphere, and find its center and radius.
Exercise 19
Show that the equation \(2x^2 + 2y^2 + 2z^2 = 8x - 24z + 1\) represents a sphere, and find its center and radius.
Exercise 20
Show that the equation \(3x^2 + 3y^2 + 3z^2 = 10 + 6y + 12z\) represents a sphere, and find its center and radius.
Exercise 21
- Prove that the midpoint of the line segment from \(P_1(x_1, y_1, z_1)\) to \(P_2(x_2, y_2, z_2)\) is \[ \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2} \right) \]
- Find the lengths of the medians of the triangle with vertices A(1, 2, 3), B(-2, 0, 5), and C(4, 1, 5). (A median of a triangle is a line segment that joins a vertex to the midpoint of the opposite side.)
Exercise 22
Find an equation of a sphere if one of its diameters has endpoints (5, 4, 3) and (1, 6, -9).
Exercise 23
Find equations of the spheres with center (2, -3, 6) that touch (a) the xy-plane, (b) the yz-plane, (c) the xz-plane.
Exercise 24
Find an equation of the largest sphere with center (5, 4, 9) that is contained in the first octant.
Exercise 25
Describe in words the region of \(\mathbb{R}^3\) represented by the equation \(x = 5\).
Exercise 26
Describe in words the region of \(\mathbb{R}^3\) represented by the equation \(y = -2\).
Exercise 27
Describe in words the region of \(\mathbb{R}^3\) represented by the inequality \(y < 8\).
Exercise 28
Describe in words the region of \(\mathbb{R}^3\) represented by the inequality \(z \ge -1\).
Exercise 29
Describe in words the region of \(\mathbb{R}^3\) represented by the inequality \(0 \le z \le 6\).
Exercise 30
Describe in words the region of \(\mathbb{R}^3\) represented by the equation \(y^2 = 4\).
Exercise 31
Describe in words the region of \(\mathbb{R}^3\) represented by the equations \(x^2 + y^2 = 4, z = -1\).
Exercise 32
Describe in words the region of \(\mathbb{R}^3\) represented by the equation \(x^2 + y^2 = 4\).
Exercise 33
Describe in words the region of \(\mathbb{R}^3\) represented by the equation \(x^2 + y^2 + z^2 = 4\).
Exercise 34
Describe in words the region of \(\mathbb{R}^3\) represented by the inequality \(x^2 + y^2 + z^2 \le 4\).
Exercise 35
Describe in words the region of \(\mathbb{R}^3\) represented by the inequality \(1 \le x^2 + y^2 + z^2 \le 5\).
Exercise 36
Describe in words the region of \(\mathbb{R}^3\) represented by the equation \(x = z\).
Exercise 37
Describe in words the region of \(\mathbb{R}^3\) represented by the inequality \(x^2 + z^2 \le 9\).
Exercise 38
Describe in words the region of \(\mathbb{R}^3\) represented by the inequality \(x^2 + y^2 + z^2 > 2z\).
Exercise 39
Write inequalities to describe the region: The region between the yz-plane and the vertical plane \(x = 5\).
Exercise 40
Write inequalities to describe the region: The solid cylinder that lies on or below the plane \(z = 8\) and on or above the disk in the xy-plane with center the origin and radius 2.
Exercise 41
Write inequalities to describe the region: The region consisting of all points between (but not on) the spheres of radius \(r\) and \(R\) centered at the origin, where \(r < R\).
Exercise 42
Write inequalities to describe the region: The solid upper hemisphere of the sphere of radius 2 centered at the origin.
Exercise 43
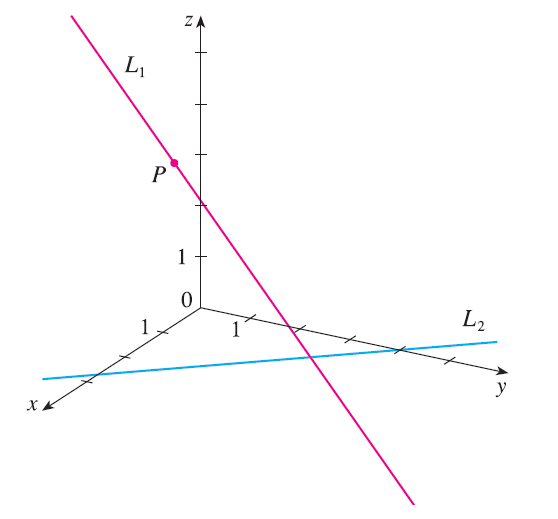
The figure shows a line \(L_1\) in space and a second line \(L_2\), which is the projection of \(L_1\) onto the xy-plane. (In other words, the points on \(L_2\) are directly beneath, or above, the points on \(L_1\).) (a) Find the coordinates of the point P on the line \(L_1\). (b) Locate on the diagram the points A, B, and C, where the line \(L_1\) intersects the xy-plane, the yz-plane, and the xz-plane, respectively.
Exercise 44
Consider the points P such that the distance from P to A(-1, 5, 3) is twice the distance from P to B(6, 2, -2). Show that the set of all such points is a sphere, and find its center and radius.
Exercise 45
Find an equation of the set of all points equidistant from the points A(-1, 5, 3) and B(6, 2, -2). Describe the set.
Exercise 46
Find the volume of the solid that lies inside both of the spheres \(x^2 + y^2 + z^2 + 4x - 2y + 4z + 5 = 0\) and \(x^2 + y^2 + z^2 = 4\)
Exercise 47
Find the distance between the spheres \(x^2 + y^2 + z^2 = 4\) and \(x^2 + y^2 + z^2 = 4x + 4y + 4z - 11\).
Exercise 48
Describe and sketch a solid with the following properties. When illuminated by rays parallel to the z-axis, its shadow is a circular disk. If the rays are parallel to the y-axis, its shadow is a square. If the rays are parallel to the x-axis, its shadow is an isosceles triangle.