Section 12.2: Vectors
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 12.2: Vectors |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 4:07 AM |
Table of contents
- Vectors
- Combining Vectors - Vector Addition
- Scalar Multiplication of vectors
- Difference of two vectors
- Components of vector
- Magnitude or Length of vectors
- How do we add vectors algebraically?
- N-dimensional vectors
- Properties of Vectors
- Standard basis vectors
- Unit Vector
- Applications of vectors
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
- Exercise 49
- Exercise 50
- Exercise 51
- Exercise 52
Vectors
The term vector is used by scientists to indicate a quantity (such as displacement or velocity or force) that has both magnitude and direction.
A vector is often represented by an arrow or a directed line segment. The length of the arrow represents the magnitude of the vector and the arrow points in the direction of the vector. We denote a vector by printing a letter in boldface (v) or by putting an arrow above the letter (\(\vec{v}\)).
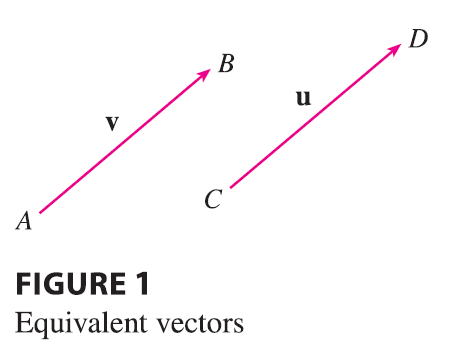
For instance, suppose a particle moves along a line segment from point A to point B. The corresponding displacement vector v, shown in Figure 1, has initial point A (the tail) and terminal point B (the tip) and we indicate this by writing \(\mathbf{v} = \vec{AB}\). Notice that the vector \(\mathbf{u} = \vec{CD}\) has the same length and the same direction as v even though it is in a different position. We say that u and v are equivalent (or equal) and we write \(\mathbf{u} = \mathbf{v}\). The zero vector, denoted by 0, has length 0. It is the only vector with no specific direction.
Combining Vectors - Vector Addition
Suppose a particle moves from A to B, so its displacement vector is \(\vec{AB}\). Then the particle changes direction and moves from B to C, with displacement vector \(\vec{BC}\) as in Figure 2.
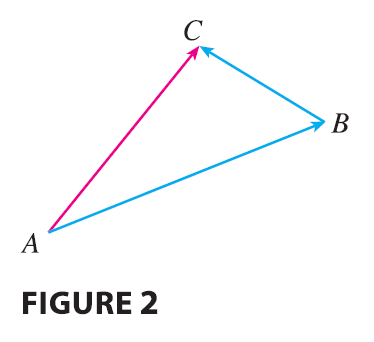
The combined effect of these displacements is that the particle has moved from A to C. The resulting displacement vector \(\vec{AC}\) is called the sum of \(\vec{AB}\) and \(\vec{BC}\) and we write \[ \vec{AC} = \vec{AB} + \vec{BC} \] In general, if we start with vectors u and v, we first move v so that its tail coincides with the tip of u and define the sum of u and v as follows.
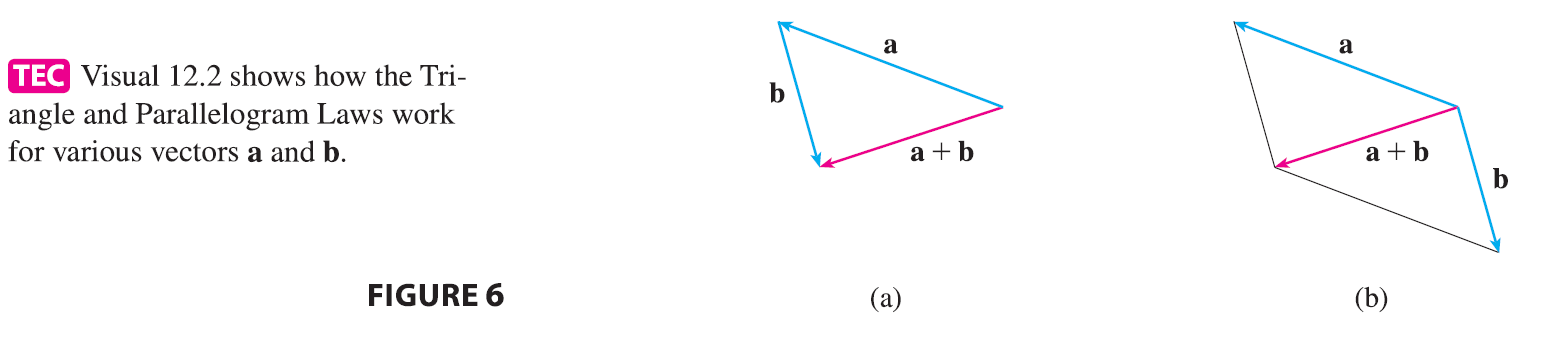
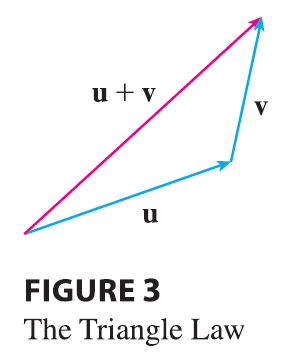
Definition of Vector Addition If u and v are vectors positioned so the initial point of v is at the terminal point of u, then the sum \(\mathbf{u} + \mathbf{v}\) is the vector from the initial point of u to the terminal point of v.
The definition of vector addition is illustrated in Figure 3. You can see why this definition is sometimes called the Triangle Law.
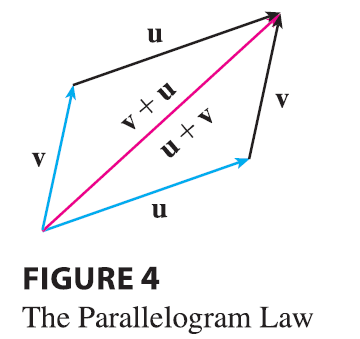
In Figure 4 we start with the same vectors u and v as in Figure 3 and draw another copy of v with the same initial point as u. Completing the parallelogram, we see that \(\mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}\). This also gives another way to construct the sum: if we place u and v so they start at the same point, then \(\mathbf{u} + \mathbf{v}\) lies along the diagonal of the parallelogram with u and v as sides. (This is called the Parallelogram Law.)
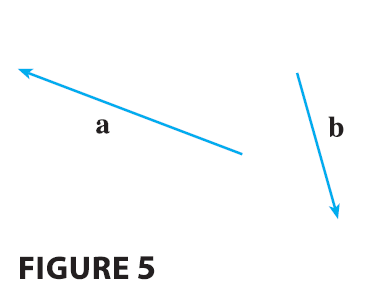
EXAMPLE 1 Draw the sum of the vectors a and b shown in Figure 5.
Scalar Multiplication of vectors
It is possible to multiply a vector by a real number \(c\). (In this context we call the real number \(c\) a scalar to distinguish it from a vector.) For instance, we want \(2\mathbf{v}\) to be the same vector as \(\mathbf{v} + \mathbf{v}\), which has the same direction as v but is twice as long. In general, we multiply a vector by a scalar as follows.
Definition of Scalar Multiplication If \(c\) is a scalar and v is a vector, then the scalar multiple \(c\mathbf{v}\) is the vector whose length is \(|c|\) times the length of v and whose direction is the same as v if \(c > 0\) and is opposite to v if \(c < 0\). If \(c = 0\) or \(\mathbf{v} = \mathbf{0}\), then \(c\mathbf{v} = \mathbf{0}\).
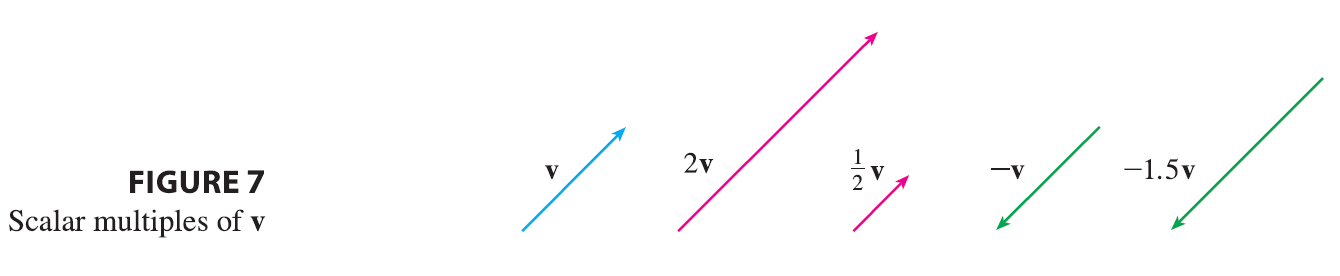
This definition is illustrated in Figure 7. We see that real numbers work like scaling factors here; that’s why we call them scalars. Notice that two nonzero vectors are parallel if they are scalar multiples of one another. In particular, the vector \(-\mathbf{v} = (-1)\mathbf{v}\) has the same length as v but points in the opposite direction. We call it the negative of v.
Difference of two vectors
Recall, the vector \(-\mathbf{v} = (-1)\mathbf{v}\) has the same length as v but points in the opposite direction. We call it the negative of v.
By the difference \(\mathbf{u} - \mathbf{v}\) of two vectors we mean \[ \mathbf{u} - \mathbf{v} = \mathbf{u} + (-\mathbf{v}) \]
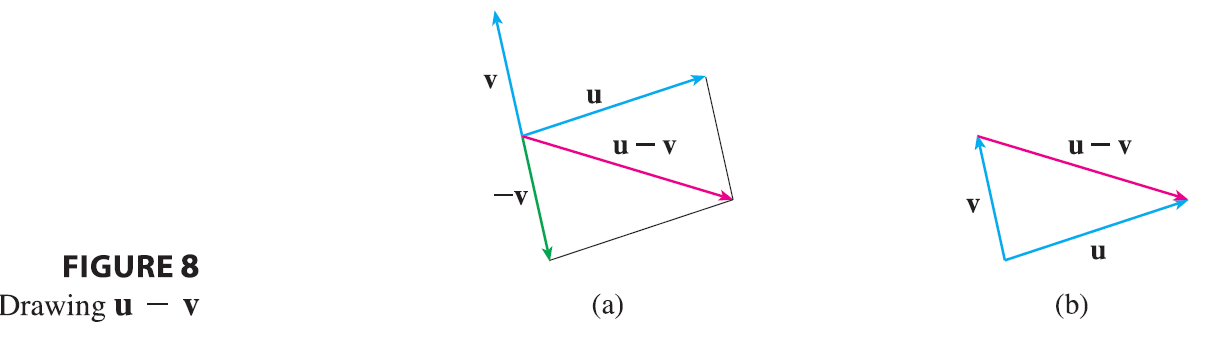
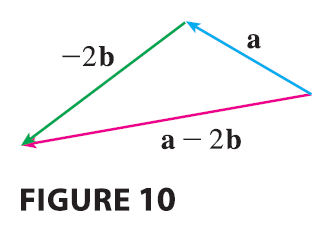
So we can construct \(\mathbf{u} - \mathbf{v}\) by first drawing the negative of v, \(-\mathbf{v}\), and then adding it to u by the Parallelogram Law as in Figure 8(a). Alternatively, since \(\mathbf{v} + (\mathbf{u} - \mathbf{v}) = \mathbf{u}\), the vector \(\mathbf{u} - \mathbf{v}\), when added to v, gives u. So we could construct \(\mathbf{u} - \mathbf{v}\) as in Figure 8(b) by means of the Triangle Law. Notice that if u and v both start from the same initial point, then \(\mathbf{u} - \mathbf{v}\) connects the tip of v to the tip of u.
EXAMPLE 2 If a and
b are the vectors shown in Figure 9, draw \(\mathbf{a} - 2\mathbf{b}\). 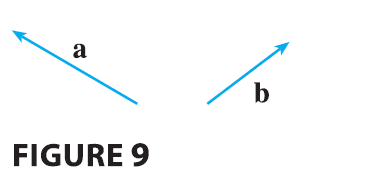
Components of vector
For some purposes it’s best to introduce a coordinate system and treat vectors algebraically. If we place the initial point of a vector a at the origin of a rectangular coordinate system, then the terminal point of a has coordinates of the form \((a_1, a_2)\) or \((a_1, a_2, a_3)\), depending on whether our coordinate system is two- or three-dimensional (see Figure 11).
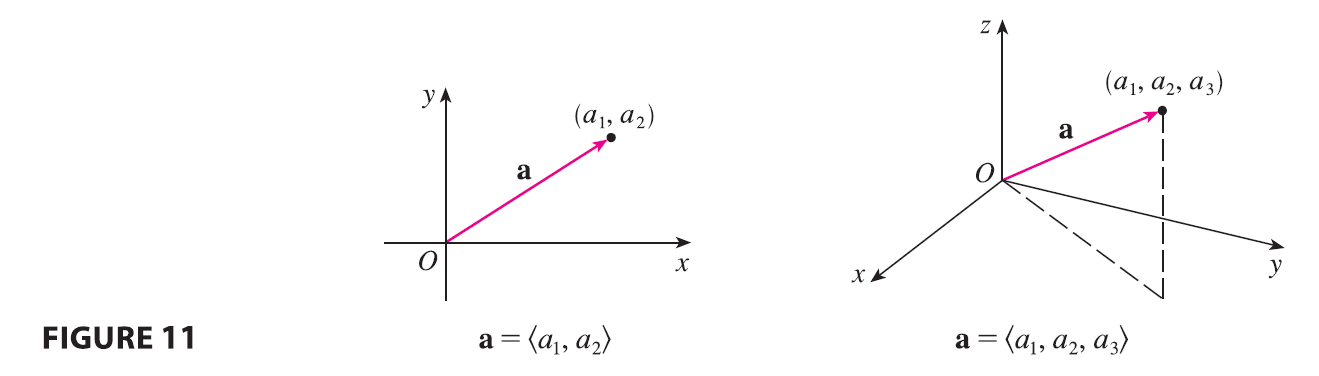
These coordinates are called the components of a and we write \[ \mathbf{a} = \langle a_1, a_2 \rangle \quad \text{or} \quad \mathbf{a} = \langle a_1, a_2, a_3 \rangle \]
We use the notation \(\langle a_1, a_2 \rangle\) for the ordered pair that refers to a vector so as not to confuse it with the ordered pair \((a_1, a_2)\) that refers to a point in the plane.
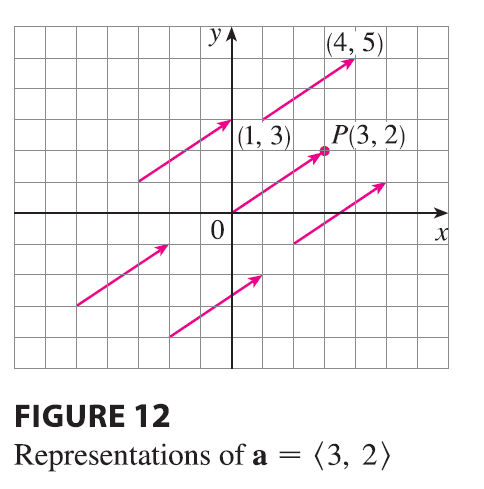
For instance, the vectors shown in Figure 12 are all equivalent to the vector \(\vec{OP} = \langle 3, 2 \rangle\) whose terminal point is \(P(3, 2)\). What they have in common is that the terminal point is reached from the initial point by a displacement of three units to the right and two upward. We can think of all these geometric vectors as representations of the algebraic vector \(\mathbf{a} = \langle 3, 2 \rangle\). The particular representation \(\vec{OP}\) from the origin to the point \(P(3, 2)\) is called the position vector of the point \(P\).
In three dimensions, the vector \(\mathbf{a} = \vec{OP} = \langle a_1, a_2, a_3 \rangle\) is the position vector of the point \(P(a_1, a_2, a_3)\). (See Figure 13.)
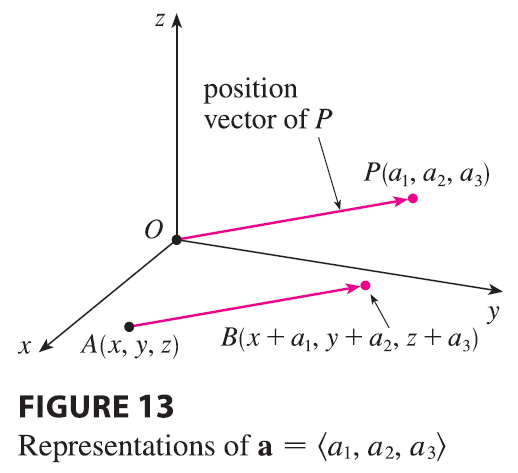
Let’s consider any other representation \(\vec{AB}\) of a, where the initial point is \(A(x_1, y_1, z_1)\) and the terminal point is \(B(x_2, y_2, z_2)\). Then we must have \(x_1 + a_1 = x_2, y_1 + a_2 = y_2,\) and \(z_1 + a_3 = z_2\) and so \(a_1 = x_2 - x_1, a_2 = y_2 - y_1,\) and \(a_3 = z_2 - z_1\). Thus we have the following result.
Given the points \(A(x_1, y_1, z_1)\) and \(B(x_2, y_2, z_2)\), the vector a with representation \(\vec{AB}\) is \[ \mathbf{a} = \langle x_2 - x_1, y_2 - y_1, z_2 - z_1 \rangle \tag{1} \]
EXAMPLE 3 Find the vector represented by the directed line segment with initial point \(A(2, -3, 4)\) and terminal point \(B(-2, 1, 1)\).
Magnitude or Length of vectors
The magnitude or length of the vector v is the length of any of its representations and is denoted by the symbol \(|\mathbf{v}|\) or \(||\mathbf{v}||\). By using the distance formula to compute the length of a segment OP, we obtain the following formulas.
The length of the two-dimensional vector \(\mathbf{a} = \langle a_1, a_2 \rangle\) is \[ |\mathbf{a}| = \sqrt{a_1^2 + a_2^2} \] The length of the three-dimensional vector \(\mathbf{a} = \langle a_1, a_2, a_3 \rangle\) is \[ |\mathbf{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2} \]
How do we add vectors algebraically?
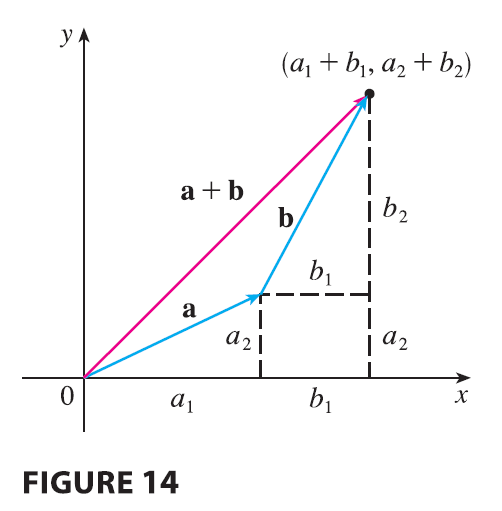
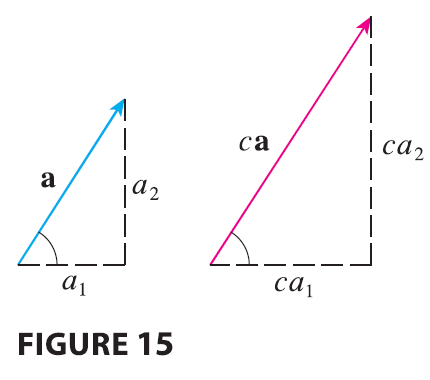
Figure 14 shows that if \(\mathbf{a} = \langle a_1, a_2 \rangle\) and \(\mathbf{b} = \langle b_1, b_2 \rangle\), then the sum is \(\mathbf{a} + \mathbf{b} = \langle a_1 + b_1, a_2 + b_2 \rangle\), at least for the case where the components are positive. In other words, to add algebraic vectors we add corresponding components. Similarly, to subtract vectors we subtract corresponding components. From the similar triangles in Figure 15 we see that the components of \(c\mathbf{a}\) are \(ca_1\) and \(ca_2\). So to multiply a vector by a scalar we multiply each component by that scalar.
If \(\mathbf{a} = \langle a_1, a_2 \rangle\) and \(\mathbf{b} = \langle b_1, b_2 \rangle\), then \[ \mathbf{a} + \mathbf{b} = \langle a_1 + b_1, a_2 + b_2 \rangle \quad \mathbf{a} - \mathbf{b} = \langle a_1 - b_1, a_2 - b_2 \rangle \] \[ c\mathbf{a} = \langle ca_1, ca_2 \rangle \] Similarly, for three-dimensional vectors, \[ \langle a_1, a_2, a_3 \rangle + \langle b_1, b_2, b_3 \rangle = \langle a_1 + b_1, a_2 + b_2, a_3 + b_3 \rangle \] \[ \langle a_1, a_2, a_3\rangle - \langle b_1, b_2, b_3 \rangle = \langle a_1 - b_1, a_2 - b_2, a_3 - b_3 \rangle \] \[ c\langle a_1, a_2, a_3 \rangle = \langle ca_1, ca_2, ca_3 \rangle \]
EXAMPLE 4 If \(\mathbf{a} = \langle 4, 0, 3 \rangle\) and \(\mathbf{b} = \langle -2, 1, 5 \rangle\), find \(|\mathbf{a}|\) and the vectors \(\mathbf{a} + \mathbf{b}, \mathbf{a} - \mathbf{b}, 3\mathbf{b},\) and \(2\mathbf{a} + 5\mathbf{b}\).
N-dimensional vectors
We denote by \(V_2\) the set of all two-dimensional vectors and by \(V_3\) the set of all three-dimensional vectors. More generally, we will later need to consider the set \(V_n\) of all n-dimensional vectors. An n-dimensional vector is an ordered n-tuple: \[ \mathbf{a} = \langle a_1, a_2, ..., a_n \rangle \] where \(a_1, a_2, ..., a_n\) are real numbers that are called the components of a. Addition and scalar multiplication are defined in terms of components just as for the cases \(n = 2\) and \(n = 3\).
Properties of Vectors
Properties of Vectors If a, b, and c are vectors in \(V_n\) and \(c\) and \(d\) are scalars, then 1. \(\mathbf{a} + \mathbf{b} = \mathbf{b} + \mathbf{a}\) 2. \(\mathbf{a} + (\mathbf{b} + \mathbf{c}) = (\mathbf{a} + \mathbf{b}) + \mathbf{c}\) 3. \(\mathbf{a} + \mathbf{0} = \mathbf{a}\) 4. \(\mathbf{a} + (-\mathbf{a}) = \mathbf{0}\) 5. \(c(\mathbf{a} + \mathbf{b}) = c\mathbf{a} + c\mathbf{b}\) 6. \((c + d)\mathbf{a} = c\mathbf{a} + d\mathbf{a}\) 7. \((cd)\mathbf{a} = c(d\mathbf{a})\) 8. \(1\mathbf{a} = \mathbf{a}\) —
These eight properties of vectors can be readily verified either geometrically or algebraically. For instance, Property 1 can be seen from Figure 4 (it’s equivalent to the Parallelogram Law) or as follows for the case \(n = 2\): \[ \mathbf{a} + \mathbf{b} = \langle a_1, a_2 \rangle + \langle b_1, b_2 \rangle = \langle a_1 + b_1, a_2 + b_2 \rangle \] \[ = \langle b_1 + a_1, b_2 + a_2 \rangle = \langle b_1, b_2 \rangle + \langle a_1, a_2 \rangle = \mathbf{b} + \mathbf{a} \] We can see why Property 2 (the associative law) is true by looking at Figure 16 and applying the Triangle Law several times: the vector \(\vec{PQ}\) is obtained either by first constructing \(\mathbf{a} + \mathbf{b}\) and then adding c or by adding a to the vector \(\mathbf{b} + \mathbf{c}\).
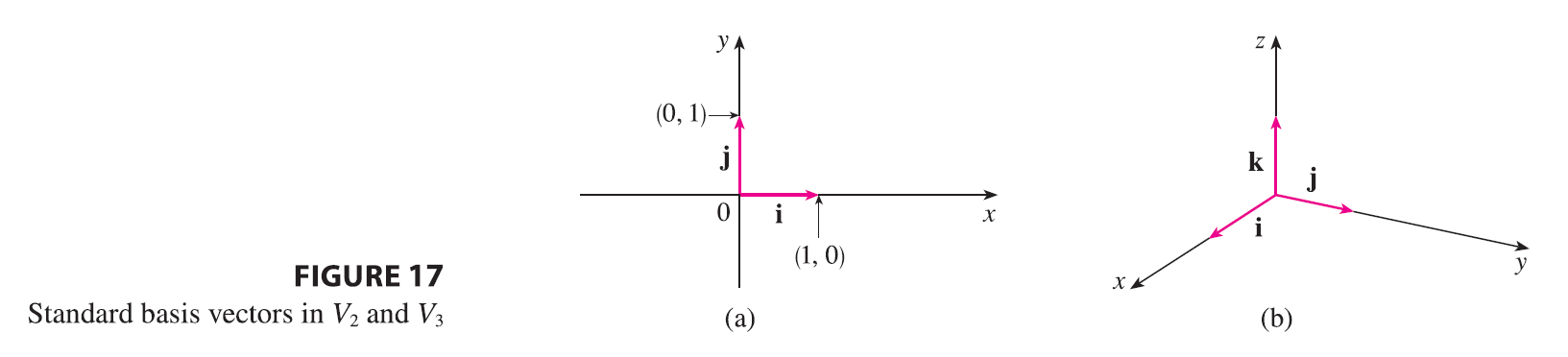
Standard basis vectors
Three vectors in \(V_3\) play a special role. Let \[ \mathbf{i} = \langle 1, 0, 0 \rangle \quad \mathbf{j} = \langle 0, 1, 0 \rangle \quad \mathbf{k} = \langle 0, 0, 1 \rangle \]
These vectors i, j, and k are called the standard basis vectors. They have length 1 and point in the directions of the positive x-, y-, and z-axes. Similarly, in two dimensions we define \(\mathbf{i} = \langle 1, 0 \rangle\) and \(\mathbf{j} = \langle 0, 1 \rangle\). (See Figure 17.)
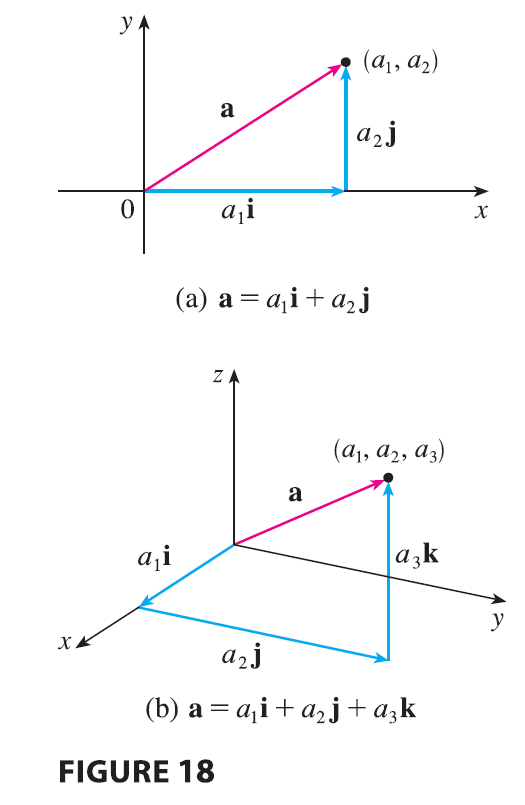
| If \(\mathbf{a} = \langle a_1, a_2, a_3 \rangle\), then we can write \[ \mathbf{a} = \langle a_1, a_2, a_3 \rangle = \langle a_1, 0, 0 \rangle + \langle 0, a_2, 0 \rangle + \langle 0, 0, a_3 \rangle \] \[ = a_1\langle 1, 0, 0 \rangle + a_2\langle 0, 1, 0 \rangle + a_3\langle 0, 0, 1 \rangle \] \[ \mathbf{a} = a_1\mathbf{i} + a_2\mathbf{j} + a_3\mathbf{k} \tag{2} \] Thus any vector in \(V_3\) can be expressed in terms of i, j, and k. For instance, \[ \langle 1, -2, 6 \rangle = \mathbf{i} - 2\mathbf{j} + 6\mathbf{k} \] Similarly, in two dimensions, we can write \[ \mathbf{a} = \langle a_1, a_2 \rangle = a_1\mathbf{i} + a_2\mathbf{j} \tag{3} \] See Figure 18 for the geometric interpretation of Equations 3 and 2 and compare with Figure 17. |
 |
EXAMPLE 5 If \(\mathbf{a} = \mathbf{i} + 2\mathbf{j} - 3\mathbf{k}\) and \(\mathbf{b} = 4\mathbf{i} + 7\mathbf{k}\), express the vector \(2\mathbf{a} + 3\mathbf{b}\) in terms of i, j, and k.
Unit Vector
A unit vector is a vector whose length is 1. For instance, i, j, and k are all unit vectors. In general, if \(\mathbf{a} \ne \mathbf{0}\), then the unit vector that has the same direction as a is \[ \mathbf{u} = \frac{1}{|\mathbf{a}|}\mathbf{a} = \frac{\mathbf{a}}{|\mathbf{a}|} \tag{4} \] In order to verify this, we let \(c = 1/|\mathbf{a}|\). Then \(\mathbf{u} = c\mathbf{a}\) and \(c\) is a positive scalar, so u has the same direction as a. Also \[ |\mathbf{u}| = |c\mathbf{a}| = |c||\mathbf{a}| = \frac{1}{|\mathbf{a}|}|\mathbf{a}| = 1 \]
EXAMPLE 6 Find the unit vector in the direction of the vector \(2\mathbf{i} - \mathbf{j} - 2\mathbf{k}\).
Applications of vectors
Vectors are useful in many aspects of physics and engineering. In Chapter 13 we will see how they describe the velocity and acceleration of objects moving in space. Here we look at forces.
A force is represented by a vector because it has both a magnitude (measured in pounds or newtons) and a direction. If several forces are acting on an object, the resultant force experienced by the object is the vector sum of these forces.
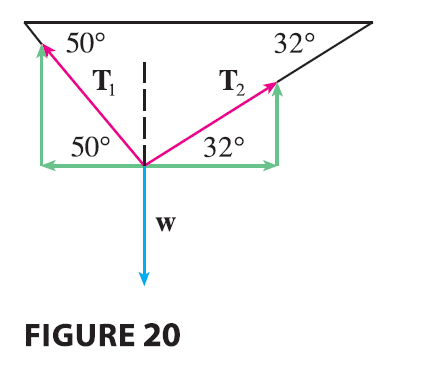
EXAMPLE 7 A 100-lb weight hangs from two wires as shown in Figure 19. Find the tensions (forces) \(\mathbf{T}_1\) and \(\mathbf{T}_2\) in both wires and the magnitudes of the tensions.
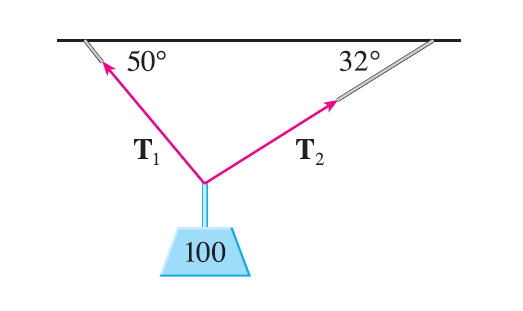
Exercise 1
Are the following quantities vectors or scalars? Explain. (a) The cost of a theater ticket (b) The current in a river (c) The initial flight path from Houston to Dallas (d) The population of the world
Exercise 2
What is the relationship between the point (4, 7) and the vector \(\langle 4, 7 \rangle\)? Illustrate with a sketch.
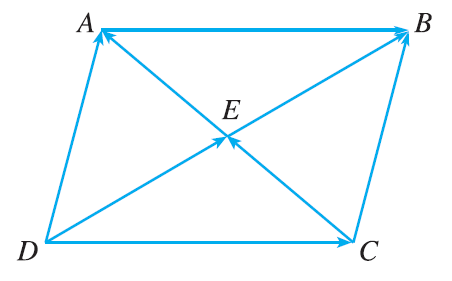
Exercise 3
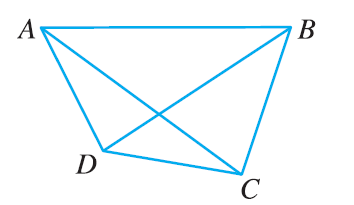
Name all the equal vectors in the parallelogram shown.
Exercise 4
Write each combination of vectors as a single vector. (a) \(\vec{AB} + \vec{BC}\) (b) \(\vec{CD} + \vec{DB}\) (c) \(\vec{DB} - \vec{AB}\) (d) \(\vec{DC} + \vec{CA} + \vec{AB}\)
Exercise 5
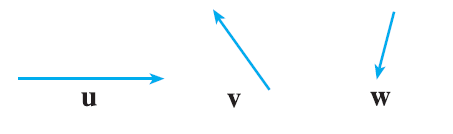
Copy the vectors in the figure and use them to draw the following vectors. (a) \(\mathbf{u} + \mathbf{v}\) (b) \(\mathbf{u} + \mathbf{w}\) (c) \(\mathbf{v} + \mathbf{w}\) (d) \(\mathbf{u} - \mathbf{v}\) (e) \(\mathbf{v} + \mathbf{u} + \mathbf{w}\) (f) \(\mathbf{u} - \mathbf{w} - \mathbf{v}\)
Exercise 6
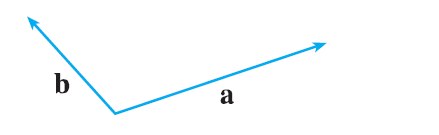
Copy the vectors in the figure and use them to draw the following vectors. (a) \(\mathbf{a} + \mathbf{b}\) (b) \(\mathbf{a} - \mathbf{b}\) (c) \(\frac{1}{2}\mathbf{a}\) (d) \(-3\mathbf{b}\) (e) \(\mathbf{a} + 2\mathbf{b}\) (f) \(2\mathbf{b} - \mathbf{a}\)
Exercise 7
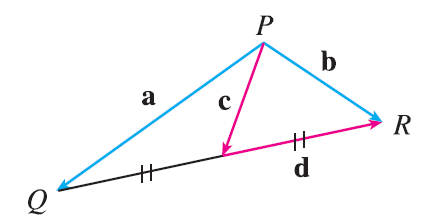
In the figure, the tip of c and the tail of d are both the midpoint of QR. Express c and d in terms of a and b.
Exercise 8
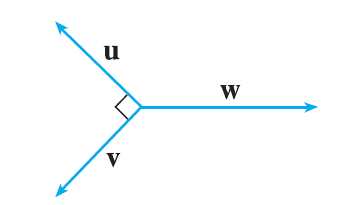
If the vectors in the figure satisfy \(|\mathbf{u}| = |\mathbf{v}| = 1\) and \(\mathbf{u} + \mathbf{v} + \mathbf{w} = \mathbf{0}\), what is \(|\mathbf{w}|\)?
Exercise 9
Find a vector a with representation given by the directed line segment \(\vec{AB}\). Draw \(\vec{AB}\) and the equivalent representation starting at the origin. \(A(-2, 1), B(1, 2)\)
Exercise 10
Find a vector a with representation given by the directed line segment \(\vec{AB}\). Draw \(\vec{AB}\) and the equivalent representation starting at the origin. \(A(-5, -1), B(-3, 3)\)
Exercise 11
Find a vector a with representation given by the directed line segment \(\vec{AB}\). Draw \(\vec{AB}\) and the equivalent representation starting at the origin. \(A(3, -1), B(2, 3)\)
Exercise 12
Find a vector a with representation given by the directed line segment \(\vec{AB}\). Draw \(\vec{AB}\) and the equivalent representation starting at the origin. \(A(3, 2), B(1, 0)\)
Exercise 13
Find a vector a with representation given by the directed line segment \(\vec{AB}\). Draw \(\vec{AB}\) and the equivalent representation starting at the origin. \(A(0, 3, 1), B(2, 3, -1)\)
Exercise 14
Find a vector a with representation given by the directed line segment \(\vec{AB}\). Draw \(\vec{AB}\) and the equivalent representation starting at the origin. \(A(0, 6, -1), B(3, 4, 4)\)
Exercise 15
Find the sum of the given vectors and illustrate geometrically. \(\langle -1, 4 \rangle, \langle 6, -2 \rangle\)
Exercise 16
Find the sum of the given vectors and illustrate geometrically. \(\langle 3, -1 \rangle, \langle -1, 5 \rangle\)
Exercise 17
Find the sum of the given vectors and illustrate geometrically. \(\langle 3, 0, 1 \rangle, \langle 0, 8, 0 \rangle\)
Exercise 18
Find the sum of the given vectors and illustrate geometrically. \(\langle 1, 3, -2 \rangle, \langle 0, 0, 6 \rangle\)
Exercise 19
Find \(\mathbf{a} + \mathbf{b}, 4\mathbf{a} + 2\mathbf{b}, |\mathbf{a}|,\) and \(|\mathbf{a} - \mathbf{b}|\). \(\mathbf{a} = \langle -3, 4 \rangle, \mathbf{b} = \langle 9, -1 \rangle\)
Exercise 20
Find \(\mathbf{a} + \mathbf{b}, 4\mathbf{a} + 2\mathbf{b}, |\mathbf{a}|,\) and \(|\mathbf{a} - \mathbf{b}|\). \(\mathbf{a} = 5\mathbf{i} + 3\mathbf{j}, \mathbf{b} = -\mathbf{i} - 2\mathbf{j}\)
Exercise 21
Find \(\mathbf{a} + \mathbf{b}, 4\mathbf{a} + 2\mathbf{b}, |\mathbf{a}|,\) and \(|\mathbf{a} - \mathbf{b}|\). \(\mathbf{a} = 4\mathbf{i} - 3\mathbf{j} + 2\mathbf{k}, \mathbf{b} = 2\mathbf{i} - 4\mathbf{k}\)
Exercise 22
Find \(\mathbf{a} + \mathbf{b}, 4\mathbf{a} + 2\mathbf{b}, |\mathbf{a}|,\) and \(|\mathbf{a} - \mathbf{b}|\). \(\mathbf{a} = \langle 8, 1, -4 \rangle, \mathbf{b} = \langle 5, -2, 1 \rangle\)
Exercise 23
Find a unit vector that has the same direction as the given vector. \(\langle 6, -2 \rangle\)
Exercise 24
Find a unit vector that has the same direction as the given vector. \(-5\mathbf{i} + 3\mathbf{j} - \mathbf{k}\)
Exercise 25
Find a unit vector that has the same direction as the given vector. \(8\mathbf{i} - \mathbf{j} + 4\mathbf{k}\)
Exercise 26
Find the vector that has the same direction as \(\langle 6, 2, -3 \rangle\) but has length 4.
Exercise 27
What is the angle between the given vector and the positive direction of the x-axis? \(\mathbf{i} + \sqrt{3}\mathbf{j}\)
Exercise 28
What is the angle between the given vector and the positive direction of the x-axis? \(8\mathbf{i} + 6\mathbf{j}\)
Exercise 29
If v lies in the first quadrant and makes an angle \(\pi/3\) with the positive x-axis and \(|\mathbf{v}| = 4\), find v in component form.
Exercise 30
If a child pulls a sled through the snow on a level path with a force of 50 N exerted at an angle of \(38^\circ\) above the horizontal, find the horizontal and vertical components of the force.
Exercise 31
A quarterback throws a football with angle of elevation \(40^\circ\) and speed 60 ft/s. Find the horizontal and vertical components of the velocity vector.
Exercise 32
Find the magnitude of the resultant force and the angle it makes with the positive x-axis.
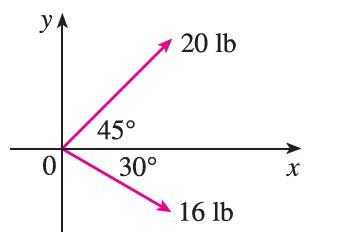
Exercise 33
Find the magnitude of the resultant force and the angle it makes with the positive x-axis.
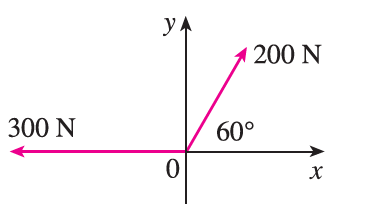
Exercise 34
The magnitude of a velocity vector is called speed. Suppose that a wind is blowing from the direction N45°W at a speed of 50 km/h. (This means that the direction from which the wind blows is 45° west of the northerly direction.) A pilot is steering a plane in the direction N60°E at an airspeed (speed in still air) of 250 km/h. The true course, or track, of the plane is the direction of the resultant of the velocity vectors of the plane and the wind. The ground speed of the plane is the magnitude of the resultant. Find the true course and the ground speed of the plane.
Exercise 35
A woman walks due west on the deck of a ship at 3 mi/h. The ship is moving north at a speed of 22 mi/h. Find the speed and direction of the woman relative to the surface of the water.
Exercise 36
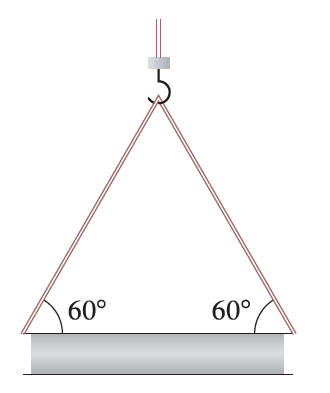
A crane suspends a 500-lb steel beam horizontally by support cables (with negligible weight) attached from a hook to each end of the beam. The support cables each make an angle of \(60^\circ\) with the beam. Find the tension vector in each support cable and the magnitude of each tension.
Exercise 37
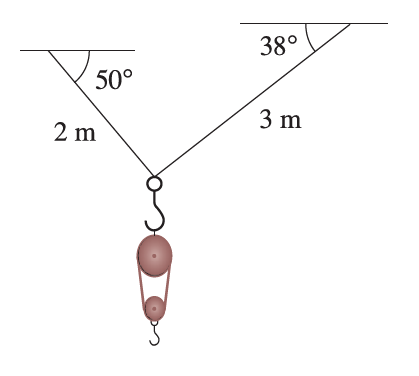
A block-and-tackle pulley hoist is suspended in a warehouse by ropes of lengths 2 m and 3 m. The hoist weighs 350 N. The ropes, fastened at different heights, make angles of \(50^\circ\) and \(38^\circ\) with the horizontal. Find the tension in each rope and the magnitude of each tension.
Exercise 38

The tension T at each end of a chain has magnitude 25 N (see the figure). What is the weight of the chain?
Exercise 39
A boatman wants to cross a canal that is 3 km wide and wants to land at a point 2 km upstream from his starting point. The current in the canal flows at 3.5 km/h and the speed of his boat is 13 km/h. (a) In what direction should he steer? (b) How long will the trip take?
Exercise 40
Three forces act on an object. Two of the forces are at an angle of \(100^\circ\) to each other and have magnitudes 25 N and 12 N. The third is perpendicular to the plane of these two forces and has magnitude 4 N. Calculate the magnitude of the force that would exactly counterbalance these three forces.
Exercise 41
Find the unit vectors that are parallel to the tangent line to the parabola \(y = x^2\) at the point (2, 4).
Exercise 42
- Find the unit vectors that are parallel to the tangent line to the curve \(y = 2 \sin x\) at the point \((\pi/6, 1)\).
- Find the unit vectors that are perpendicular to the tangent line.
- Sketch the curve \(y = 2 \sin x\) and the vectors in parts (a) and (b), all starting at \((\pi/6, 1)\).
Exercise 43
If A, B, and C are the vertices of a triangle, find \(\vec{AB} + \vec{BC} + \vec{CA}\).
Exercise 44
Let C be the point on the line segment AB that is twice as far from B as it is from A. If \(\mathbf{a} = \vec{OA}, \mathbf{b} = \vec{OB},\) and \(\mathbf{c} = \vec{OC}\), show that \(\mathbf{c} = \frac{2}{3}\mathbf{a} + \frac{1}{3}\mathbf{b}\).
Exercise 45
- Draw the vectors \(\mathbf{a} = \langle 3, 2 \rangle, \mathbf{b} = \langle 2, -1 \rangle,\) and \(\mathbf{c} = \langle 7, 1 \rangle\).
- Show, by means of a sketch, that there are scalars s and t such that \(\mathbf{c} = s\mathbf{a} + t\mathbf{b}\).
- Use the sketch to estimate the values of s and t.
- Find the exact values of s and t.
Exercise 46
Suppose that a and b are nonzero vectors that are not parallel and c is any vector in the plane determined by a and b. Give a geometric argument to show that c can be written as \(\mathbf{c} = s\mathbf{a} + t\mathbf{b}\) for suitable scalars s and t. Then give an argument using components.
Exercise 47
If \(\mathbf{r} = \langle x, y, z \rangle\) and \(\mathbf{r}_0 = \langle x_0, y_0, z_0 \rangle\), describe the set of all points \((x, y, z)\) such that \(|\mathbf{r} - \mathbf{r}_0| = 1\).
Exercise 48
If \(\mathbf{r} = \langle x, y \rangle, \mathbf{r}_1 = \langle x_1, y_1 \rangle,\) and \(\mathbf{r}_2 = \langle x_2, y_2 \rangle\), describe the set of all points \((x, y)\) such that \(|\mathbf{r} - \mathbf{r}_1| + |\mathbf{r} - \mathbf{r}_2| = k\), where \(k > |\mathbf{r}_1 - \mathbf{r}_2|\).
Exercise 49
Figure 16 gives a geometric demonstration of Property 2 of vectors. Use components to give an algebraic proof of this fact for the case n = 2.
Exercise 50
Prove Property 5 of vectors algebraically for the case n = 3. Then use similar triangles to give a geometric proof.
Exercise 51
Use vectors to prove that the line joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
Exercise 52
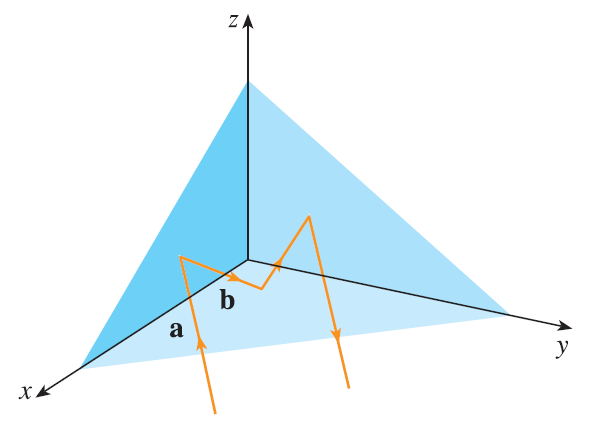
Suppose the three coordinate planes are all mirrored and a light ray given by the vector \(\mathbf{a} = \langle a_1, a_2, a_3 \rangle\) first strikes the xz-plane, as shown in the figure. Use the fact that the angle of incidence equals the angle of reflection to show that the direction of the reflected ray is given by \(\mathbf{b} = \langle a_1, -a_2, a_3 \rangle\). Deduce that, after being reflected by all three mutually perpendicular mirrors, the resulting ray is parallel to the initial ray.