Section 12.3: Dot Product
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 12.3: Dot Product |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 2:12 AM |
Table of contents
- The Dot Product
- Properties of Dot Product
- Geometric Intepretation of Dot Product
- Use of dot product to check perpendicularity of two vectors
- Direction Angles and Direction Cosine
- Projections
- Use of Projection in Physics: Force & Work
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
- Exercise 49
- Exercise 50
- Exercise 51
- Exercise 52
- Exercise 53
- Exercise 54
- Exercise 55
- Exercise 56
- Exercise 57
- Exercise 58
- Exercise 59
- Exercise 60
- Exercise 61
- Exercise 62
- Exercise 63
- Exercise 64
- Exercise 65
The Dot Product
So far we have added two vectors and multiplied a vector by a scalar. The question arises: is it possible to multiply two vectors so that their product is a useful quantity? One such product is the dot product, whose definition follows. Another is the cross product, which is discussed in the next section.
Definition 1 If \(\mathbf{a} = \langle a_1, a_2, a_3 \rangle\) and \(\mathbf{b} = \langle b_1, b_2, b_3 \rangle\), then the dot product of a and b is the number \(\mathbf{a} \cdot \mathbf{b}\) given by \[ \mathbf{a} \cdot \mathbf{b} = a_1b_1 + a_2b_2 + a_3b_3 \]
Thus, to find the dot product of a and b, we multiply corresponding components and add. The result is not a vector. It is a real number, that is, a scalar. For this reason, the dot product is sometimes called the scalar product (or inner product). Although Definition 1 is given for three-dimensional vectors, the dot product of two-dimensional vectors is defined in a similar fashion: \[ \langle a_1, a_2 \rangle \cdot \langle b_1, b_2 \rangle = a_1b_1 + a_2b_2 \]
EXAMPLE 1 \[ \langle 2, 4 \rangle \cdot \langle 3, -1 \rangle = 2(3) + 4(-1) = 2 \] \[ \langle -1, 7, 4 \rangle \cdot \langle 6, 2, -\frac{1}{2} \rangle = (-1)(6) + 7(2) + 4(-\frac{1}{2}) = 6 \] \[ (\mathbf{i} + 2\mathbf{j} - 3\mathbf{k}) \cdot (2\mathbf{j} - \mathbf{k}) = 1(0) + 2(2) + (-3)(-1) = 7 \]
Properties of Dot Product
The dot product obeys many of the laws that hold for ordinary products of real numbers. These are stated in the following theorem.
Properties of the Dot Product 2 If a, b, and c are vectors in \(V_3\) and \(c\) is a scalar, then 1. \(\mathbf{a} \cdot \mathbf{a} = |\mathbf{a}|^2\) 2. \(\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}\) 3. \(\mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c}\) 4. \((c\mathbf{a}) \cdot \mathbf{b} = c(\mathbf{a} \cdot \mathbf{b}) = \mathbf{a} \cdot (c\mathbf{b})\) 5. \(\mathbf{0} \cdot \mathbf{a} = 0\)
These properties are easily proved using Definition 1. For instance, here are the proofs of Properties 1 and 3: 1. \(\mathbf{a} \cdot \mathbf{a} = a_1^2 + a_2^2 + a_3^2 = |\mathbf{a}|^2\) 3. \(\mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) = \langle a_1, a_2, a_3 \rangle \cdot \langle b_1 + c_1, b_2 + c_2, b_3 + c_3 \rangle\) \(= a_1(b_1 + c_1) + a_2(b_2 + c_2) + a_3(b_3 + c_3)\) \(= a_1b_1 + a_1c_1 + a_2b_2 + a_2c_2 + a_3b_3 + a_3c_3\) \(= (a_1b_1 + a_2b_2 + a_3b_3) + (a_1c_1 + a_2c_2 + a_3c_3)\) \(= \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c}\)
The proofs of the remaining properties are left as exercises.
Geometric Intepretation of Dot Product
The dot product \(\mathbf{a} \cdot \mathbf{b}\) can be given a geometric interpretation in terms of the angle \(\theta\) between a and b, which is defined to be the angle between the representations of a and b that start at the origin, where \(0 \le \theta \le \pi\). In other words, \(\theta\) is the angle between the line segments \(\vec{OA}\) and \(\vec{OB}\) in Figure 1.
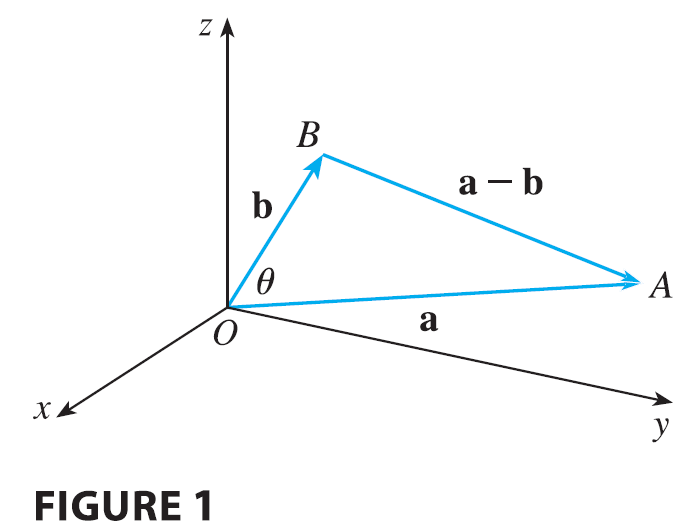
Note that if a and b are parallel vectors, then \(\theta = 0\) or \(\theta = \pi\).
The formula in the following theorem is used by physicists as the definition of the dot product.
Theorem 3 If \(\theta\) is the angle between the vectors a and b, then \[ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos\theta \]
PROOF If we apply the Law of Cosines to triangle OAB in Figure 1, we get \[ |\vec{AB}|^2 = |\vec{OA}|^2 + |\vec{OB}|^2 - 2|\vec{OA}||\vec{OB}|\cos\theta \tag{4} \] (Observe that the Law of Cosines still applies in the limiting cases when \(\theta = 0\) or \(\pi\), or \(\mathbf{a} = \mathbf{0}\) or \(\mathbf{b} = \mathbf{0}\).) But \(|\vec{OA}| = |\mathbf{a}|, |\vec{OB}| = |\mathbf{b}|\), and \(|\vec{AB}| = |\mathbf{a} - \mathbf{b}|\), so Equation 4 becomes \[ |\mathbf{a} - \mathbf{b}|^2 = |\mathbf{a}|^2 + |\mathbf{b}|^2 - 2|\mathbf{a}||\mathbf{b}|\cos\theta \tag{5} \] Using Properties 1, 2, and 3 of the dot product, we can rewrite the left side of this equation as follows: \[ |\mathbf{a} - \mathbf{b}|^2 = (\mathbf{a} - \mathbf{b}) \cdot (\mathbf{a} - \mathbf{b}) = \mathbf{a} \cdot \mathbf{a} - \mathbf{a} \cdot \mathbf{b} - \mathbf{b} \cdot \mathbf{a} + \mathbf{b} \cdot \mathbf{b} = |\mathbf{a}|^2 - 2\mathbf{a} \cdot \mathbf{b} + |\mathbf{b}|^2 \] Therefore Equation 5 gives \[ |\mathbf{a}|^2 - 2\mathbf{a} \cdot \mathbf{b} + |\mathbf{b}|^2 = |\mathbf{a}|^2 + |\mathbf{b}|^2 - 2|\mathbf{a}||\mathbf{b}|\cos\theta \] Thus \[ -2\mathbf{a} \cdot \mathbf{b} = -2|\mathbf{a}||\mathbf{b}|\cos\theta \] or \[ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos\theta \]
EXAMPLE 2 If the vectors a and b have lengths 4 and 6, and the angle between them is \(\pi/3\), find \(\mathbf{a} \cdot \mathbf{b}\).
EXAMPLE 3 Find the angle between the vectors \(\mathbf{a} = \langle 2, 2, -1 \rangle\) and \(\mathbf{b} = \langle 5, -3, 2 \rangle\).
Use of dot product to check perpendicularity of two vectors
Two nonzero vectors a and b are called perpendicular or orthogonal if the angle between them is \(\theta = \pi/2\). Then Theorem 3 gives \[ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos(\pi/2) = 0 \] and conversely if \(\mathbf{a} \cdot \mathbf{b} = 0\), then \(\cos\theta = 0\), so \(\theta = \pi/2\). The zero vector 0 is considered to be perpendicular to all vectors. Therefore we have the following method for determining whether two vectors are orthogonal.
Theorem 7: Two vectors a and b are orthogonal if and only if
\[\mathbf{a} \cdot \mathbf{b} = 0\].
EXAMPLE 4 Show that \(2\mathbf{i} + 2\mathbf{j} - \mathbf{k}\) is perpendicular to \(5\mathbf{i} - 4\mathbf{j} + 2\mathbf{k}\).
Direction Angles and Direction Cosine
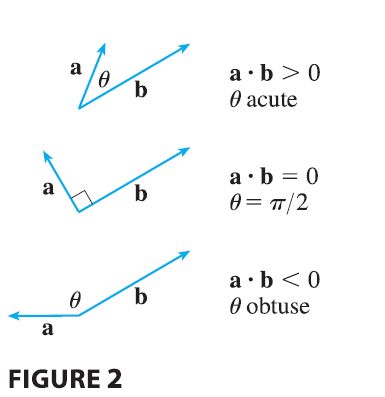
Because \(\cos\theta > 0\) if \(0 \le \theta < \pi/2\) and \(\cos\theta < 0\) if \(\pi/2 < \theta \le \pi\), we see that \(\mathbf{a} \cdot \mathbf{b}\) is positive for \(\theta < \pi/2\) and negative for \(\theta > \pi/2\). We can think of \(\mathbf{a} \cdot \mathbf{b}\) as measuring the extent to which a and b point in the same direction. The dot product \(\mathbf{a} \cdot \mathbf{b}\) is positive if a and b point in the same general direction, 0 if they are perpendicular, and negative if they point in generally opposite directions (see Figure 2). In the extreme case where a and b point in exactly the same direction, we have \(\theta = 0\), so \(\cos\theta = 1\) and \[ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}| \] If a and b point in exactly opposite directions, then we have \(\theta = \pi\) and so \(\cos\theta = -1\) and \(\mathbf{a} \cdot \mathbf{b} = -|\mathbf{a}||\mathbf{b}|\).
Direction Angles and Direction Cosines
The direction angles of a nonzero vector a are the angles \(\alpha, \beta,\) and \(\gamma\) (in the interval \([0, \pi]\)) that a makes with the positive x-, y-, and z-axes, respectively. (See Figure 3.)
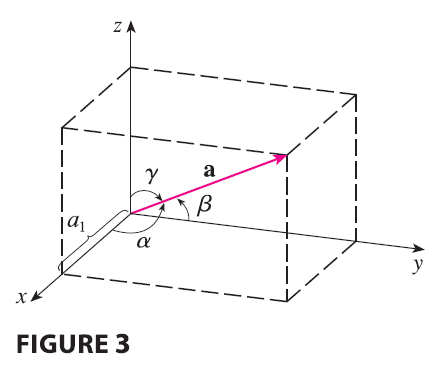
The cosines of these direction angles, \(\cos\alpha, \cos\beta,\) and \(\cos\gamma\), are called the direction cosines of the vector a. Using Corollary 6 with b replaced by i, we obtain \[ \cos\alpha = \frac{\mathbf{a} \cdot \mathbf{i}}{|\mathbf{a}||\mathbf{i}|} = \frac{a_1}{|\mathbf{a}|} \tag{8} \] (This can also be seen directly from Figure 3.) Similarly, we also have \[ \cos\beta = \frac{a_2}{|\mathbf{a}|} \quad \cos\gamma = \frac{a_3}{|\mathbf{a}|} \tag{9} \] By squaring the expressions in Equations 8 and 9 and adding, we see that \[ \cos^2\alpha + \cos^2\beta + \cos^2\gamma = 1 \tag{10} \] We can also use Equations 8 and 9 to write \[ \mathbf{a} = \langle a_1, a_2, a_3 \rangle = \langle |\mathbf{a}|\cos\alpha, |\mathbf{a}|\cos\beta, |\mathbf{a}|\cos\gamma \rangle = |\mathbf{a}|\langle \cos\alpha, \cos\beta, \cos\gamma \rangle \] Therefore \[ \frac{1}{|\mathbf{a}|}\mathbf{a} = \langle \cos\alpha, \cos\beta, \cos\gamma \rangle \tag{11} \] which says that the direction cosines of a are the components of the unit vector in the direction of a.
EXAMPLE 5 Find the direction angles of the vector \(\mathbf{a} = \langle 1, 2, 3 \rangle\).
Projections
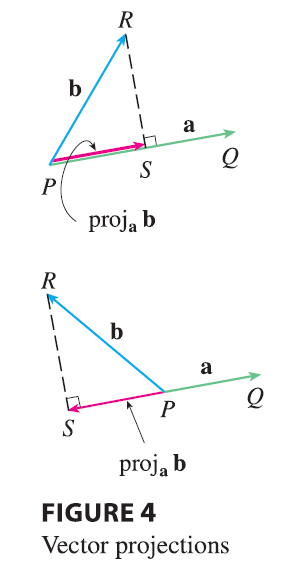
Figure 4 shows representations \(\vec{PQ}\) and \(\vec{PR}\) of two vectors a and b with the same initial point \(P\). If \(S\) is the foot of the perpendicular from \(R\) to the line containing \(\vec{PQ}\), then the vector with representation \(\vec{PS}\) is called the vector projection of b onto a and is denoted by proj\(_\mathbf{a}\)b.
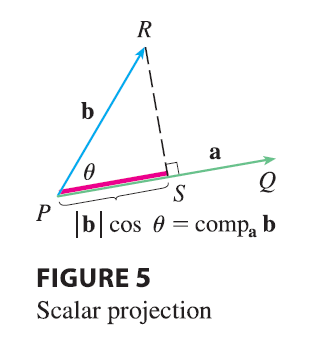
The scalar projection of b onto a (also called the component of b along a) is defined to be the signed magnitude of the vector projection, which is the number \(|\mathbf{b}|\cos\theta\), where \(\theta\) is the angle between a and b. (See Figure 5.) This is denoted by comp\(_\mathbf{a}\)b. Observe that it is negative if \(\pi/2 < \theta \le \pi\). The equation \[ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos\theta = |\mathbf{a}|(|\mathbf{b}|\cos\theta) \] shows that the dot product of a and b can be interpreted as the length of a times the scalar projection of b onto a. Since \[ |\mathbf{b}|\cos\theta = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}|} = \frac{\mathbf{a}}{|\mathbf{a}|} \cdot \mathbf{b} \] the component of b along a can be computed by taking the dot product of b with the unit vector in the direction of a. We summarize these ideas as follows.
Scalar projection of b onto a: \(\text{comp}_\mathbf{a}\mathbf{b} = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}|}\) Vector projection of b onto a: \(\text{proj}_\mathbf{a}\mathbf{b} = \left(\frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}|}\right)\frac{\mathbf{a}}{|\mathbf{a}|} = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}|^2}\mathbf{a}\)
Notice that the vector projection is the scalar projection times the unit vector in the direction of a.
EXAMPLE 6 Find the scalar projection and vector projection of \(\mathbf{b} = \langle 1, 1, 2 \rangle\) onto \(\mathbf{a} = \langle -2, 3, 1 \rangle\).
Use of Projection in Physics: Force & Work
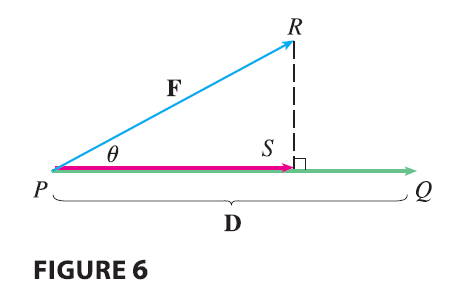
One use of projections occurs in physics in calculating work. We know that the work done by a constant force \(F\) in moving an object through a distance \(d\) as \(W = Fd\), but this applies only when the force is directed along the line of motion of the object. Suppose, however, that the constant force is a vector \(\mathbf{F} = \vec{PR}\) pointing in some other direction, as in Figure 6. If the force moves the object from \(P\) to \(Q\), then the displacement vector is \(\mathbf{D} = \vec{PQ}\). The work done by this force is defined to be the product of the component of the force along D and the distance moved: \[ W = (|\mathbf{F}|\cos\theta)|\mathbf{D}| \] But then, from Theorem 3, we have \[ W = |\mathbf{F}||\mathbf{D}|\cos\theta = \mathbf{F} \cdot \mathbf{D} \tag{12} \] Thus the work done by a constant force F is the dot product \(\mathbf{F} \cdot \mathbf{D}\), where D is the displacement vector.
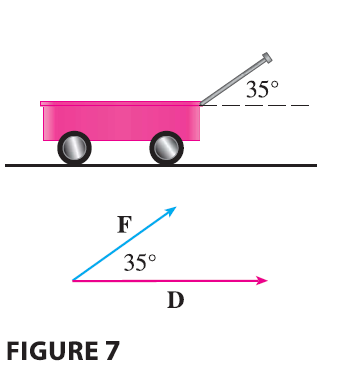
EXAMPLE 7 A wagon is pulled a distance of 100 m along a horizontal path by a constant force of 70 N. The handle of the wagon is held at an angle of \(35^\circ\) above the horizontal. Find the work done by the force.
Exercise 1
Which of the following expressions are meaningful? Which are meaningless? Explain. (a) \((\mathbf{a} \cdot \mathbf{b}) \cdot \mathbf{c}\) (b) \((\mathbf{a} \cdot \mathbf{b})\mathbf{c}\) (c) \(|\mathbf{a}|(\mathbf{b} \cdot \mathbf{c})\) (d) \(\mathbf{a} \cdot (\mathbf{b} + \mathbf{c})\) (e) \(\mathbf{a} \cdot \mathbf{b} + \mathbf{c}\) (f) \(|\mathbf{a}| \cdot (\mathbf{b} + \mathbf{c})\)
Exercise 2
Find \(\mathbf{a} \cdot \mathbf{b}\). \(\mathbf{a} = \langle 5, -2 \rangle, \mathbf{b} = \langle 3, 4 \rangle\)
Exercise 3
Find \(\mathbf{a} \cdot \mathbf{b}\). \(\mathbf{a} = \langle 1.5, 0.4 \rangle, \mathbf{b} = \langle -4, 6 \rangle\)
Exercise 4
Find \(\mathbf{a} \cdot \mathbf{b}\). \(\mathbf{a} = \langle 6, -2, 3 \rangle, \mathbf{b} = \langle 2, 5, -1 \rangle\)
Exercise 5
Find \(\mathbf{a} \cdot \mathbf{b}\). \(\mathbf{a} = \langle 4, 1, \frac{1}{4} \rangle, \mathbf{b} = \langle 6, -3, -8 \rangle\)
Exercise 6
Find \(\mathbf{a} \cdot \mathbf{b}\). \(\mathbf{a} = \langle p, -p, 2p \rangle, \mathbf{b} = \langle 2q, q, -q \rangle\)
Exercise 7
Find \(\mathbf{a} \cdot \mathbf{b}\). \(\mathbf{a} = 2\mathbf{i} + \mathbf{j}, \mathbf{b} = \mathbf{i} - \mathbf{j} + \mathbf{k}\)
Exercise 8
Find \(\mathbf{a} \cdot \mathbf{b}\). \(\mathbf{a} = 3\mathbf{i} + 2\mathbf{j} - \mathbf{k}, \mathbf{b} = 4\mathbf{i} + 5\mathbf{k}\)
Exercise 9
Find \(\mathbf{a} \cdot \mathbf{b}\). \(|\mathbf{a}| = 7, |\mathbf{b}| = 4\), the angle between a and b is \(30^\circ\)
Exercise 10
Find \(\mathbf{a} \cdot \mathbf{b}\). \(|\mathbf{a}| = 80, |\mathbf{b}| = 50\), the angle between a and b is \(3\pi/4\)
Exercise 11
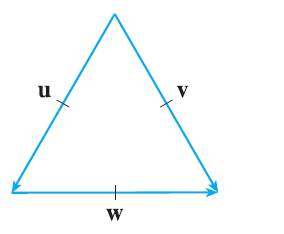
If u is a unit vector, find \(\mathbf{u} \cdot \mathbf{v}\) and \(\mathbf{u} \cdot \mathbf{w}\). (A diagram with an equilateral triangle with side length 1 is shown, with vectors u, v, w forming the sides).
Exercise 12
If u is a unit vector, find \(\mathbf{u} \cdot \mathbf{v}\) and \(\mathbf{u} \cdot \mathbf{w}\). (A diagram with a square with side length 1 is shown, with vectors u, v, w).
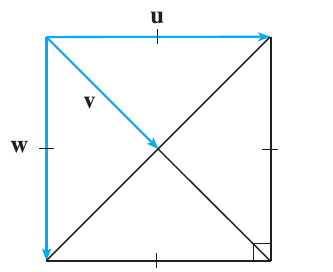
Exercise 13
- Show that \(\mathbf{i} \cdot \mathbf{j} = \mathbf{j} \cdot \mathbf{k} = \mathbf{k} \cdot \mathbf{i} = 0\).
- Show that \(\mathbf{i} \cdot \mathbf{i} = \mathbf{j} \cdot \mathbf{j} = \mathbf{k} \cdot \mathbf{k} = 1\).
Exercise 14
A street vendor sells \(a\) hamburgers, \(b\) hot dogs, and \(c\) soft drinks on a given day. He charges $2 for a hamburger, $1.50 for a hot dog, and $1 for a soft drink. If \(\mathbf{A} = \langle a, b, c \rangle\) and \(\mathbf{P} = \langle 2, 1.5, 1 \rangle\), what is the meaning of the dot product \(\mathbf{A} \cdot \mathbf{P}\)?
Exercise 15
Find the angle between the vectors. (First find an exact expression and then approximate to the nearest degree.) \(\mathbf{a} = \langle 4, 3 \rangle, \mathbf{b} = \langle 2, -1 \rangle\)
Exercise 16
Find the angle between the vectors. (First find an exact expression and then approximate to the nearest degree.) \(\mathbf{a} = \langle -2, 5 \rangle, \mathbf{b} = \langle 5, 12 \rangle\)
Exercise 17
Find the angle between the vectors. (First find an exact expression and then approximate to the nearest degree.) \(\mathbf{a} = \langle 1, -4, 1 \rangle, \mathbf{b} = \langle 0, 2, -2 \rangle\)
Exercise 18
Find the angle between the vectors. (First find an exact expression and then approximate to the nearest degree.) \(\mathbf{a} = \langle -1, 3, 4 \rangle, \mathbf{b} = \langle 5, 2, 1 \rangle\)
Exercise 19
Find the angle between the vectors. (First find an exact expression and then approximate to the nearest degree.) \(\mathbf{a} = 4\mathbf{i} - 3\mathbf{j} + \mathbf{k}, \mathbf{b} = 2\mathbf{i} - \mathbf{k}\)
Exercise 20
Find the angle between the vectors. (First find an exact expression and then approximate to the nearest degree.) \(\mathbf{a} = 8\mathbf{i} - \mathbf{j} + 4\mathbf{k}, \mathbf{b} = 4\mathbf{j} + 2\mathbf{k}\)
Exercise 21
Find, correct to the nearest degree, the three angles of the triangle with the given vertices. \(P(2, 0), Q(0, 3), R(3, 4)\)
Exercise 22
Find, correct to the nearest degree, the three angles of the triangle with the given vertices. \(A(1, 0, -1), B(3, -2, 0), C(1, 3, 3)\)
Exercise 23
Determine whether the given vectors are orthogonal, parallel, or neither. (a) \(\mathbf{a} = \langle 9, 3 \rangle, \mathbf{b} = \langle -2, 6 \rangle\) (b) \(\mathbf{a} = \langle 4, 5, -2 \rangle, \mathbf{b} = \langle 3, -1, 5 \rangle\) (c) \(\mathbf{a} = -8\mathbf{i} + 12\mathbf{j} + 4\mathbf{k}, \mathbf{b} = 6\mathbf{i} - 9\mathbf{j} - 3\mathbf{k}\) (d) \(\mathbf{a} = 3\mathbf{i} - \mathbf{j} + 3\mathbf{k}, \mathbf{b} = 5\mathbf{i} + 9\mathbf{j} - 2\mathbf{k}\)
Exercise 24
Determine whether the given vectors are orthogonal, parallel, or neither. (a) \(\mathbf{u} = \langle -5, 4, -2 \rangle, \mathbf{v} = \langle 3, 4, -1 \rangle\) (b) \(\mathbf{u} = 9\mathbf{i} - 6\mathbf{j} + 3\mathbf{k}, \mathbf{v} = -6\mathbf{i} + 4\mathbf{j} - 2\mathbf{k}\) (c) \(\mathbf{u} = \langle c, c, c \rangle, \mathbf{v} = \langle c, 0, -c \rangle\)
Exercise 25
Use vectors to decide whether the triangle with vertices \(P(1, -3, -2), Q(2, 0, -4),\) and \(R(6, -2, -5)\) is right-angled.
Exercise 26
Find the values of \(x\) such that the angle between the vectors \(\langle 2, 1, -1 \rangle\) and \(\langle 1, x, 0 \rangle\) is \(45^\circ\).
Exercise 27
Find a unit vector that is orthogonal to both \(\mathbf{i} + \mathbf{j}\) and \(\mathbf{i} + \mathbf{k}\).
Exercise 28
Find two unit vectors that make an angle of \(60^\circ\) with \(\mathbf{v} = \langle 3, 4 \rangle\).
Exercise 29
Find the acute angle between the lines. \(2x - y = 3, 3x + y = 7\)
Exercise 30
Find the acute angle between the lines. \(x + 2y = 7, 5x - y = 2\)
Exercise 31
Find the acute angles between the curves at their points of intersection. (The angle between two curves is the angle between their tangent lines at the point of intersection.) \(y = x^2, y = x^3\)
Exercise 32
Find the acute angles between the curves at their points of intersection. (The angle between two curves is the angle between their tangent lines at the point of intersection.) \(y = \sin x, y = \cos x, 0 \le x \le \pi/2\)
Exercise 33
Find the direction cosines and direction angles of the vector. (Give the direction angles correct to the nearest degree.) \(\langle 2, 1, 2 \rangle\)
Exercise 34
Find the direction cosines and direction angles of the vector. (Give the direction angles correct to the nearest degree.) \(\langle 6, 3, -2 \rangle\)
Exercise 35
Find the direction cosines and direction angles of the vector. (Give the direction angles correct to the nearest degree.) \(\mathbf{i} - 2\mathbf{j} - 3\mathbf{k}\)
Exercise 36
Find the direction cosines and direction angles of the vector. (Give the direction angles correct to the nearest degree.) \(\langle 1, 1, 1 \rangle\)
Exercise 37
Find the direction cosines and direction angles of the vector. (Give the direction angles correct to the nearest degree.) \(\langle c, c, c \rangle\), where \(c > 0\)
Exercise 38
If a vector has direction angles \(\alpha = \pi/4\) and \(\beta = \pi/3\), find the third direction angle \(\gamma\).
Exercise 39
Find the scalar and vector projections of b onto a. \(\mathbf{a} = \langle -5, 12 \rangle, \mathbf{b} = \langle 4, 6 \rangle\)
Exercise 40
Find the scalar and vector projections of b onto a. \(\mathbf{a} = \langle 1, 4 \rangle, \mathbf{b} = \langle 2, 3 \rangle\)
Exercise 41
Find the scalar and vector projections of b onto a. \(\mathbf{a} = \langle 4, 7, -4 \rangle, \mathbf{b} = \langle 3, -1, 1 \rangle\)
Exercise 42
Find the scalar and vector projections of b onto a. \(\mathbf{a} = \langle -1, 4, 8 \rangle, \mathbf{b} = \langle 12, 1, 2 \rangle\)
Exercise 43
Find the scalar and vector projections of b onto a. \(\mathbf{a} = 3\mathbf{i} - 3\mathbf{j} + \mathbf{k}, \mathbf{b} = 2\mathbf{i} + 4\mathbf{j} - \mathbf{k}\)
Exercise 44
Find the scalar and vector projections of b onto a. \(\mathbf{a} = \mathbf{i} + 2\mathbf{j} + 3\mathbf{k}, \mathbf{b} = 5\mathbf{i} - \mathbf{k}\)
Exercise 45
Show that the vector \(\text{orth}_\mathbf{a}\mathbf{b} = \mathbf{b} - \text{proj}_\mathbf{a}\mathbf{b}\) is orthogonal to a. (It is called an orthogonal projection of b.)
Exercise 46
For the vectors in Exercise 40, find \(\text{orth}_\mathbf{a}\mathbf{b}\) and illustrate by drawing the vectors a, b, \(\text{proj}_\mathbf{a}\mathbf{b}\), and \(\text{orth}_\mathbf{a}\mathbf{b}\).
Exercise 47
If \(\mathbf{a} = \langle 3, 0, -1 \rangle\), find a vector b such that \(\text{comp}_\mathbf{a}\mathbf{b} = 2\).
Exercise 48
Suppose that a and b are nonzero vectors. (a) Under what circumstances is \(\text{comp}_\mathbf{a}\mathbf{b} = \text{comp}_\mathbf{b}\mathbf{a}\)? (b) Under what circumstances is \(\text{proj}_\mathbf{a}\mathbf{b} = \text{proj}_\mathbf{b}\mathbf{a}\)?
Exercise 49
Find the work done by a force \(\mathbf{F} = 8\mathbf{i} - 6\mathbf{j} + 9\mathbf{k}\) that moves an object from the point \((0, 10, 8)\) to the point \((6, 12, 20)\) along a straight line. The distance is measured in meters and the force in newtons.
Exercise 50
A tow truck drags a stalled car along a road. The chain makes an angle of \(30^\circ\) with the road and the tension in the chain is 1500 N. How much work is done by the truck in pulling the car 1 km?
Exercise 51
A sled is pulled along a level path through snow by a rope. A 30-lb force acting at an angle of \(40^\circ\) above the horizontal moves the sled 80 ft. Find the work done by the force.
Exercise 52
A boat sails south with the help of a wind blowing in the direction S36°E with magnitude 400 lb. Find the work done by the wind as the boat moves 120 ft.
Exercise 53
Use a scalar projection to show that the distance from a point \(P_1(x_1, y_1)\) to the line \(ax + by + c = 0\) is \[ \frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}} \] Use this formula to find the distance from the point \((-2, 3)\) to the line \(3x - 4y + 5 = 0\).
Exercise 54
If \(\mathbf{r} = \langle x, y, z \rangle, \mathbf{a} = \langle a_1, a_2, a_3 \rangle,\) and \(\mathbf{b} = \langle b_1, b_2, b_3 \rangle\), show that the vector equation \((\mathbf{r} - \mathbf{a}) \cdot (\mathbf{r} - \mathbf{b}) = 0\) represents a sphere, and find its center and radius.
Exercise 55
Find the angle between a diagonal of a cube and one of its edges.
Exercise 56
Find the angle between a diagonal of a cube and a diagonal of one of its faces.
Exercise 57
A molecule of methane, CH\(_4\), is structured with the four hydrogen atoms at the vertices of a regular tetrahedron and the carbon atom at the centroid. The bond angle is the angle formed by the H-C-H combination; it is the angle between the lines that join the carbon atom to two of the hydrogen atoms. Show that the bond angle is about \(109.5^\circ\). [Hint: Take the vertices of the tetrahedron to be the points (1, 0, 0), (0, 1, 0), (0, 0, 1), and (1, 1, 1), as shown in the figure. Then the centroid is \((\frac{1}{2}, \frac{1}{2}, \frac{1}{2})\).]
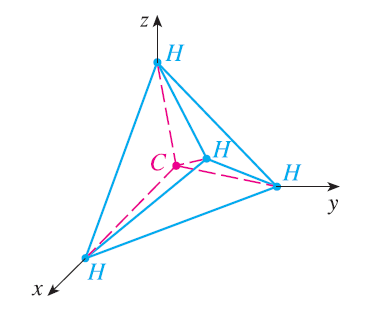
Exercise 58
If \(\mathbf{c} = |\mathbf{a}|\mathbf{b} + |\mathbf{b}|\mathbf{a}\), where a, b, and c are all nonzero vectors, show that c bisects the angle between a and b.
Exercise 59
Prove Properties 2, 4, and 5 of the dot product (Theorem 2).
Exercise 60
Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular.
Exercise 61
Use Theorem 3 to prove the Cauchy-Schwarz Inequality: \(|\mathbf{a} \cdot \mathbf{b}| \le |\mathbf{a}||\mathbf{b}|\)
Exercise 62
The Triangle Inequality for vectors is \(|\mathbf{a} + \mathbf{b}| \le |\mathbf{a}| + |\mathbf{b}|\) (a) Give a geometric interpretation of the Triangle Inequality. (b) Use the Cauchy-Schwarz Inequality from Exercise 61 to prove the Triangle Inequality. [Hint: Use the fact that \(|\mathbf{a} + \mathbf{b}|^2 = (\mathbf{a} + \mathbf{b}) \cdot (\mathbf{a} + \mathbf{b})\) and use Property 3 of the dot product.]
Exercise 63
The Parallelogram Law states that \(|\mathbf{a} + \mathbf{b}|^2 + |\mathbf{a} - \mathbf{b}|^2 = 2|\mathbf{a}|^2 + 2|\mathbf{b}|^2\) (a) Give a geometric interpretation of the Parallelogram Law. (b) Prove the Parallelogram Law. (See the hint in Exercise 62.)
Exercise 64
Show that if \(\mathbf{u} + \mathbf{v}\) and \(\mathbf{u} - \mathbf{v}\) are orthogonal, then the vectors u and v must have the same length.
Exercise 65
If \(\theta\) is the angle between vectors a and b, show that \(\text{proj}_\mathbf{a}(\text{proj}_\mathbf{a}\mathbf{b}) = (\mathbf{a} \cdot \mathbf{b})\cos^2\theta\)