Section 12.4: Cross Product
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 12.4: Cross Product |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 3:57 AM |
Table of contents
- The Cross Product
- Example: Cross product with parallel vectors
- Cross product is perpendicular to the plane
- Right Hand Rule
- Cross Product & Area of parallelogram
- Example exercise
- Example Exercise
- Some common identities
- Triple Products
- Vector Triple Product
- Torque
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
- Exercise 49
- Exercise 50
- Exercise 51
- Exercise 52
- Exercise 53
- Exercise 54
The Cross Product
Given two nonzero vectors \(\mathbf{a} = \langle a_1, a_2, a_3 \rangle\) and \(\mathbf{b} = \langle b_1, b_2, b_3 \rangle\), it is very useful to be able to find a nonzero vector c that is perpendicular to both a and b. If \(\mathbf{c} = \langle c_1, c_2, c_3 \rangle\) is such a vector, then \(\mathbf{a} \cdot \mathbf{c} = 0\) and \(\mathbf{b} \cdot \mathbf{c} = 0\) and so \[ a_1c_1 + a_2c_2 + a_3c_3 = 0 \tag{1} \] \[ b_1c_1 + b_2c_2 + b_3c_3 = 0 \tag{2} \] To eliminate \(c_3\) we multiply (1) by \(b_3\) and (2) by \(a_3\) and subtract: \[ (a_1b_3 - a_3b_1)c_1 + (a_2b_3 - a_3b_2)c_2 = 0 \tag{3} \] Equation 3 has the form \(pc_1 + qc_2 = 0\), for which an obvious solution is \(c_1 = q\) and \(c_2 = -p\). So a solution of (3) is \[ c_1 = a_2b_3 - a_3b_2 \qquad c_2 = a_3b_1 - a_1b_3 \] Substituting these values into (1) and (2), we then get \[ c_3 = a_1b_2 - a_2b_1 \] This means that a vector perpendicular to both a and b is \[ \mathbf{c} = \langle c_1, c_2, c_3 \rangle = \langle a_2b_3 - a_3b_2, a_3b_1 - a_1b_3, a_1b_2 - a_2b_1 \rangle \] The resulting vector is called the cross product of a and b and is denoted by \(\mathbf{a} \times \mathbf{b}\).
Definition 4 If \(\mathbf{a} = \langle a_1, a_2, a_3 \rangle\) and \(\mathbf{b} = \langle b_1, b_2, b_3 \rangle\), then the cross product of a and b is the vector \[ \mathbf{a} \times \mathbf{b} = \langle a_2b_3 - a_3b_2, a_3b_1 - a_1b_3, a_1b_2 - a_2b_1 \rangle \]
Notice that the cross product \(\mathbf{a} \times \mathbf{b}\) of two vectors a and b, unlike the dot product, is a vector. For this reason it is also called the vector product. Note that \(\mathbf{a} \times \mathbf{b}\) is defined only when a and b are three-dimensional vectors.
In order to make Definition 4 easier to remember, we use the notation of determinants. A determinant of order 2 is defined by \[ \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc \] (Multiply across the diagonals and subtract.) For example, \[ \begin{vmatrix} 2 & 1 \\ -6 & 4 \end{vmatrix} = 2(4) - 1(-6) = 14 \] A determinant of order 3 can be defined in terms of second-order determinants as follows: \[ \begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix} = a_1 \begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix} - a_2 \begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix} + a_3 \begin{vmatrix} b_1 & b_2 \\ c_1 & c_2 \end{vmatrix} \tag{5} \] Observe that each term on the right side of Equation 5 involves a number \(a_i\) in the first row of the determinant, and \(a_i\) is multiplied by the second-order determinant obtained from the left side by deleting the row and column in which \(a_i\) appears. Notice also the minus sign in the second term. For example, \[ \begin{vmatrix} 1 & 2 & -1 \\ 3 & 0 & 1 \\ -5 & 4 & 2 \end{vmatrix} = 1 \begin{vmatrix} 0 & 1 \\ 4 & 2 \end{vmatrix} - 2 \begin{vmatrix} 3 & 1 \\ -5 & 2 \end{vmatrix} + (-1) \begin{vmatrix} 3 & 0 \\ -5 & 4 \end{vmatrix} \] \[ = 1(0 - 4) - 2(6 - (-5)) + (-1)(12 - 0) = -4 - 22 - 12 = -38 \] If we now rewrite Definition 4 using second-order determinants and the standard basis vectors i, j, and k, we see that the cross product of the vectors \(\mathbf{a} = a_1\mathbf{i} + a_2\mathbf{j} + a_3\mathbf{k}\) and \(\mathbf{b} = b_1\mathbf{i} + b_2\mathbf{j} + b_3\mathbf{k}\) is \[ \mathbf{a} \times \mathbf{b} = \begin{vmatrix} a_2 & a_3 \\ b_2 & b_3 \end{vmatrix} \mathbf{i} - \begin{vmatrix} a_1 & a_3 \\ b_1 & b_3 \end{vmatrix} \mathbf{j} + \begin{vmatrix} a_1 & a_2 \\ b_1 & b_2 \end{vmatrix} \mathbf{k} \tag{6} \] In view of the similarity between Equations 5 and 6, we often write \[ \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} \tag{7} \] Although the first row of the symbolic determinant in Equation 7 consists of vectors, if we expand it as if it were an ordinary determinant using the rule in Equation 5, we obtain Equation 6. The symbolic formula in Equation 7 is probably the easiest way of remembering and computing cross products.
EXAMPLE 1 If \(\mathbf{a} = \langle 1, 3, 4 \rangle\) and \(\mathbf{b} = \langle 2, 7, -5 \rangle\), then \[ \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 3 & 4 \\ 2 & 7 & -5 \end{vmatrix} = \begin{vmatrix} 3 & 4 \\ 7 & -5 \end{vmatrix} \mathbf{i} - \begin{vmatrix} 1 & 4 \\ 2 & -5 \end{vmatrix} \mathbf{j} + \begin{vmatrix} 1 & 3 \\ 2 & 7 \end{vmatrix} \mathbf{k} \] \[ = (-15 - 28)\mathbf{i} - (-5 - 8)\mathbf{j} + (7 - 6)\mathbf{k} = -43\mathbf{i} + 13\mathbf{j} + \mathbf{k} \]
Example: Cross product with parallel vectors
EXAMPLE 2 Show that \(\mathbf{a} \times \mathbf{a} = \mathbf{0}\) for any vector a in \(V_3\).
Cross product is perpendicular to the plane
We constructed the cross product \(\mathbf{a} \times \mathbf{b}\) so that it would be perpendicular to both a and b. This is one of the most important properties of a cross product, so let’s emphasize and verify it in the following theorem and give a formal proof.
Theorem 8 The vector \(\mathbf{a} \times \mathbf{b}\) is orthogonal to both a and b.
PROOF In order to show that \(\mathbf{a} \times \mathbf{b}\) is orthogonal to a, we compute their dot product as follows: \[ (\mathbf{a} \times \mathbf{b}) \cdot \mathbf{a} = \begin{vmatrix} a_2 & a_3 \\ b_2 & b_3 \end{vmatrix} a_1 - \begin{vmatrix} a_1 & a_3 \\ b_1 & b_3 \end{vmatrix} a_2 + \begin{vmatrix} a_1 & a_2 \\ b_1 & b_2 \end{vmatrix} a_3 \] \[ = a_1(a_2b_3 - a_3b_2) - a_2(a_1b_3 - a_3b_1) + a_3(a_1b_2 - a_2b_1) \] \[ = a_1a_2b_3 - a_1a_3b_2 - a_1a_2b_3 + a_2a_3b_1 + a_1a_3b_2 - a_2a_3b_1 = 0 \] A similar computation shows that \((\mathbf{a} \times \mathbf{b}) \cdot \mathbf{b} = 0\). Therefore \(\mathbf{a} \times \mathbf{b}\) is orthogonal to both a and b.
Right Hand Rule
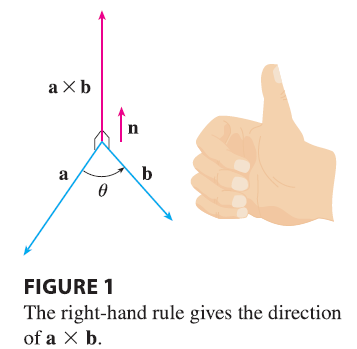
If a and b are represented by directed line segments with the same initial point (as in Figure 1), then Theorem 8 says that the cross product \(\mathbf{a} \times \mathbf{b}\) points in a direction perpendicular to the plane through a and b. It turns out that the direction of \(\mathbf{a} \times \mathbf{b}\) is given by the right-hand rule: if the fingers of your right hand curl in the direction of a rotation (through an angle less than \(180^\circ\)) from a to b, then your thumb points in the direction of \(\mathbf{a} \times \mathbf{b}\).
Now that we know the direction of the vector \(\mathbf{a} \times \mathbf{b}\), the remaining thing we need to complete its geometric description is its length \(|\mathbf{a} \times \mathbf{b}|\). This is given by the following theorem.
Theorem 9 If \(\theta\) is the angle between a and b (so \(0 \le \theta \le \pi\)), then \[ |\mathbf{a} \times \mathbf{b}| = |\mathbf{a}||\mathbf{b}|\sin\theta \]
PROOF From the definitions of the cross product and length of a vector, we have \[ |\mathbf{a} \times \mathbf{b}|^2 = (a_2b_3 - a_3b_2)^2 + (a_3b_1 - a_1b_3)^2 + (a_1b_2 - a_2b_1)^2 \] \[ = a_2^2b_3^2 - 2a_2a_3b_2b_3 + a_3^2b_2^2 + a_3^2b_1^2 - 2a_1a_3b_1b_3 + a_1^2b_3^2 + a_1^2b_2^2 - 2a_1a_2b_1b_2 + a_2^2b_1^2 \] \[ = (a_1^2 + a_2^2 + a_3^2)(b_1^2 + b_2^2 + b_3^2) - (a_1b_1 + a_2b_2 + a_3b_3)^2 \] \[ = |\mathbf{a}|^2|\mathbf{b}|^2 - (\mathbf{a} \cdot \mathbf{b})^2 = |\mathbf{a}|^2|\mathbf{b}|^2 - |\mathbf{a}|^2|\mathbf{b}|^2\cos^2\theta \quad (\text{by Theorem 12.3.3}) \] \[ = |\mathbf{a}|^2|\mathbf{b}|^2(1 - \cos^2\theta) = |\mathbf{a}|^2|\mathbf{b}|^2\sin^2\theta \] Taking square roots and observing that \(\sqrt{\sin^2\theta} = \sin\theta\) because \(\sin\theta \ge 0\) when \(0 \le \theta \le \pi\), we have \[ |\mathbf{a} \times \mathbf{b}| = |\mathbf{a}||\mathbf{b}|\sin\theta \] Since a vector is completely determined by its magnitude and direction, we can now say that \(\mathbf{a} \times \mathbf{b}\) is the vector that is perpendicular to both a and b, whose orientation is determined by the right-hand rule, and whose length is \(|\mathbf{a}||\mathbf{b}|\sin\theta\). In fact, that is exactly how physicists define \(\mathbf{a} \times \mathbf{b}\).
Corollary 10 Two nonzero vectors a and b are parallel if and only if \[ \mathbf{a} \times \mathbf{b} = \mathbf{0} \]
PROOF Two nonzero vectors a and b are parallel if and only if \(\theta = 0\) or \(\pi\). In either case \(\sin\theta = 0\), so \(|\mathbf{a} \times \mathbf{b}| = 0\) and therefore \(\mathbf{a} \times \mathbf{b} = \mathbf{0}\).
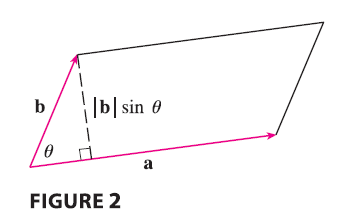
The geometric interpretation of Theorem 9 can be seen by looking at Figure 2. If a and b are represented by directed line segments with the same initial point, then they determine a parallelogram with base \(|\mathbf{a}|\), altitude \(|\mathbf{b}|\sin\theta\), and area \[ A = |\mathbf{a}|(|\mathbf{b}|\sin\theta) = |\mathbf{a} \times \mathbf{b}| \] Thus we have the following way of interpreting the magnitude of a cross product.
Cross Product & Area of parallelogram
The length of the cross product \(\mathbf{a} \times \mathbf{b}\) is equal to the area of the parallelogram determined by a and b.
Example exercise
EXAMPLE 3 Find a vector perpendicular to the plane that passes through the points \(P(1, 4, 6), Q(-2, 5, -1),\) and \(R(1, -1, 1)\).
Example Exercise
EXAMPLE 4 Find the area of the triangle with vertices \(P(1, 4, 6), Q(-2, 5, -1),\) and \(R(1, -1, 1)\).
Some common identities
If we apply Theorems 8 and 9 to the standard basis vectors i, j, and k using \(\theta = \pi/2\), we obtain \[ \mathbf{i} \times \mathbf{j} = \mathbf{k} \qquad \mathbf{j} \times \mathbf{k} = \mathbf{i} \qquad \mathbf{k} \times \mathbf{i} = \mathbf{j} \] \[ \mathbf{j} \times \mathbf{i} = -\mathbf{k} \qquad \mathbf{k} \times \mathbf{j} = -\mathbf{i} \qquad \mathbf{i} \times \mathbf{k} = -\mathbf{j} \] Observe that \[ \mathbf{i} \times \mathbf{j} \ne \mathbf{j} \times \mathbf{i} \] Thus the cross product is not commutative. Also \[ \mathbf{i} \times (\mathbf{i} \times \mathbf{j}) = \mathbf{i} \times \mathbf{k} = -\mathbf{j} \] whereas \[ (\mathbf{i} \times \mathbf{i}) \times \mathbf{j} = \mathbf{0} \times \mathbf{j} = \mathbf{0} \] So the associative law for multiplication does not usually hold; that is, in general, \[ (\mathbf{a} \times \mathbf{b}) \times \mathbf{c} \ne \mathbf{a} \times (\mathbf{b} \times \mathbf{c}) \] However, some of the usual laws of algebra do hold for cross products. The following theorem summarizes the properties of vector products.
Properties of the Cross Product 11 If a, b, and c are vectors and \(c\) is a scalar, then 1. \(\mathbf{a} \times \mathbf{b} = -\mathbf{b} \times \mathbf{a}\) 2. \((c\mathbf{a}) \times \mathbf{b} = c(\mathbf{a} \times \mathbf{b}) = \mathbf{a} \times (c\mathbf{b})\) 3. \(\mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c}\) 4. \((\mathbf{a} + \mathbf{b}) \times \mathbf{c} = \mathbf{a} \times \mathbf{c} + \mathbf{b} \times \mathbf{c}\) 5. \(\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = (\mathbf{a} \times \mathbf{b}) \cdot \mathbf{c}\) 6. \(\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) = (\mathbf{a} \cdot \mathbf{c})\mathbf{b} - (\mathbf{a} \cdot \mathbf{b})\mathbf{c}\)
These properties can be proved by writing the vectors in terms of their components and using the definition of a cross product. We give the proof of Property 5 and leave the remaining proofs as exercises.
PROOF OF PROPERTY 5 If \(\mathbf{a} = \langle a_1, a_2, a_3 \rangle, \mathbf{b} = \langle b_1, b_2, b_3 \rangle,\) and \(\mathbf{c} = \langle c_1, c_2, c_3 \rangle\), then \[ \mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = a_1(b_2c_3 - b_3c_2) + a_2(b_3c_1 - b_1c_3) + a_3(b_1c_2 - b_2c_1) \tag{12} \] \[ = a_1b_2c_3 - a_1b_3c_2 + a_2b_3c_1 - a_2b_1c_3 + a_3b_1c_2 - a_3b_2c_1 \] \[ = (a_2b_3 - a_3b_2)c_1 + (a_3b_1 - a_1b_3)c_2 + (a_1b_2 - a_2b_1)c_3 \] \[ = (\mathbf{a} \times \mathbf{b}) \cdot \mathbf{c} \]
Triple Products
The product \(\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})\) that occurs in Property 5 is called the scalar triple product of the vectors a, b, and c. Notice from Equation 12 that we can write the scalar triple product as a determinant: \[ \mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = \begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix} \tag{13} \]
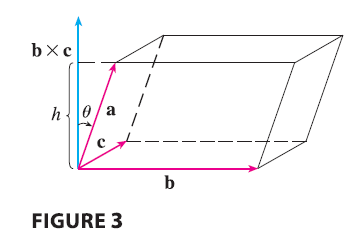
The geometric significance of the scalar triple product can be seen by considering the parallelepiped determined by the vectors a, b, and c. (See Figure 3.) The area of the base parallelogram is \(A = |\mathbf{b} \times \mathbf{c}|\). If \(\theta\) is the angle between a and \(\mathbf{b} \times \mathbf{c}\), then the height \(h\) of the parallelepiped is \(h = |\mathbf{a}||\cos\theta|\). (We must use \(|\cos\theta|\) instead of \(\cos\theta\) in case \(\theta > \pi/2\).) Therefore the volume of the parallelepiped is \[ V = Ah = |\mathbf{b} \times \mathbf{c}||\mathbf{a}||\cos\theta| = |\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})| \] Thus we have proved the following formula.
The volume of the parallelepiped determined by the vectors a, b, and c is the magnitude of their scalar triple product: \[ V = |\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})| \tag{14} \]
If we use the formula in (14) and discover that the volume of the parallelepiped determined by a, b, and c is 0, then the vectors must lie in the same plane; that is, they are coplanar.
EXAMPLE 5 Use the scalar triple product to show that the vectors \(\mathbf{a} = \langle 1, 4, -7 \rangle, \mathbf{b} = \langle 2, -1, 4 \rangle,\) and \(\mathbf{c} = \langle 0, -9, 18 \rangle\) are coplanar.
Vector Triple Product
The product \(\mathbf{a} \times (\mathbf{b} \times \mathbf{c})\) that occurs in Property 6 is called the vector triple product of a, b, and c.
Torque
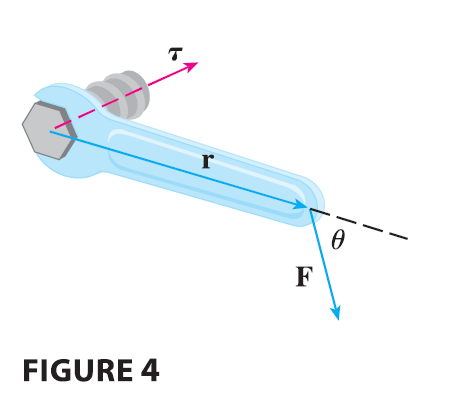
The idea of a cross product occurs often in physics. In particular, we consider a force F acting on a rigid body at a point given by a position vector r. The torque \(\mathbf{\tau}\) (relative to the origin) is defined to be the cross product of the position and force vectors \[ \mathbf{\tau} = \mathbf{r} \times \mathbf{F} \] and measures the tendency of the body to rotate about the origin. The direction of the torque vector indicates the axis of rotation. According to Theorem 9, the magnitude of the torque vector is \[ |\mathbf{\tau}| = |\mathbf{r} \times \mathbf{F}| = |\mathbf{r}||\mathbf{F}|\sin\theta \] where \(\theta\) is the angle between the position and force vectors. Observe that the only component of F that can cause a rotation is the one perpendicular to r, that is, \(|\mathbf{F}|\sin\theta\). The magnitude of the torque is equal to the area of the parallelogram determined by r and F.
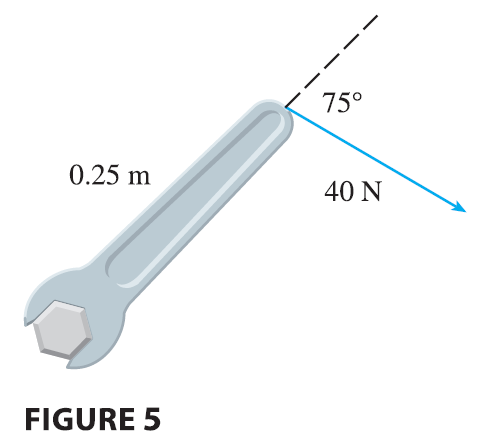
EXAMPLE 6 A bolt is tightened by applying a 40-N force to a 0.25-m wrench as shown in Figure 5. Find the magnitude of the torque about the center of the bolt.
Exercise 1
Find the cross product \(\mathbf{a} \times \mathbf{b}\) and verify that it is orthogonal to both a and b. \(\mathbf{a} = \langle 2, 3, 0 \rangle, \mathbf{b} = \langle 1, 0, 5 \rangle\)
Exercise 2
Find the cross product \(\mathbf{a} \times \mathbf{b}\) and verify that it is orthogonal to both a and b. \(\mathbf{a} = \langle 4, 3, -2 \rangle, \mathbf{b} = \langle 2, -1, 1 \rangle\)
Exercise 3
Find the cross product \(\mathbf{a} \times \mathbf{b}\) and verify that it is orthogonal to both a and b. \(\mathbf{a} = 2\mathbf{j} - 4\mathbf{k}, \mathbf{b} = -\mathbf{i} + 3\mathbf{j} + \mathbf{k}\)
Exercise 4
Find the cross product \(\mathbf{a} \times \mathbf{b}\) and verify that it is orthogonal to both a and b. \(\mathbf{a} = 3\mathbf{i} + 3\mathbf{j} - 3\mathbf{k}, \mathbf{b} = 3\mathbf{i} - 3\mathbf{j} + 3\mathbf{k}\)
Exercise 5
Find the cross product \(\mathbf{a} \times \mathbf{b}\) and verify that it is orthogonal to both a and b. \(\mathbf{a} = \frac{1}{2}\mathbf{i} + \frac{1}{3}\mathbf{j} + \frac{1}{4}\mathbf{k}, \mathbf{b} = \mathbf{i} + 2\mathbf{j} - 3\mathbf{k}\)
Exercise 6
Find the cross product \(\mathbf{a} \times \mathbf{b}\) and verify that it is orthogonal to both a and b. \(\mathbf{a} = t\mathbf{i} + \cos t\mathbf{j} + \sin t\mathbf{k}, \mathbf{b} = \mathbf{i} - \sin t\mathbf{j} + \cos t\mathbf{k}\)
Exercise 7
Find the cross product \(\mathbf{a} \times \mathbf{b}\) and verify that it is orthogonal to both a and b. \(\mathbf{a} = \langle t, 1, 1/t \rangle, \mathbf{b} = \langle t^2, t^2, 1 \rangle\)
Exercise 8
If \(\mathbf{a} = \mathbf{i} - 2\mathbf{k}\) and \(\mathbf{b} = \mathbf{j} + \mathbf{k}\), find \(\mathbf{a} \times \mathbf{b}\). Sketch a, b, and \(\mathbf{a} \times \mathbf{b}\) as vectors starting at the origin.
Exercise 9
Find the vector, not with determinants, but by using properties of cross products. \((\mathbf{i} \times \mathbf{j}) \times \mathbf{k}\)
Exercise 10
Find the vector, not with determinants, but by using properties of cross products. \(\mathbf{k} \times (\mathbf{i} - 2\mathbf{j})\)
Exercise 11
Find the vector, not with determinants, but by using properties of cross products. \((\mathbf{j} - \mathbf{k}) \times (\mathbf{k} - \mathbf{i})\)
Exercise 12
Find the vector, not with determinants, but by using properties of cross products. \((\mathbf{i} + \mathbf{j}) \times (\mathbf{i} - \mathbf{j})\)
Exercise 13
State whether each expression is meaningful. If not, explain why. If so, state whether it is a vector or a scalar. (a) \(\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})\) (b) \(\mathbf{a} \times (\mathbf{b} \cdot \mathbf{c})\) (c) \(\mathbf{a} \times (\mathbf{b} \times \mathbf{c})\) (d) \(\mathbf{a} \cdot (\mathbf{b} \cdot \mathbf{c})\) (e) \((\mathbf{a} \cdot \mathbf{b}) \times (\mathbf{c} \cdot \mathbf{d})\) (f) \((\mathbf{a} \times \mathbf{b}) \cdot (\mathbf{c} \times \mathbf{d})\)
Exercise 14
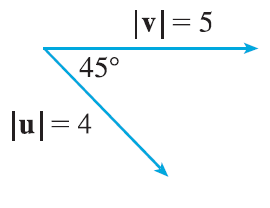
Find \(|\mathbf{u} \times \mathbf{v}|\) and determine whether \(\mathbf{u} \times \mathbf{v}\) is directed into the page or out of the page.
Exercise 15
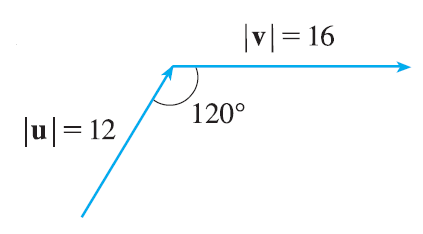
Find \(|\mathbf{u} \times \mathbf{v}|\) and determine whether \(\mathbf{u} \times \mathbf{v}\) is directed into the page or out of the page. \(|\mathbf{v}|=16, |\mathbf{u}|=12, \theta=120^\circ\)
Exercise 16
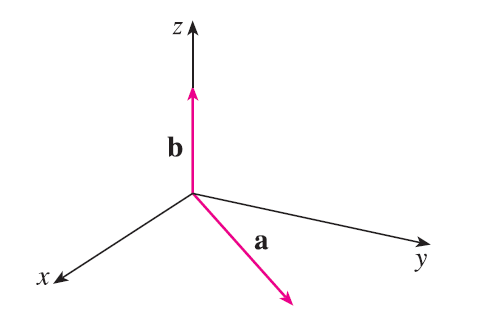
The figure shows a vector a in the xy-plane and a vector b in the direction of k. Their lengths are \(|\mathbf{a}| = 3\) and \(|\mathbf{b}| = 2\). (a) Find \(|\mathbf{a} \times \mathbf{b}|\). (b) Use the right-hand rule to decide whether the components of \(\mathbf{a} \times \mathbf{b}\) are positive, negative, or 0.
Exercise 17
If \(\mathbf{a} = \langle 2, -1, 3 \rangle\) and \(\mathbf{b} = \langle 4, 2, 1 \rangle\), find \(\mathbf{a} \times \mathbf{b}\) and \(\mathbf{b} \times \mathbf{a}\).
Exercise 18
If \(\mathbf{a} = \langle 1, 0, 1 \rangle, \mathbf{b} = \langle 2, 1, -1 \rangle\), and \(\mathbf{c} = \langle 0, 1, 3 \rangle\), show that \(\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) \ne (\mathbf{a} \times \mathbf{b}) \times \mathbf{c}\).
Exercise 19
Find two unit vectors orthogonal to both \(\langle 3, 2, 1 \rangle\) and \(\langle -1, 1, 0 \rangle\).
Exercise 20
Find two unit vectors orthogonal to both \(\mathbf{j} - \mathbf{k}\) and \(\mathbf{i} + \mathbf{j}\).
Exercise 21
Show that \(\mathbf{0} \times \mathbf{a} = \mathbf{0} = \mathbf{a} \times \mathbf{0}\) for any vector a in \(V_3\).
Exercise 22
Show that \((\mathbf{a} \times \mathbf{b}) \cdot \mathbf{b} = 0\) for all vectors a and b in \(V_3\).
Exercise 23
Prove Property 1 of cross products (Theorem 11): \(\mathbf{a} \times \mathbf{b} = -\mathbf{b} \times \mathbf{a}\).
Exercise 24
Prove Property 2 of cross products (Theorem 11): \((c\mathbf{a}) \times \mathbf{b} = c(\mathbf{a} \times \mathbf{b}) = \mathbf{a} \times (c\mathbf{b})\).
Exercise 25
Prove Property 3 of cross products (Theorem 11): \(\mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c}\).
Exercise 26
Prove Property 4 of cross products (Theorem 11): \((\mathbf{a} + \mathbf{b}) \times \mathbf{c} = \mathbf{a} \times \mathbf{c} + \mathbf{b} \times \mathbf{c}\).
Exercise 27
Find the area of the parallelogram with vertices A(-3, 0), B(-1, 3), C(5, 2), and D(3, -1).
Exercise 28
Find the area of the parallelogram with vertices P(1, 0, 2), Q(3, 3, 3), R(7, 5, 8), and S(5, 2, 7).
Exercise 29
- Find a nonzero vector orthogonal to the plane through the points P, Q, and R, and (b) find the area of triangle PQR. \(P(1, 0, 1), Q(-2, 1, 3), R(4, 2, 5)\)
Exercise 30
- Find a nonzero vector orthogonal to the plane through the points P, Q, and R, and (b) find the area of triangle PQR. \(P(0, 0, -3), Q(4, 2, 0), R(3, 3, 1)\)
Exercise 31
- Find a nonzero vector orthogonal to the plane through the points P, Q, and R, and (b) find the area of triangle PQR. \(P(0, -2, 0), Q(4, 1, -2), R(5, 3, 1)\)
Exercise 32
- Find a nonzero vector orthogonal to the plane through the points P, Q, and R, and (b) find the area of triangle PQR. \(P(2, -3, 4), Q(-1, -2, 2), R(3, 1, -3)\)
Exercise 33
Find the volume of the parallelepiped determined by the vectors a, b, and c. \(\mathbf{a} = \langle 1, 2, 3 \rangle, \mathbf{b} = \langle -1, 1, 2 \rangle, \mathbf{c} = \langle 2, 1, 4 \rangle\)
Exercise 34
Find the volume of the parallelepiped determined by the vectors a, b, and c. \(\mathbf{a} = \mathbf{i} + \mathbf{j}, \mathbf{b} = \mathbf{j} + \mathbf{k}, \mathbf{c} = \mathbf{i} + \mathbf{j} + \mathbf{k}\)
Exercise 35
Find the volume of the parallelepiped with adjacent edges PQ, PR, and PS. \(P(-2, 1, 0), Q(2, 3, 2), R(1, 4, -1), S(3, 6, 1)\)
Exercise 36
Find the volume of the parallelepiped with adjacent edges PQ, PR, and PS. \(P(3, 0, 1), Q(-1, 2, 5), R(5, 1, -1), S(0, 4, 2)\)
Exercise 37
Use the scalar triple product to verify that the vectors \(\mathbf{u} = \mathbf{i} + 5\mathbf{j} - 2\mathbf{k}, \mathbf{v} = 3\mathbf{i} - \mathbf{j},\) and \(\mathbf{w} = 5\mathbf{i} + 9\mathbf{j} - 4\mathbf{k}\) are coplanar.
Exercise 38
Use the scalar triple product to determine whether the points A(1, 3, 2), B(3, -1, 6), C(5, 2, 0), and D(3, 6, -4) lie in the same plane.
Exercise 39
A bicycle pedal is pushed by a foot with a 60-N force as shown. The shaft of the pedal is 18 cm long. Find the magnitude of the torque about P.
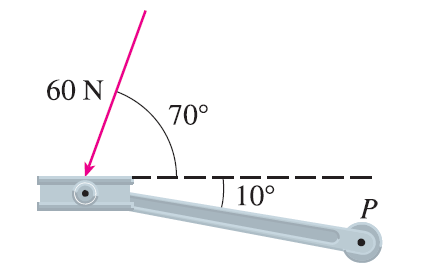
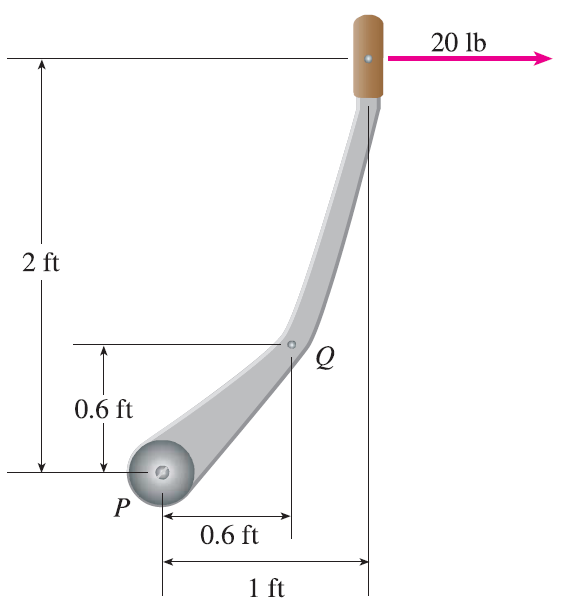
Exercise 40
- A horizontal force of 20 lb is applied to the handle of a gearshift lever as shown. Find the magnitude of the torque about the pivot point P.
- Find the magnitude of the torque about P if the same force is applied at the elbow Q of the lever.
Exercise 41
A wrench 30 cm long lies along the positive y-axis and grips a bolt at the origin. A force is applied in the direction \(\langle 0, 3, -4 \rangle\) at the end of the wrench. Find the magnitude of the force needed to supply 100 N·m of torque to the bolt.
Exercise 42
Let \(\mathbf{v} = 5\mathbf{j}\) and let u be a vector with length 3 that starts at the origin and rotates in the xy-plane. Find the maximum and minimum values of the length of the vector \(\mathbf{u} \times \mathbf{v}\). In what direction does \(\mathbf{u} \times \mathbf{v}\) point?
Exercise 43
If \(\mathbf{a} \cdot \mathbf{b} = \sqrt{3}\) and \(\mathbf{a} \times \mathbf{b} = \langle 1, 2, 2 \rangle\), find the angle between a and b.
Exercise 44
- Find all vectors v such that \(\langle 1, 2, 1 \rangle \times \mathbf{v} = \langle 3, 1, -5 \rangle\).
- Explain why there is no vector v such that \(\langle 1, 2, 1 \rangle \times \mathbf{v} = \langle 3, 1, 5 \rangle\).
Exercise 45
- Let P be a point not on the line L that passes through the points Q and R. Show that the distance \(d\) from the point P to the line L is \[ d = \frac{|\mathbf{a} \times \mathbf{b}|}{|\mathbf{a}|} \] where \(\mathbf{a} = \vec{QR}\) and \(\mathbf{b} = \vec{QP}\).
- Use the formula in part (a) to find the distance from the point P(1, 1, 1) to the line through Q(0, 6, 8) and R(-1, 4, 7).
Exercise 46
- Let P be a point not on the plane that passes through the points Q, R, and S. Show that the distance \(d\) from P to the plane is \[ d = \frac{|\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})|}{|\mathbf{a} \times \mathbf{b}|} \] where \(\mathbf{a} = \vec{QR}, \mathbf{b} = \vec{QS},\) and \(\mathbf{c} = \vec{QP}\).
- Use the formula in part (a) to find the distance from the point P(2, 1, 4) to the plane through the points Q(1, 0, 0), R(0, 2, 0), and S(0, 0, 3).
Exercise 47
Show that \(|\mathbf{a} \times \mathbf{b}|^2 = |\mathbf{a}|^2|\mathbf{b}|^2 - (\mathbf{a} \cdot \mathbf{b})^2\).
Exercise 48
If \(\mathbf{a} + \mathbf{b} + \mathbf{c} = \mathbf{0}\), show that \(\mathbf{a} \times \mathbf{b} = \mathbf{b} \times \mathbf{c} = \mathbf{c} \times \mathbf{a}\).
Exercise 49
Prove that \((\mathbf{a} - \mathbf{b}) \times (\mathbf{a} + \mathbf{b}) = 2(\mathbf{a} \times \mathbf{b})\).
Exercise 50
Prove Property 6 of cross products, that is, \(\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) = (\mathbf{a} \cdot \mathbf{c})\mathbf{b} - (\mathbf{a} \cdot \mathbf{b})\mathbf{c}\).
Exercise 51
Use Exercise 50 to prove that \(\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) + \mathbf{b} \times (\mathbf{c} \times \mathbf{a}) + \mathbf{c} \times (\mathbf{a} \times \mathbf{b}) = \mathbf{0}\).
Exercise 52
Prove that \[ (\mathbf{a} \times \mathbf{b}) \cdot (\mathbf{c} \times \mathbf{d}) = \begin{vmatrix} \mathbf{a} \cdot \mathbf{c} & \mathbf{b} \cdot \mathbf{c} \\ \mathbf{a} \cdot \mathbf{d} & \mathbf{b} \cdot \mathbf{d} \end{vmatrix} \]
Exercise 53
Suppose that \(\mathbf{a} \ne \mathbf{0}\). (a) If \(\mathbf{a} \cdot \mathbf{b} = \mathbf{a} \cdot \mathbf{c}\), does it follow that \(\mathbf{b} = \mathbf{c}\)? (b) If \(\mathbf{a} \times \mathbf{b} = \mathbf{a} \times \mathbf{c}\), does it follow that \(\mathbf{b} = \mathbf{c}\)? (c) If \(\mathbf{a} \cdot \mathbf{b} = \mathbf{a} \cdot \mathbf{c}\) and \(\mathbf{a} \times \mathbf{b} = \mathbf{a} \times \mathbf{c}\), does it follow that \(\mathbf{b} = \mathbf{c}\)?
Exercise 54
If \(\mathbf{v}_1, \mathbf{v}_2,\) and \(\mathbf{v}_3\) are noncoplanar vectors, let \[ \mathbf{k}_1 = \frac{\mathbf{v}_2 \times \mathbf{v}_3}{\mathbf{v}_1 \cdot (\mathbf{v}_2 \times \mathbf{v}_3)} \quad \mathbf{k}_2 = \frac{\mathbf{v}_3 \times \mathbf{v}_1}{\mathbf{v}_1 \cdot (\mathbf{v}_2 \times \mathbf{v}_3)} \quad \mathbf{k}_3 = \frac{\mathbf{v}_1 \times \mathbf{v}_2}{\mathbf{v}_1 \cdot (\mathbf{v}_2 \times \mathbf{v}_3)} \] (These vectors occur in the study of crystallography. Vectors of the form \(n_1\mathbf{v}_1 + n_2\mathbf{v}_2 + n_3\mathbf{v}_3\), where each \(n_i\) is an integer, form a lattice for a crystal. Vectors written similarly in terms of \(\mathbf{k}_1, \mathbf{k}_2,\) and \(\mathbf{k}_3\) form the reciprocal lattice.) (a) Show that \(\mathbf{k}_i\) is perpendicular to \(\mathbf{v}_j\) if \(i \ne j\). (b) Show that \(\mathbf{k}_i \cdot \mathbf{v}_i = 1\) for \(i = 1, 2, 3\). (c) Show that \(\mathbf{k}_1 \cdot (\mathbf{k}_2 \times \mathbf{k}_3) = \frac{1}{\mathbf{v}_1 \cdot (\mathbf{v}_2 \times \mathbf{v}_3)}\).