Section 12.5: Lines & Planes
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 12.5: Lines & Planes |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 3:57 AM |
Table of contents
- Lines
- Line Segment
- What are skew lines?
- Planes
- Example Problems
- When are planes called parallel? If they are not parallel, What is the angle between two non-parallel planes?
- Distance between a point and a plane
- Distance between two skew lines
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
- Exercise 49
- Exercise 50
- Exercise 51
- Exercise 52
- Exercise 53
- Exercise 54
- Exercise 55
- Exercise 56
- Exercise 57
- Exercise 58
- Exercise 59
- Exercise 60
- Exercise 61
- Exercise 62
- Exercise 63
- Exercise 64
- Exercise 65
- Exercise 66
- Exercise 67
- Exercise 68
- Exercise 69
- Exercise 70
- Exercise 71
- Exercise 72
- Exercise 73
- Exercise 74
- Exercise 75
- Exercise 76
- Exercise 77
- Exercise 78
- Exercise 79
- Exercise 80
- Exercise 81
- Exercise 82
- Exercise 83
Lines
A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given. The equation of the line can then be written using the point-slope form.
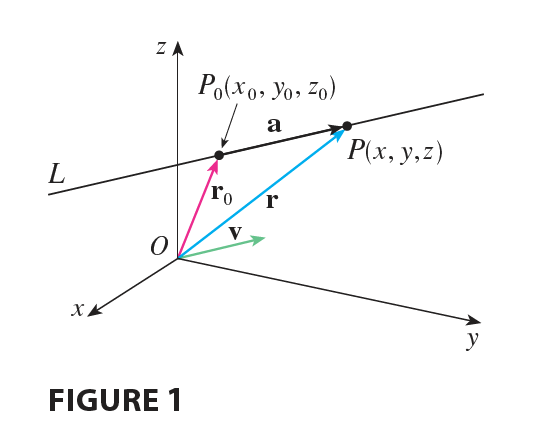
Likewise, a line L in three-dimensional space is determined when we know a point \(P_0(x_0, y_0, z_0)\) on L and the direction of L. In three dimensions the direction of a line is conveniently described by a vector, so we let v be a vector parallel to L. Let \(P(x, y, z)\) be an arbitrary point on L and let \(\mathbf{r}_0\) and r be the position vectors of \(P_0\) and \(P\) (that is, they have representations \(\vec{OP_0}\) and \(\vec{OP}\)). If a is the vector with representation \(\vec{P_0P}\), as in Figure 1, then the Triangle Law for vector addition gives \(\mathbf{r} = \mathbf{r}_0 + \mathbf{a}\). But, since a and v are parallel vectors, there is a scalar \(t\) such that \(\mathbf{a} = t\mathbf{v}\). Thus \[ \mathbf{r} = \mathbf{r}_0 + t\mathbf{v} \tag{1} \] which is a vector equation of L. Each value of the parameter \(t\) gives the position vector r of a point on L. In other words, as \(t\) varies, the line is traced out by the tip of the vector r. As Figure 2 indicates, positive values of \(t\) correspond to points on L that lie on one side of \(P_0\), whereas negative values of \(t\) correspond to points that lie on the other side of \(P_0\).
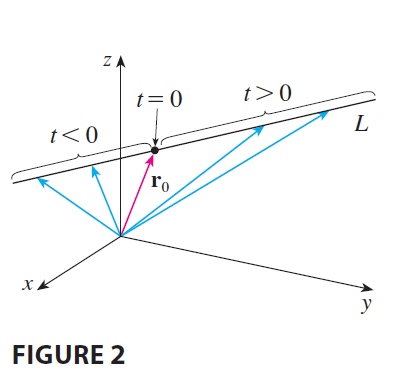
If the vector v that gives the direction of the line L is written in component form as \(\mathbf{v} = \langle a, b, c \rangle\), then we have \(t\mathbf{v} = \langle ta, tb, tc \rangle\). We can also write \(\mathbf{r} = \langle x, y, z \rangle\) and \(\mathbf{r}_0 = \langle x_0, y_0, z_0 \rangle\), so the vector equation (1) becomes \[ \langle x, y, z \rangle = \langle x_0 + ta, y_0 + tb, z_0 + tc \rangle \] Two vectors are equal if and only if corresponding components are equal. Therefore we have the three scalar equations: \[ x = x_0 + at \quad y = y_0 + bt \quad z = z_0 + ct \] where \(t \in \mathbb{R}\). These equations are called parametric equations of the line L through the point \(P_0(x_0, y_0, z_0)\) and parallel to the vector \(\mathbf{v} = \langle a, b, c \rangle\). Each value of the parameter \(t\) gives a point \((x, y, z)\) on L.
Parametric equations for a line through the point \((x_0, y_0, z_0)\) and parallel to the direction vector \(\langle a, b, c \rangle\) are \[ x = x_0 + at \quad y = y_0 + bt \quad z = z_0 + ct \tag{2} \]
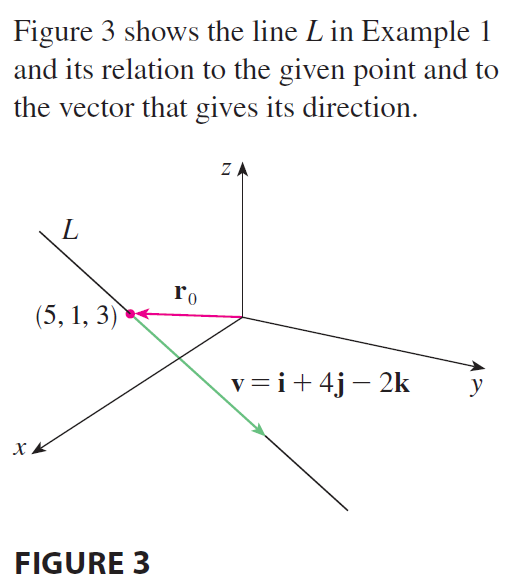
EXAMPLE 1 (a) Find a vector equation and parametric equations for the line that passes through the point \((5, 1, 3)\) and is parallel to the vector \(\mathbf{i} + 4\mathbf{j} - 2\mathbf{k}\). (b) Find two other points on the line.
The vector equation and parametric equations of a line are not unique. If we change the point or the parameter or choose a different parallel vector, then the equations change. For instance, if, instead of \((5, 1, 3)\), we choose the point \((6, 5, 1)\) in Example 1, then the parametric equations of the line become \[ x = 6 + t \quad y = 5 + 4t \quad z = 1 - 2t \] Or, if we stay with the point \((5, 1, 3)\) but choose the parallel vector \(2\mathbf{i} + 8\mathbf{j} - 4\mathbf{k}\), we arrive at the equations \[ x = 5 + 2t \quad y = 1 + 8t \quad z = 3 - 4t \] In general, if a vector \(\mathbf{v} = \langle a, b, c \rangle\) is used to describe the direction of a line L, then the numbers \(a, b,\) and \(c\) are called direction numbers of L. Since any vector parallel to v could also be used, we see that any three numbers proportional to \(a, b,\) and \(c\) could also be used as a set of direction numbers for L.
Another way of describing a line L is to eliminate the parameter \(t\) from Equations 2. If none of \(a, b,\) or \(c\) is 0, we can solve each of these equations for \(t\): \[ t = \frac{x - x_0}{a} \quad t = \frac{y - y_0}{b} \quad t = \frac{z - z_0}{c} \] Equating the results, we obtain \[ \frac{x - x_0}{a} = \frac{y - y_0}{b} = \frac{z - z_0}{c} \tag{3} \] These equations are called symmetric equations of L. Notice that the numbers \(a, b,\) and \(c\) that appear in the denominators of Equations 3 are direction numbers of L, that is, components of a vector parallel to L. If one of \(a, b,\) or \(c\) is 0, we can still eliminate \(t\). For instance, if \(a = 0\), we could write the equations of L as \[ x = x_0 \quad \frac{y - y_0}{b} = \frac{z - z_0}{c} \] This means that L lies in the vertical plane \(x = x_0\).
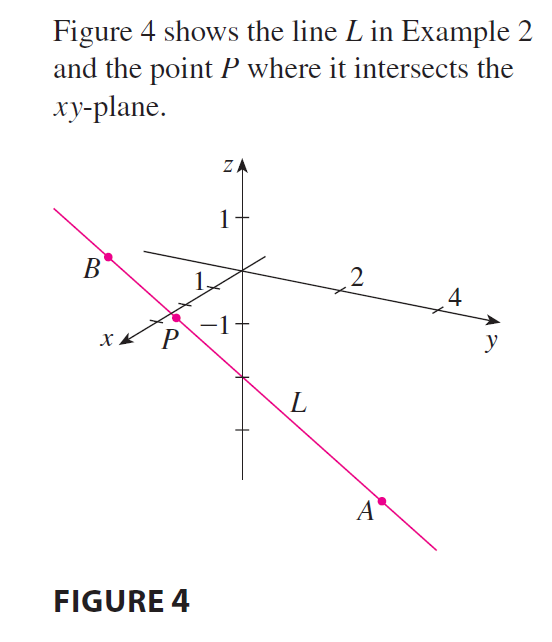
EXAMPLE 2 (a) Find parametric equations and symmetric equations of the line that passes through the points \(A(2, 4, -3)\) and \(B(3, -1, 1)\). (b) At what point does this line intersect the xy-plane?
Line Segment
Often, we need a description, not of an entire line, but of just a line segment. How, for instance, could we describe the line segment AB in Example 2? If we put \(t = 0\) in the parametric equations in Example 2(a), we get the point \((2, 4, -3)\) and if we put \(t = 1\) we get \((3, -1, 1)\). So the line segment AB is described by the parametric equations \[ x = 2 + t \quad y = 4 - 5t \quad z = -3 + 4t \quad 0 \le t \le 1 \] or by the corresponding vector equation \[ \mathbf{r}(t) = \langle 2 + t, 4 - 5t, -3 + 4t \rangle \quad 0 \le t \le 1 \] In general, we know from Equation 1 that the vector equation of a line through the (tip of the) vector \(\mathbf{r}_0\) in the direction of a vector v is \(\mathbf{r} = \mathbf{r}_0 + t\mathbf{v}\). If the line also passes through (the tip of) \(\mathbf{r}_1\), then we can take \(\mathbf{v} = \mathbf{r}_1 - \mathbf{r}_0\) and so its vector equation is \[ \mathbf{r} = \mathbf{r}_0 + t(\mathbf{r}_1 - \mathbf{r}_0) = (1 - t)\mathbf{r}_0 + t\mathbf{r}_1 \] The line segment from \(\mathbf{r}_0\) to \(\mathbf{r}_1\) is given by the parameter interval \(0 \le t \le 1\).
The line segment from \(\mathbf{r}_0\) to \(\mathbf{r}_1\) is given by the vector equation \[ \mathbf{r}(t) = (1 - t)\mathbf{r}_0 + t\mathbf{r}_1 \quad 0 \le t \le 1 \tag{4} \]
What are skew lines?
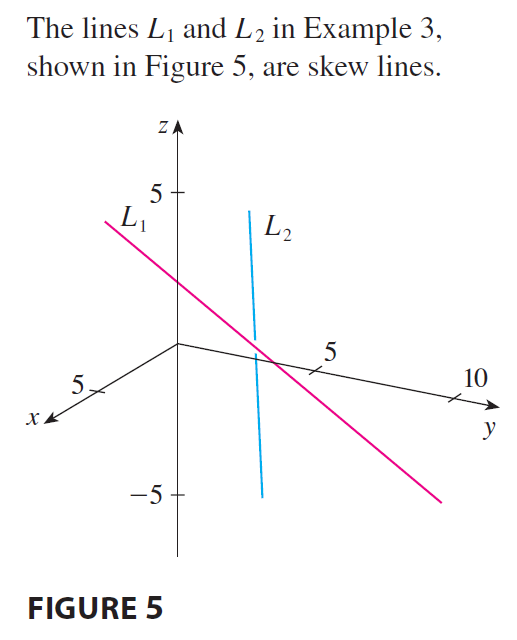
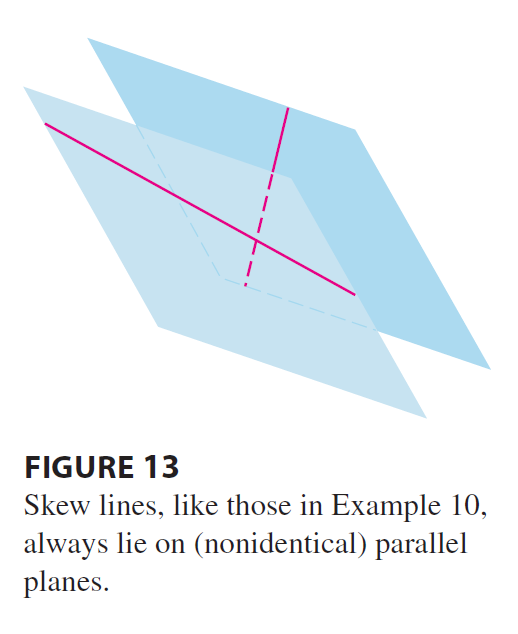
EXAMPLE 3 Show that the lines \(L_1\) and \(L_2\) with parametric equations \[ L_1: x = 1 + t \quad y = -2 + 3t \quad z = 4 - t \] \[ L_2: x = 2s \quad y = 3 + s \quad z = -3 + 4s \] are skew lines; that is, they do not intersect and are not parallel (and therefore do not lie in the same plane).
Planes
Although a line in space is determined by a point and a direction, a plane in space is more difficult to describe. A single vector parallel to a plane is not enough to convey the “direction” of the plane, but a vector perpendicular to the plane does completely specify its direction. Thus a plane in space is determined by a point \(P_0(x_0, y_0, z_0)\) in the plane and a vector n that is orthogonal to the plane. This orthogonal vector n is called a normal vector.
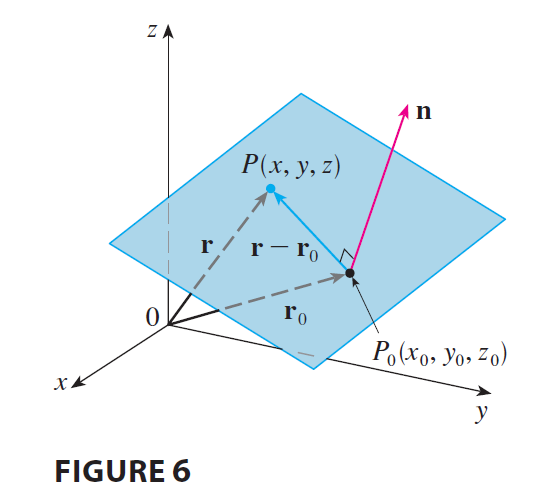
Let \(P(x, y, z)\) be an arbitrary point in the plane, and let \(\mathbf{r}_0\) and r be the position vectors of \(P_0\) and \(P\). Then the vector \(\mathbf{r} - \mathbf{r}_0\) is represented by \(\vec{P_0P}\). The normal vector n is orthogonal to every vector in the given plane. In particular, n is orthogonal to \(\mathbf{r} - \mathbf{r}_0\) and so we have \[ \mathbf{n} \cdot (\mathbf{r} - \mathbf{r}_0) = 0 \tag{5} \] which can be rewritten as \[ \mathbf{n} \cdot \mathbf{r} = \mathbf{n} \cdot \mathbf{r}_0 \tag{6} \] Either Equation 5 or Equation 6 is called a vector equation of the plane.
To obtain a scalar equation for the plane, we write \(\mathbf{n} = \langle a, b, c \rangle, \mathbf{r} = \langle x, y, z \rangle,\) and \(\mathbf{r}_0 = \langle x_0, y_0, z_0 \rangle\). Then the vector equation (5) becomes \[ \langle a, b, c \rangle \cdot \langle x - x_0, y - y_0, z - z_0 \rangle = 0 \] or \[ a(x - x_0) + b(y - y_0) + c(z - z_0) = 0 \]
A scalar equation of the plane through point \(P_0(x_0, y_0, z_0)\) with normal vector \(\mathbf{n} = \langle a, b, c \rangle\) is \[ a(x - x_0) + b(y - y_0) + c(z - z_0) = 0 \tag{7} \]
EXAMPLE 4 Find an equation of the plane through the point \((2, 4, -1)\) with normal vector \(\mathbf{n} = \langle 2, 3, 4 \rangle\). Find the intercepts and sketch the plane.
By collecting terms in Equation 7 as we did in Example 4, we can rewrite the equation of a plane as \[ ax + by + cz + d = 0 \tag{8} \] where \(d = -(ax_0 + by_0 + cz_0)\). Equation 8 is called a linear equation in \(x, y,\) and \(z\). Conversely, it can be shown that if \(a, b,\) and \(c\) are not all 0, then the linear equation (8) represents a plane with normal vector \(\langle a, b, c \rangle\).
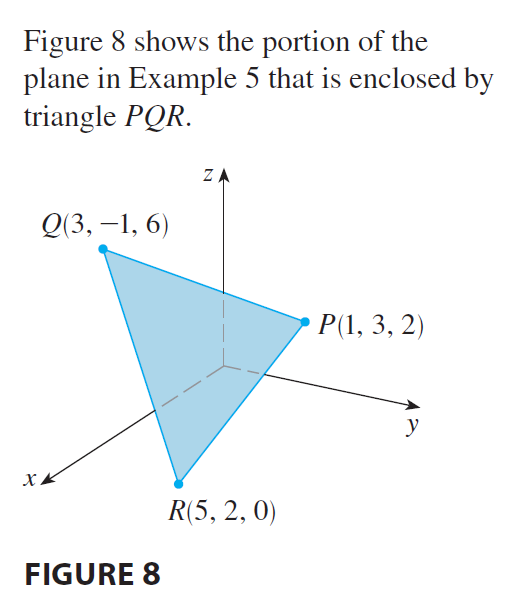
EXAMPLE 5 Find an equation of the plane that passes through the points \(P(1, 3, 2), Q(3, -1, 6),\) and \(R(5, 2, 0)\).
Example Problems
EXAMPLE 6 Find the point at which the line with parametric equations \(x = 2 + 3t, y = -4t, z = 5 + t\) intersects the plane \(4x + 5y - 2z = 18\).
When are planes called parallel? If they are not parallel, What is the angle between two non-parallel planes?
Two planes are parallel if their normal vectors are parallel. For instance, the planes \(x + 2y - 3z = 4\) and \(2x + 4y - 6z = 3\) are parallel because their normal vectors are \(\mathbf{n}_1 = \langle 1, 2, -3 \rangle\) and \(\mathbf{n}_2 = \langle 2, 4, -6 \rangle\) and \(\mathbf{n}_2 = 2\mathbf{n}_1\). If two planes are not parallel, then they intersect in a straight line and the angle between the two planes is defined as the acute angle between their normal vectors (see angle \(\theta\) in Figure 9).
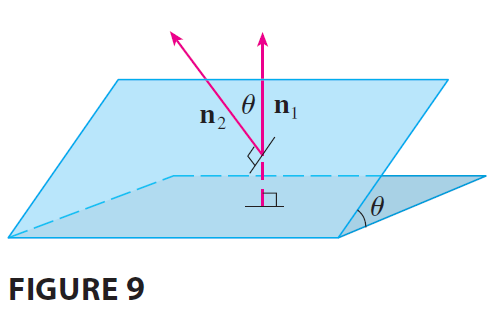
EXAMPLE 7 (a) Find the angle between the planes \(x + y + z = 1\) and \(x - 2y + 3z = 1\). (b) Find symmetric equations for the line of intersection L of these two planes.
Distance between a point and a plane
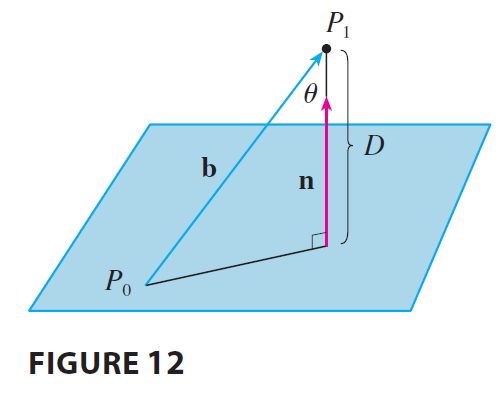
EXAMPLE 8 Find a formula for the distance \(D\) from a point \(P_1(x_1, y_1, z_1)\) to the plane \(ax + by + cz + d = 0\).
EXAMPLE 9 Find the distance between the parallel planes \(10x + 2y - 2z = 5\) and \(5x + y - z = 1\).
Distance between two skew lines
EXAMPLE 10 In Example 3 we showed that the lines \[ L_1: x = 1 + t \quad y = -2 + 3t \quad z = 4 - t \] \[ L_2: x = 2s \quad y = 3 + s \quad z = -3 + 4s \] are skew. Find the distance between them.
Exercise 1
Determine whether each statement is true or false in \(\mathbb{R}^3\). (a) Two lines parallel to a
third line are parallel. (b) Two lines perpendicular to a third line are
parallel. (c) Two planes parallel to a third plane are parallel. (d) Two
planes perpendicular to a third plane are parallel. (e) Two lines
parallel to a plane are parallel. (f) Two lines perpendicular to a plane
are parallel. (g) Two planes parallel to a line are parallel. Two
planes perpendicular to a line are parallel. (i) Two planes either
intersect or are parallel. (j) Two lines either intersect or are
parallel. (k) A plane and a line either intersect or are parallel.
Exercise 2
Find a vector equation and parametric equations for the line through the point \((6, -5, 2)\) and parallel to the vector \(\langle 1, 3, -\frac{2}{3} \rangle\).
Exercise 3
Find a vector equation and parametric equations for the line through the point \((2, 2.4, 3.5)\) and parallel to the vector \(3\mathbf{i} + 2\mathbf{j} - \mathbf{k}\).
Exercise 4
Find a vector equation and parametric equations for the line through the point \((0, 14, -10)\) and parallel to the line \(x = -1 + 2t, y = 6 - 3t, z = 3 + 9t\).
Exercise 5
Find a vector equation and parametric equations for the line through the point \((1, 0, 6)\) and perpendicular to the plane \(x + 3y + z = 5\).
Exercise 6
Find parametric equations and symmetric equations for the line through the origin and the point \((4, 3, -1)\).
Exercise 7
Find parametric equations and symmetric equations for the line through the points \((0, \frac{1}{2}, 1)\) and \((2, 1, -3)\).
Exercise 8
Find parametric equations and symmetric equations for the line through the points \((1, 2.4, 4.6)\) and \((2.6, 1.2, 0.3)\).
Exercise 9
Find parametric equations and symmetric equations for the line through the points \((-8, 1, 4)\) and \((3, -2, 4)\).
Exercise 10
Find parametric equations and symmetric equations for the line through \((2, 1, 0)\) and perpendicular to both \(\mathbf{i} + \mathbf{j}\) and \(\mathbf{j} + \mathbf{k}\).
Exercise 11
Find parametric equations and symmetric equations for the line through \((-6, 2, 3)\) and parallel to the line \(\frac{x}{2} = \frac{y}{3} = z + 1\).
Exercise 12
Find parametric equations and symmetric equations for the line of intersection of the planes \(x + 2y + 3z = 1\) and \(x - y + z = 1\).
Exercise 13
Is the line through \((-4, -6, 1)\) and \((-2, 0, -3)\) parallel to the line through \((10, 18, 4)\) and \((5, 3, 14)\)?
Exercise 14
Is the line through \((-2, 4, 0)\) and \((1, 1, 1)\) perpendicular to the line through \((2, 3, 4)\) and \((3, -1, -8)\)?
Exercise 15
- Find symmetric equations for the line that passes through the point \((1, -5, 6)\) and is parallel to the vector \(\langle -1, 2, -3 \rangle\).
- Find the points in which the required line in part (a) intersects the coordinate planes.
Exercise 16
- Find parametric equations for the line through \((2, 4, 6)\) that is perpendicular to the plane \(x - y + 3z = 7\).
- In what points does this line intersect the coordinate planes?
Exercise 17
Find a vector equation for the line segment from \((6, -1, 9)\) to \((7, 6, 0)\).
Exercise 18
Find parametric equations for the line segment from \((-2, 18, 31)\) to \((11, -4, 48)\).
Exercise 19
Determine whether the lines \(L_1\) and \(L_2\) are parallel, skew, or intersecting. If they intersect, find the point of intersection. \(L_1: x = -3 + 2t, y = 4 - t, z = 1 + 3t\) \(L_2: x = 1 + 4s, y = 3 - 2s, z = 4 + 5s\)
Exercise 20
Determine whether the lines \(L_1\) and \(L_2\) are parallel, skew, or intersecting. If they intersect, find the point of intersection. \(L_1: x = 5 - 12t, y = 3 + 9t, z = 1 - 3t\) \(L_2: x = 3 + 8s, y = -6s, z = 7 + 2s\)
Exercise 21
Determine whether the lines \(L_1\) and \(L_2\) are parallel, skew, or intersecting. If they intersect, find the point of intersection. \(L_1: \frac{x-2}{1} = \frac{y-3}{-2} = \frac{z-1}{-3}\) \(L_2: \frac{x-3}{1} = \frac{y+4}{3} = \frac{z-2}{-7}\)
Exercise 22
Determine whether the lines \(L_1\) and \(L_2\) are parallel, skew, or intersecting. If they intersect, find the point of intersection. \(L_1: \frac{x}{1} = \frac{y-1}{-1} = \frac{z-2}{3}\) \(L_2: \frac{x-2}{2} = \frac{y-3}{-2} = \frac{z}{7}\)
Exercise 23
Find an equation of the plane through the origin and perpendicular to the vector \(\langle 1, -2, 5 \rangle\).
Exercise 24
Find an equation of the plane through the point \((5, 3, 5)\) and with normal vector \(2\mathbf{i} + \mathbf{j} - \mathbf{k}\).
Exercise 25
Find an equation of the plane through the point \((-1, \frac{1}{2}, 3)\) and with normal vector \(\mathbf{i} + 4\mathbf{j} + \mathbf{k}\).
Exercise 26
Find an equation of the plane through the point \((2, 0, 1)\) and perpendicular to the line \(x = 3t, y = 2 - t, z = 3 + 4t\).
Exercise 27
Find an equation of the plane through the point \((1, -1, -1)\) and parallel to the plane \(5x - y - z = 6\).
Exercise 28
Find an equation of the plane through the point \((3, -2, 8)\) and parallel to the plane \(z = x + y\).
Exercise 29
Find an equation of the plane through the point \((1, \frac{1}{2}, \frac{1}{3})\) and parallel to the plane \(x + y + z = 0\).
Exercise 30
Find an equation of the plane that contains the line \(x = 1 + t, y = 2 - t, z = 4 - 3t\) and is parallel to the plane \(5x + 2y + z = 1\).
Exercise 31
Find an equation of the plane through the points \((0, 1, 1), (1, 0, 1),\) and \((1, 1, 0)\).
Exercise 32
Find an equation of the plane through the origin and the points \((3, -2, 1)\) and \((1, 1, 1)\).
Exercise 33
Find an equation of the plane through the points \((2, 1, 2), (3, -8, 6),\) and \((-2, -3, 1)\).
Exercise 34
Find an equation of the plane through the points \((3, 0, -1), (-2, -2, 3),\) and \((7, 1, -4)\).
Exercise 35
Find an equation of the plane that passes through the point \((3, 5, -1)\) and contains the line \(x = 4 - t, y = 2t - 1, z = -3t\).
Exercise 36
Find an equation of the plane that passes through the point \((6, -1, 3)\) and contains the line with symmetric equations \(\frac{x}{3} = y + 4 = \frac{z}{2}\).
Exercise 37
Find an equation of the plane that passes through the point \((3, 1, 4)\) and contains the line of intersection of the planes \(x + 2y + 3z = 1\) and \(2x - y + z = -3\).
Exercise 38
Find an equation of the plane that passes through the points \((0, -2, 5)\) and \((-1, 3, 1)\) and is perpendicular to the plane \(2z = 5x + 4y\).
Exercise 39
Find an equation of the plane that passes through the point \((1, 5, 1)\) and is perpendicular to the planes \(2x + y - 2z = 2\) and \(x + 3z = 4\).
Exercise 40
Find an equation of the plane that passes through the line of intersection of the planes \(x - z = 1\) and \(y + 2z = 3\) and is perpendicular to the plane \(x + y - 2z = 1\).
Exercise 41
Use intercepts to help sketch the plane \(2x + 5y + z = 10\).
Exercise 42
Use intercepts to help sketch the plane \(3x + y + 2z = 6\).
Exercise 43
Use intercepts to help sketch the plane \(6x - 3y + 4z = 6\).
Exercise 44
Use intercepts to help sketch the plane \(6x + 5y - 3z = 15\).
Exercise 45
Find the point at which the line intersects the given plane. \(x = 2 - 2t, y = 3t, z = 1 + t; \quad x + 2y - z = 7\)
Exercise 46
Find the point at which the line intersects the given plane. \(x = t - 1, y = 1 + 2t, z = 3 - t; \quad 3x - y + 2z = 5\)
Exercise 47
Find the point at which the line intersects the given plane. \(5x = y/2 = z + 2; \quad 10x - 7y + 3z + 24 = 0\)
Exercise 48
Where does the line through \((-3, 1, 0)\) and \((-1, 5, 6)\) intersect the plane \(2x + y - z = -2\)?
Exercise 49
Find direction numbers for the line of intersection of the planes \(x + y + z = 1\) and \(x + z = 0\).
Exercise 50
Find the cosine of the angle between the planes \(x + y + z = 0\) and \(x + 2y + 3z = 1\).
Exercise 51
Determine whether the planes are parallel, perpendicular, or neither. If neither, find the angle between them. (Round to one decimal place.) \(x + 4y - 3z = 1, \quad -3x + 6y + 7z = 0\)
Exercise 52
Determine whether the planes are parallel, perpendicular, or neither. If neither, find the angle between them. (Round to one decimal place.) \(9x - 3y + 6z = 2, \quad 2y = 6x + 4z\)
Exercise 53
Determine whether the planes are parallel, perpendicular, or neither. If neither, find the angle between them. (Round to one decimal place.) \(x + 2y - z = 2, \quad 2x - 2y + z = 1\)
Exercise 54
Determine whether the planes are parallel, perpendicular, or neither. If neither, find the angle between them. (Round to one decimal place.) \(x - y + 3z = 1, \quad 3x + y - z = 2\)
Exercise 55
Determine whether the planes are parallel, perpendicular, or neither. If neither, find the angle between them. (Round to one decimal place.) \(2x - 3y = z, \quad 4x = 3 + 6y + 2z\)
Exercise 56
Determine whether the planes are parallel, perpendicular, or neither. If neither, find the angle between them. (Round to one decimal place.) \(5x + 2y + 3z = 2, \quad y = 4x - 6z\)
Exercise 57
- Find parametric equations for the line of intersection of the planes \(x + y + z = 1\) and \(x + 2y + 2z = 1\).
- Find the angle between the planes.
Exercise 58
- Find parametric equations for the line of intersection of the planes \(3x - 2y + z = 1\) and \(2x + y - 3z = 3\).
- Find the angle between the planes.
Exercise 59
Find symmetric equations for the line of intersection of the planes. \(5x - 2y - 2z = 1, \quad 4x + y + z = 6\)
Exercise 60
Find symmetric equations for the line of intersection of the planes. \(z = 2x - y - 5, \quad z = 4x + 3y - 5\)
Exercise 61
Find an equation for the plane consisting of all points that are equidistant from the points \((1, 0, -2)\) and \((3, 4, 0)\).
Exercise 62
Find an equation for the plane consisting of all points that are equidistant from the points \((2, 5, 5)\) and \((-6, 3, 1)\).
Exercise 63
Find an equation of the plane with x-intercept a, y-intercept b, and z-intercept c.
Exercise 64
- Find the point at which the given lines intersect: \(\mathbf{r} = \langle 1, 1, 0 \rangle + t\langle 1, -1, 2 \rangle\) \(\mathbf{r} = \langle 2, 0, 2 \rangle + s\langle -1, 1, 0 \rangle\)
- Find an equation of the plane that contains these lines.
Exercise 65
Find parametric equations for the line through the point \((0, 1, 2)\) that is parallel to the plane \(x + y + z = 2\) and perpendicular to the line \(x = 1 + t, y = 1 - t, z = 2t\).
Exercise 66
Find parametric equations for the line through the point \((0, 1, 2)\) that is perpendicular to the line \(x = 1 + t, y = 1 - t, z = 2t\) and intersects this line.
Exercise 67
Which of the following four planes are parallel? Are any of them identical? \(P_1: 3x + 6y - 3z = 6\) \(P_2: 4x - 12y + 8z = 5\) \(P_3: 9y = 1 + 3x + 6z\) \(P_4: z = x + 2y - 2\)
Exercise 68
Which of the following four lines are parallel? Are any of them identical? \(L_1: x = 1 + 6t, y = 1 - 3t, z = 12t + 5\) \(L_2: x = 1 + 2t, y = t, z = 1 + 4t\) \(L_3: 2x - 2 = 4 - 4y = z + 1\) \(L_4: \mathbf{r} = \langle 3, 1, 5 \rangle + t\langle 4, 2, 8 \rangle\)
Exercise 69
Use the formula in Exercise 12.4.45 to find the distance from the point to the given line. \((4, 1, -2); \quad x = 1 + t, y = 3 - 2t, z = 4 - 3t\)
Exercise 70
Use the formula in Exercise 12.4.45 to find the distance from the point to the given line. \((0, 1, 3); \quad x = 2t, y = 6 - 2t, z = 3 + t\)
Exercise 71
Find the distance from the point to the given plane. \((1, -2, 4), \quad 3x + 2y + 6z = 5\)
Exercise 72
Find the distance from the point to the given plane. \((-6, 3, 5), \quad x - 2y - 4z = 8\)
Exercise 73
Find the distance between the given parallel planes. \(2x - 3y + z = 4, \quad 4x - 6y + 2z = 3\)
Exercise 74
Find the distance between the given parallel planes. \(6z = 4y - 2x, \quad 9z = 1 - 3x + 6y\)
Exercise 75
Show that the distance between the parallel planes \(ax + by + cz + d_1 = 0\) and \(ax + by + cz + d_2 = 0\) is \[ D = \frac{|d_1 - d_2|}{\sqrt{a^2 + b^2 + c^2}} \]
Exercise 76
Find equations of the planes that are parallel to the plane \(x + 2y - 2z = 1\) and two units away from it.
Exercise 77
Show that the lines with symmetric equations \(x = y = z\) and \(x + 1 = y/2 = z/3\) are skew, and find the distance between these lines.
Exercise 78
Find the distance between the skew lines with parametric equations \(x = 1 + t, y = 1 + 6t, z = 2t,\) and \(x = 1 + 2s, y = 5 + 15s, z = -2 + 6s\).
Exercise 79
Let \(L_1\) be the line through the origin and the point \((2, 0, -1)\). Let \(L_2\) be the line through the points \((1, -1, 1)\) and \((4, 1, 3)\). Find the distance between \(L_1\) and \(L_2\).
Exercise 80
Let \(L_1\) be the line through the points \((1, 2, 6)\) and \((2, 4, 8)\). Let \(L_2\) be the line of intersection of the planes \(\mathcal{P}_1\) and \(\mathcal{P}_2\), where \(\mathcal{P}_1\) is the plane \(x - y + 2z + 1 = 0\) and \(\mathcal{P}_2\) is the plane through the points \((3, 2, -1), (0, 0, 1),\) and \((1, 2, 1)\). Calculate the distance between \(L_1\) and \(L_2\).
Exercise 81
Two tanks are participating in a battle simulation. Tank A is at point \((325, 810, 561)\) and tank B is positioned at point \((765, 675, 599)\). (a) Find parametric equations for the line of sight between the tanks. (b) If we divide the line of sight into 5 equal segments, the elevations of the terrain at the four intermediate points from tank A to tank B are 549, 566, 586, and 589. Can the tanks see each other?
Exercise 82
Give a geometric description of each family of planes. (a) \(x + y + z = c\) (b) \(x + y + cz = 1\) (c) \(y \cos\theta + z \sin\theta = 1\)
Exercise 83
If a, b, and c are not all 0, show that the equation \(ax + by + cz + d = 0\) represents a plane and \(\langle a, b, c \rangle\) is a normal vector to the plane. Hint: Suppose \(a \ne 0\) and rewrite the equation in the form \(a(x + d/a) + b(y - 0) + c(z - 0) = 0\)