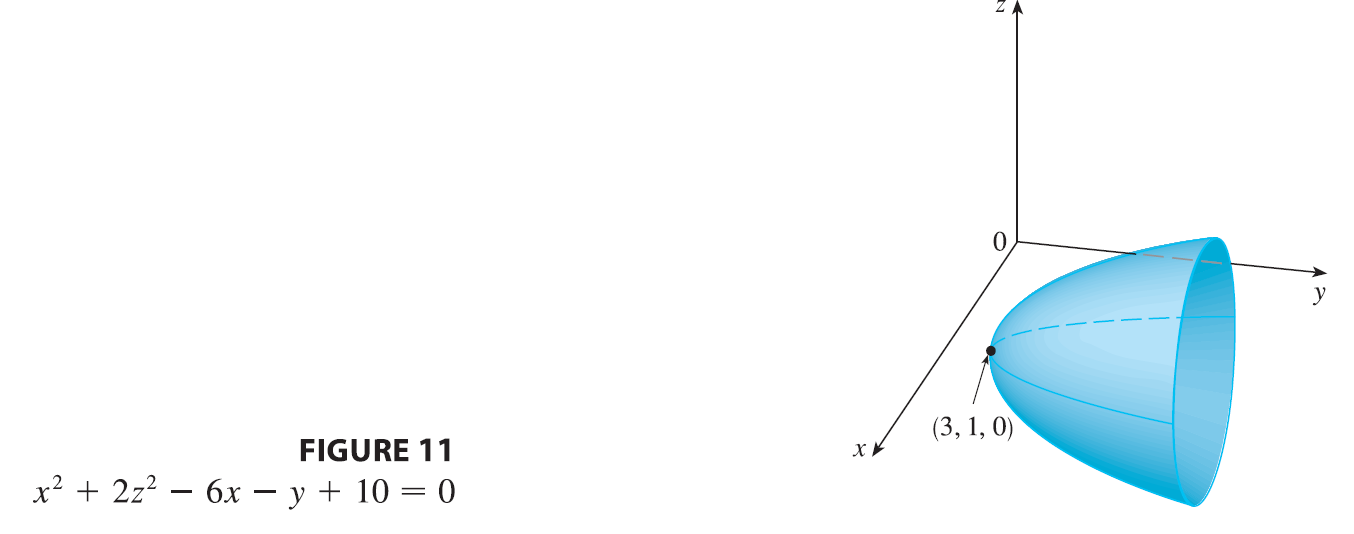Section 12.6: Cylinders & Quadric Surfaces
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 12.6: Cylinders & Quadric Surfaces |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 2:12 AM |
Table of contents
- 1. Cylinders
- 2. Quadric Surfaces
- 3. Combined discussion
- 4. Applications of Quadric Surfaces
- 5. Exercise 1
- 6. Exercise 2
- 7. Exercise 3
- 8. Exercise 4
- 9. Exercise 5
- 10. Exercise 6
- 11. Exercise 7
- 12. Exercise 8
- 13. Exercise 9
- 14. Exercise 10
- 15. Exercise 11
- 16. Exercise 12
- 17. Exercise 13
- 18. Exercise 14
- 19. Exercise 15
- 20. Exercise 16
- 21. Exercise 17
- 22. Exercise 18
- 23. Exercise 19
- 24. Exercise 20
- 25. Exercise 21
- 26. Exercise 22
- 27. Exercise 23
- 28. Exercise 24
- 29. Exercise 25
- 30. Exercise 26
- 31. Exercise 27
- 32. Exercise 28
- 33. Exercise 29
- 34. Exercise 30
- 35. Exercise 31
- 36. Exercise 32
- 37. Exercise 33
- 38. Exercise 34
- 39. Exercise 35
- 40. Exercise 36
- 41. Exercise 37
- 42. Exercise 38
- 43. Exercise 39
- 44. Exercise 40
- 45. Exercise 41
- 46. Exercise 42
- 47. Exercise 43
- 48. Exercise 44
- 49. Exercise 45
- 50. Exercise 46
- 51. Exercise 47
- 52. Exercise 48
- 53. Exercise 49
- 54. Exercise 50
- 55. Exercise 51
- 56. Exercise 52
- 57. Exercise 53
1. Cylinders
We have already looked at two special types of surfaces: planes (in Section 12.5) and spheres (in Section 12.1). Here we investigate two other types of surfaces: cylinders and quadric surfaces.
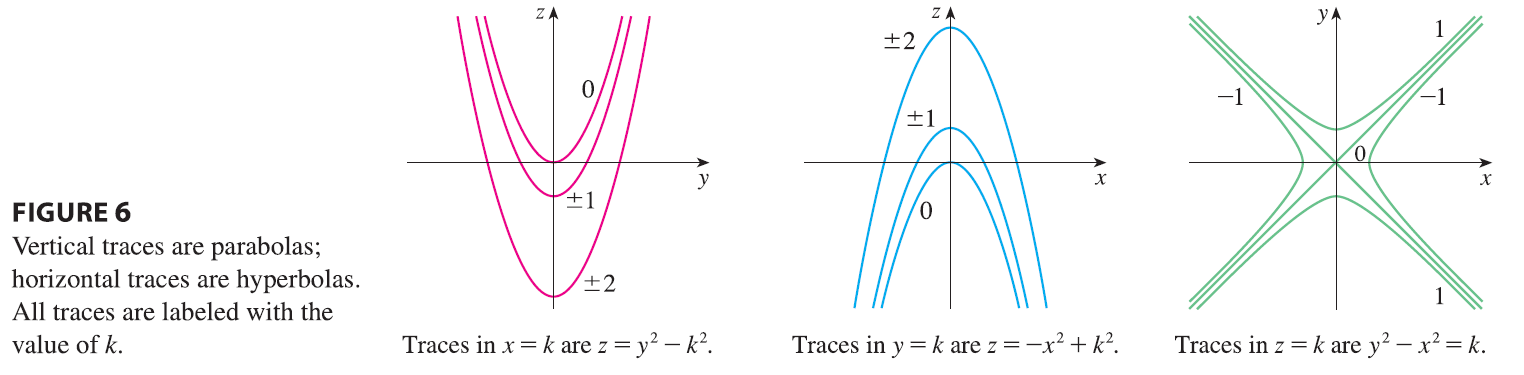
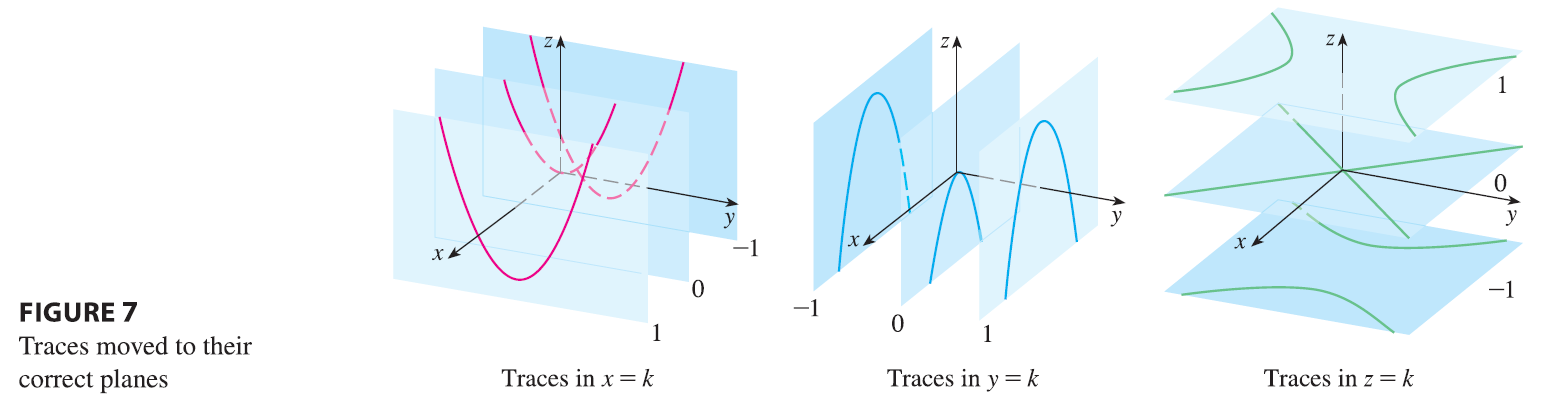
In order to sketch the graph of a surface, it is useful to determine the curves of intersection of the surface with planes parallel to the coordinate planes. These curves are called traces (or cross-sections) of the surface.
Cylinders
A cylinder is a surface that consists of all lines (called rulings) that are parallel to a given line and pass through a given plane curve.
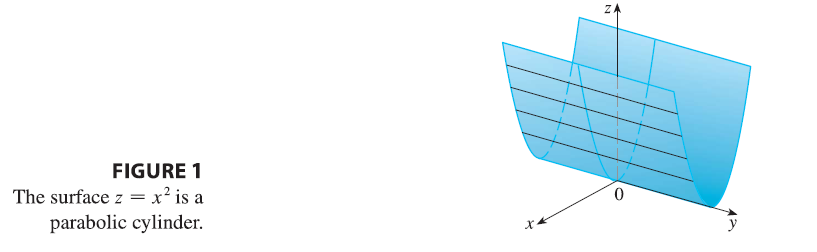
EXAMPLE 1 Sketch the graph of the surface \(z = x^2\).
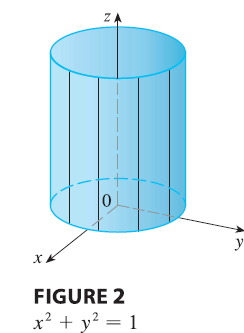
EXAMPLE 2 Identify and sketch the surfaces. (a) \(x^2 + y^2 = 1\) (b) \(y^2 + z^2 = 1\)
NOTE When you are dealing with surfaces, it is important to recognize that an equation like \(x^2 + y^2 = 1\) represents a cylinder and not a circle. The trace of the cylinder \(x^2 + y^2 = 1\) in the xy-plane is the circle with equations \(x^2 + y^2 = 1\), \(z = 0\).
2. Quadric Surfaces
A quadric surface is the graph of a second-degree equation in three variables \(x\), \(y\), and \(z\). The most general such equation is \[Ax^2 + By^2 + Cz^2 + Dxy + Eyz + Fxz + Gx + Hy + Iz + J = 0\] where A, B, C, …, J are constants, but by translation and rotation it can be brought into one of the two standard forms \[Ax^2 + By^2 + Cz^2 + J = 0 \quad \text{or} \quad Ax^2 + By^2 + Iz = 0\]
Quadric surfaces are the counterparts in three dimensions of the conic sections in the plane.
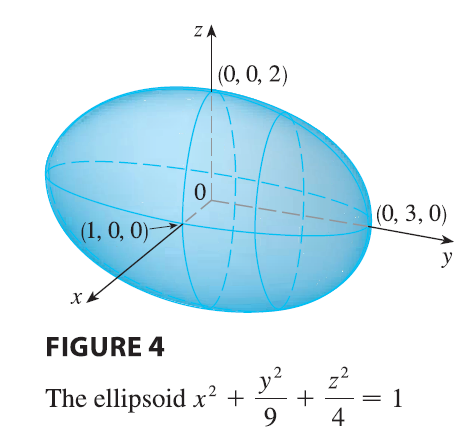
EXAMPLE 3 Use traces to sketch the quadric surface with equation \[x^2 + \frac{y^2}{9} + \frac{z^2}{4} = 1\]
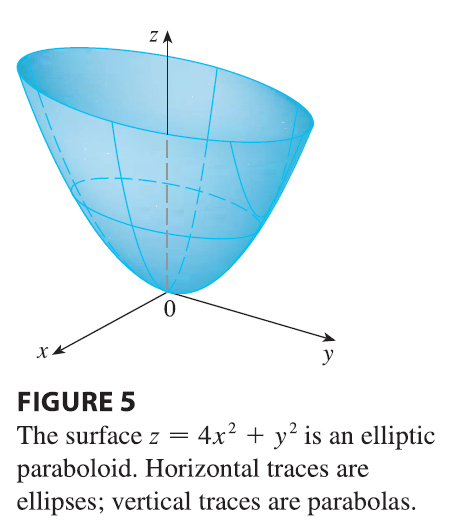
EXAMPLE 4 Use traces to sketch the surface \(z = 4x^2 + y^2\).
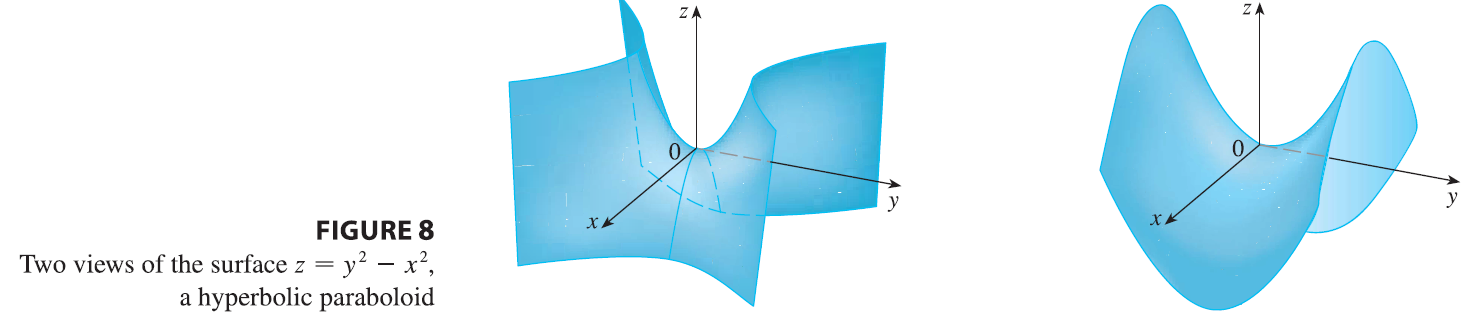
EXAMPLE 5 Sketch the surface \(z = y^2 - x^2\).
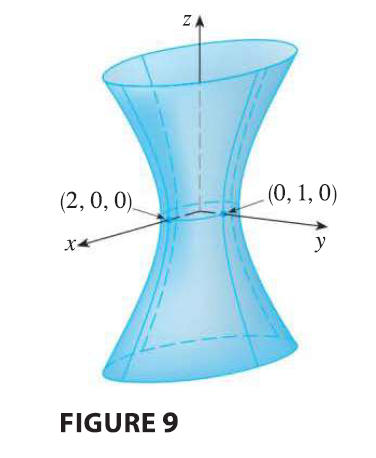
EXAMPLE 6 Sketch the surface \(\frac{x^2}{4} + y^2 - \frac{z^2}{4} = 1\).
3. Combined discussion
The idea of using traces to draw a surface is employed in three-dimensional graphing software. In most such software, traces in the vertical planes \(x = k\) and \(y = k\) are drawn for equally spaced values of \(k\), and parts of the graph are eliminated using hidden line removal. Table 1 shows computer-drawn graphs of the six basic types of quadric surfaces in standard form. All surfaces are symmetric with respect to the z-axis. If a quadric surface is symmetric about a different axis, its equation changes accordingly.

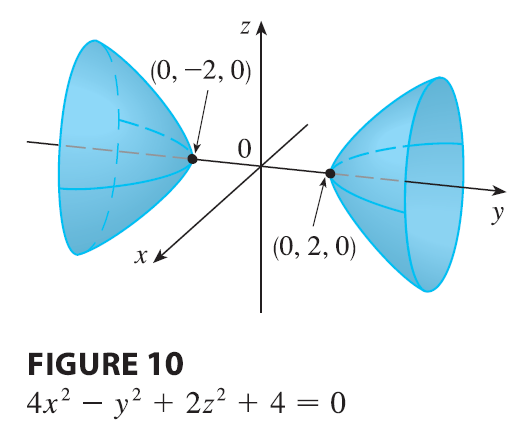
EXAMPLE 7 Identify and sketch the surface \(4x^2 - y^2 + 2z^2 + 4 = 0\).
EXAMPLE 8 Classify the quadric surface \(x^2 + 2z^2 - 6x - y + 10 = 0\).
4. Applications of Quadric Surfaces

Examples of quadric surfaces can be found in the world around us. In fact, the world itself is a good example. Although the earth is commonly modeled as a sphere, a more accurate model is an ellipsoid because the earth’s rotation has caused a flattening at the poles.
Circular paraboloids, obtained by rotating a parabola about its axis, are used to collect and reflect light, sound, and radio and television signals. In a radio telescope, for instance, signals from distant stars that strike the bowl are all reflected to the receiver at the focus and are therefore amplified. The same principle applies to microphones and satellite dishes in the shape of paraboloids.
Cooling towers for nuclear reactors are usually designed in the shape of hyperboloids of one sheet for reasons of structural stability. Pairs of hyperboloids are used to transmit rotational motion between skew axes. (The cogs of the gears are the generating lines of the hyperboloids.)
5. Exercise 1
- What does the equation \(y = x^2\) represent as a curve in \(\mathbb{R}^2\)?
- What does it represent as a surface in \(\mathbb{R}^3\)?
- What does the equation \(z = y^2\) represent?
6. Exercise 2
- Sketch the graph of \(y = e^x\) as a curve in \(\mathbb{R}^2\).
- Sketch the graph of \(y = e^x\) as a surface in \(\mathbb{R}^3\).
- Describe and sketch the surface \(z = e^y\).
7. Exercise 3
Describe and sketch the surface. \(x^2 + z^2 = 1\)
8. Exercise 4
Describe and sketch the surface. \(4x^2 + y^2 = 4\)
9. Exercise 5
Describe and sketch the surface. \(z = 1 - y^2\)
10. Exercise 6
Describe and sketch the surface. \(y = z^2\)
11. Exercise 7
Describe and sketch the surface. \(xy = 1\)
12. Exercise 8
Describe and sketch the surface. \(z = \sin y\)
13. Exercise 9
- Find and identify the traces of the quadric surface \(x^2 + y^2 - z^2 = 1\) and explain why the graph looks like the graph of the hyperboloid of one sheet in Table 1.
- If we change the equation in part (a) to \(x^2 - y^2 + z^2 = 1\), how is the graph affected?
- What if we change the equation in part (a) to \(x^2 + y^2 + 2y - z^2 = 0\)?
14. Exercise 10
- Find and identify the traces of the quadric surface \(-x^2 - y^2 + z^2 = 1\) and explain why the graph looks like the graph of the hyperboloid of two sheets in Table 1.
- If the equation in part (a) is changed to \(x^2 - y^2 - z^2 = 1\), what happens to the graph? Sketch the new graph.
15. Exercise 11
Use traces to sketch and identify the surface. \(x = y^2 + 4z^2\)
16. Exercise 12
Use traces to sketch and identify the surface. \(4x^2 + 9y^2 + 9z^2 = 36\)
17. Exercise 13
Use traces to sketch and identify the surface. \(x^2 = 4y^2 + z^2\)
18. Exercise 14
Use traces to sketch and identify the surface. \(z^2 - 4x^2 - y^2 = 4\)
19. Exercise 15
Use traces to sketch and identify the surface. \(9y^2 + 4z^2 = x^2 + 36\)
20. Exercise 16
Use traces to sketch and identify the surface. \(3x^2 + y + 3z^2 = 0\)
21. Exercise 17
Use traces to sketch and identify the surface. \(\frac{x^2}{9} + \frac{y^2}{25} + \frac{z^2}{4} = 1\)
22. Exercise 18
Use traces to sketch and identify the surface. \(3x^2 - y^2 + 3z^2 = 0\)
23. Exercise 19
Use traces to sketch and identify the surface. \(y = z^2 - x^2\)
24. Exercise 20
Use traces to sketch and identify the surface. \(x = y^2 - z^2\)
25. Exercise 21
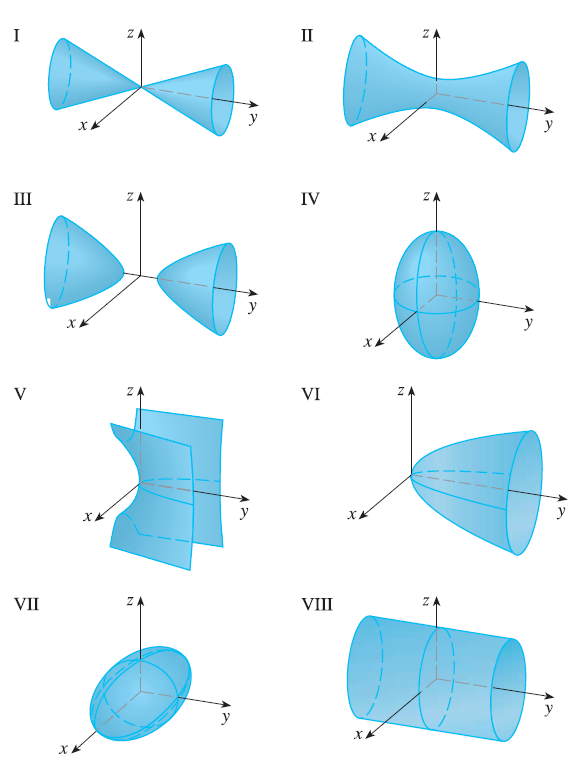
Match the equation with its graph (labeled I-VIII). Give reasons for your choice. \(x^2 + 4y^2 + 9z^2 = 1\)
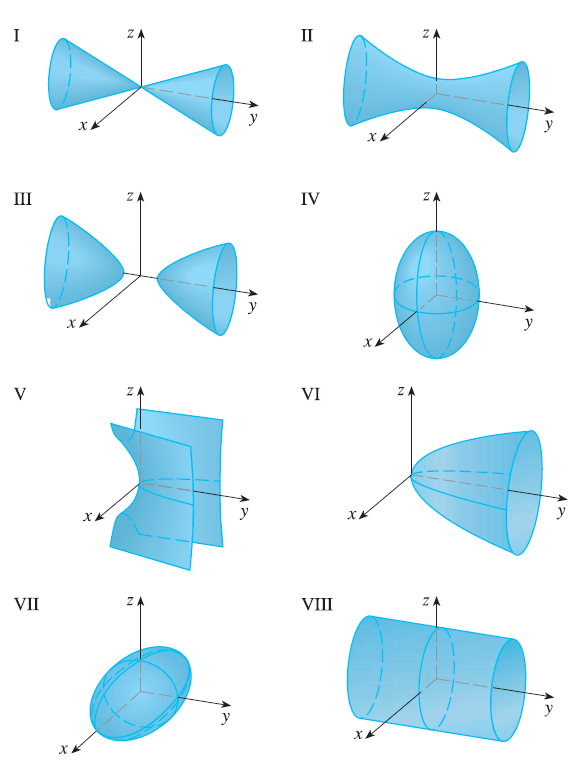
26. Exercise 22
Match the equation with its graph (labeled I-VIII). Give reasons for your choice. \(9x^2 + 4y^2 + z^2 = 1\)
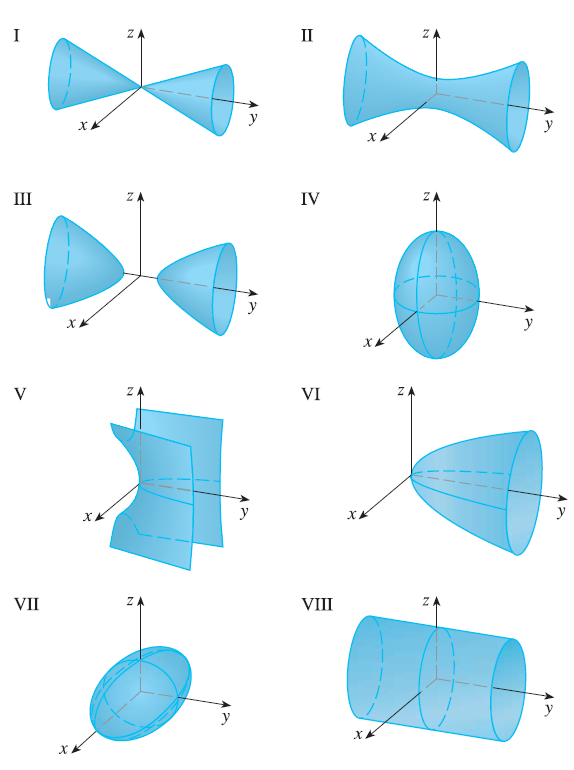
27. Exercise 23
Match the equation with its graph (labeled I-VIII). Give reasons for your choice. \(x^2 - y^2 + z^2 = 1\)
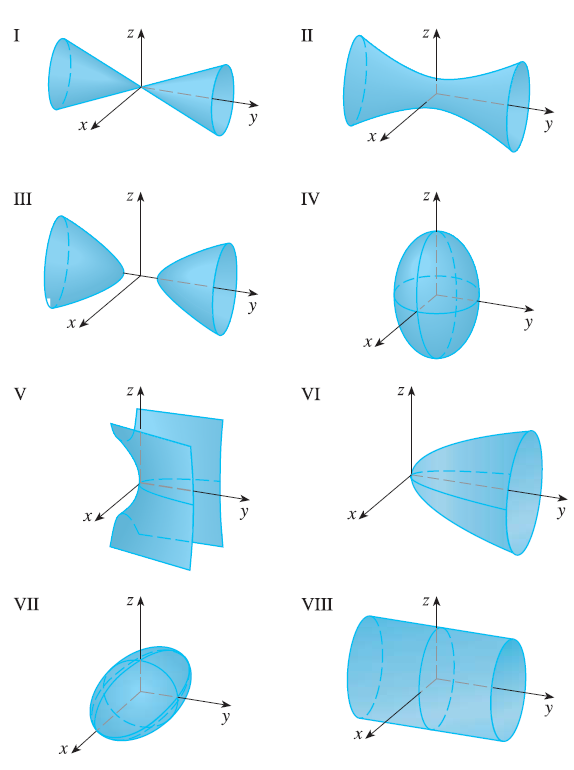
28. Exercise 24
Match the equation with its graph (labeled I-VIII). Give reasons for your choice. \(-x^2 + y^2 - z^2 = 1\)
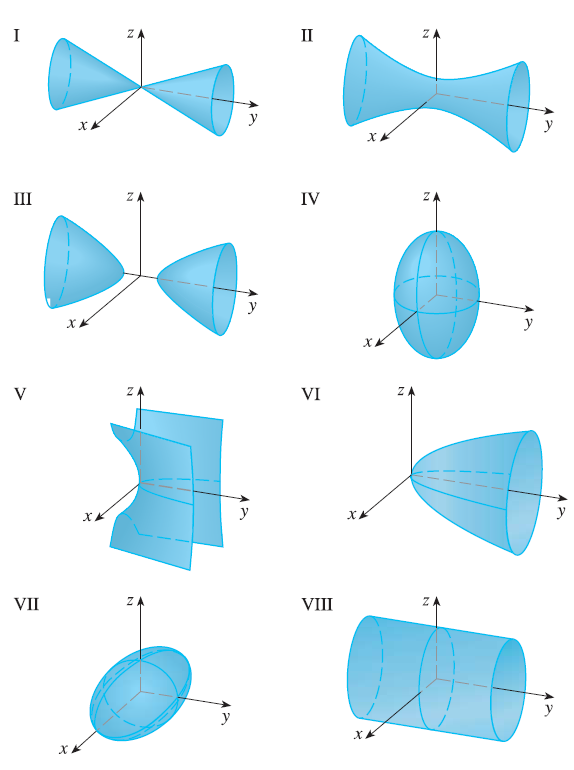
29. Exercise 25
Match the equation with its graph (labeled I-VIII). Give reasons for your choice. \(y = 2x^2 + z^2\)
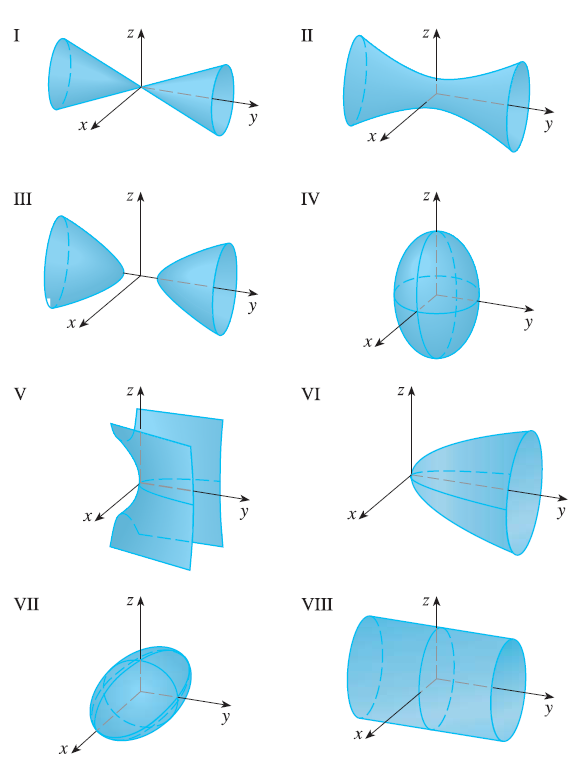
30. Exercise 26
Match the equation with its graph (labeled I-VIII). Give reasons for your choice. \(y^2 = x^2 + 2z^2\)
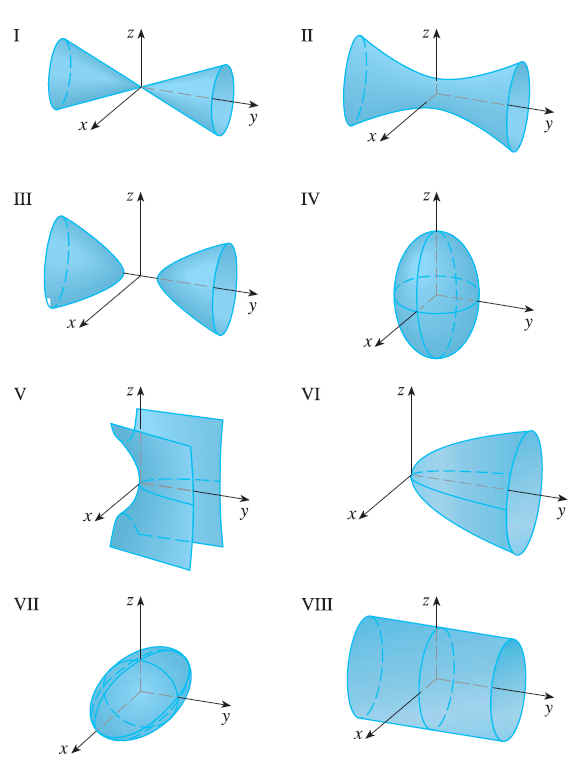
31. Exercise 27
Match the equation with its graph (labeled I-VIII). Give reasons for your choice. \(x^2 + 2z^2 = 1\)
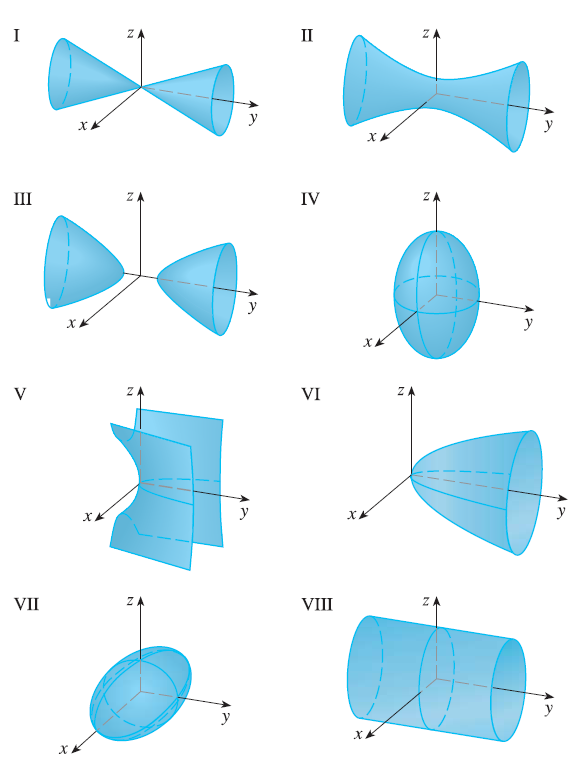
32. Exercise 28
Match the equation with its graph (labeled I-VIII). Give reasons for your choice. \(y = x^2 - z^2\)
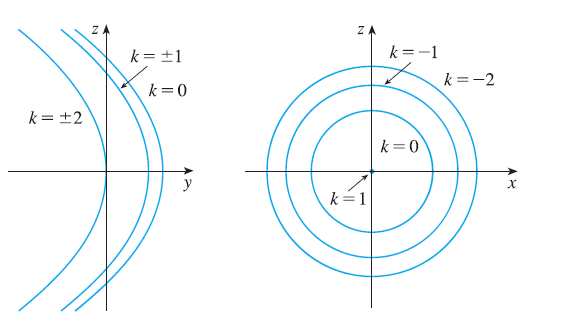
33. Exercise 29
Sketch and identify a quadric surface that could have the traces shown. Traces in \(x=k\) Traces in \(y=k\)
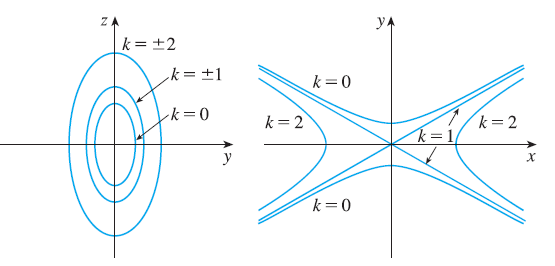
34. Exercise 30
Sketch and identify a quadric surface that could have the traces shown. Traces in \(x=k\) Traces in \(z=k\)
35. Exercise 31
Reduce the equation to one of the standard forms, classify the surface, and sketch it. \(y^2 = x^2 + 4z^2\)
36. Exercise 32
Reduce the equation to one of the standard forms, classify the surface, and sketch it. \(4x^2 - y + 2z^2 = 0\)
37. Exercise 33
Reduce the equation to one of the standard forms, classify the surface, and sketch it. \(x^2 + 2y - 2z^2 = 0\)
38. Exercise 34
Reduce the equation to one of the standard forms, classify the surface, and sketch it. \(y^2 = x^2 + 4z^2 + 4\)
39. Exercise 35
Reduce the equation to one of the standard forms, classify the surface, and sketch it. \(x^2 + y^2 - 2x - 6y - z + 10 = 0\)
40. Exercise 36
Reduce the equation to one of the standard forms, classify the surface, and sketch it. \(x^2 - y^2 - z^2 - 4x - 2z + 3 = 0\)
41. Exercise 37
Reduce the equation to one of the standard forms, classify the surface, and sketch it. \(x^2 - y^2 + z^2 - 4x - 2z = 0\)
42. Exercise 38
Reduce the equation to one of the standard forms, classify the surface, and sketch it. \(4x^2 + y^2 + z^2 - 24x - 8y + 4z + 55 = 0\)
43. Exercise 39
Use a computer with three-dimensional graphing software to graph the surface. Experiment with viewpoints and with domains for the variables until you get a good view of the surface. \(-4x^2 - y^2 + z^2 = 1\)
44. Exercise 40
Use a computer with three-dimensional graphing software to graph the surface. Experiment with viewpoints and with domains for the variables until you get a good view of the surface. \(x^2 - y^2 - z = 0\)
45. Exercise 41
Use a computer with three-dimensional graphing software to graph the surface. Experiment with viewpoints and with domains for the variables until you get a good view of the surface. \(-4x^2 - y^2 + z^2 = 0\)
46. Exercise 42
Use a computer with three-dimensional graphing software to graph the surface. Experiment with viewpoints and with domains for the variables until you get a good view of the surface. \(x^2 - 6x + 4y^2 - z = 0\)
47. Exercise 43
Sketch the region bounded by the surfaces \(z = \sqrt{x^2 + y^2}\) and \(x^2 + y^2 = 1\) for \(1 \le z \le 2\).
48. Exercise 44
Sketch the region bounded by the paraboloids \(z = x^2 + y^2\) and \(z = 2 - x^2 - y^2\).
49. Exercise 45
Find an equation for the surface obtained by rotating the curve \(y = \sqrt{x}\) about the x-axis.
50. Exercise 46
Find an equation for the surface obtained by rotating the line \(z = 2y\) about the z-axis.
51. Exercise 47
Find an equation for the surface consisting of all points that are equidistant from the point \((-1, 0, 0)\) and the plane \(x = 1\). Identify the surface.
52. Exercise 48
Find an equation for the surface consisting of all points P for which the distance from P to the x-axis is twice the distance from P to the yz-plane. Identify the surface.
53. Exercise 49
Traditionally, the earth’s surface has been modeled as a sphere, but the World Geodetic System of 1984 (WGS-84) uses an ellipsoid as a more accurate model. It places the center of the earth at the origin and the north pole on the positive z-axis. The distance from the center to the poles is 6356.523 km and the distance to a point on the equator is 6378.137 km. (a) Find an equation of the earth’s surface as used by WGS-84. (b) Curves of equal latitude are traces in the planes \(z = k\). What is the shape of these curves? (c) Meridians (curves of equal longitude) are traces in planes of the form \(y = mx\). What is the shape of these meridians?
54. Exercise 50
A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet (see the photo on page 839). The diameter at the base is 280 m and the minimum diameter, 500 m above the base, is 200 m. Find an equation for the tower.
55. Exercise 51
Show that if the point \((a, b, c)\) lies on the hyperbolic paraboloid \(z = y^2 - x^2\), then the lines with parametric equations \(x = a + t, y = b + t, z = c + 2(b-a)t\) and \(x = a + t, y = b - t, z = c - 2(b+a)t\) both lie entirely on this paraboloid. (This shows that the hyperbolic paraboloid is what is called a ruled surface; that is, it can be generated by the motion of a straight line. In fact, this exercise shows that through each point on the hyperbolic paraboloid there are two generating lines. The only other quadric surfaces that are ruled surfaces are cylinders, cones, and hyperboloids of one sheet.)
56. Exercise 52
Show that the curve of intersection of the surfaces \(x^2 + 2y^2 - z^2 + 3x = 1\) and \(2x^2 + 4y^2 - 2z^2 - 5y = 0\) lies in a plane.
57. Exercise 53
Graph the surfaces \(z = x^2 + y^2\) and \(z = 1 - y^2\) on a common screen using the domain \(|x| \le 1.2, |y| \le 1.2\) and observe the curve of intersection of these surfaces. Show that the projection of this curve onto the xy-plane is an ellipse.