Section 13.2: Derivatives and Integrals of Vector Functions
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 13.2: Derivatives and Integrals of Vector Functions |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 3:57 AM |
Table of contents
- Derivatives of Vector Functions
- Second derivatives
- Differentiation Rules
- Example
- Integrals
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
- Exercise 49
- Exercise 50
- Exercise 51
- Exercise 52
- Exercise 53
- Exercise 54
- Exercise 55
- Exercise 56
- Exercise 57
- Exercise 58
Derivatives of Vector Functions
Later in this chapter we are going to use vector functions to describe the motion of planets and other objects through space. Here we prepare the way by developing the calculus of vector functions.
Derivatives
The derivative \(\mathbf{r}'\) of a vector function \(\mathbf{r}\) is defined in much the same way as for real-valued functions:
\[ \frac{d\mathbf{r}}{dt} = \mathbf{r}'(t) = \lim_{h \to 0} \frac{\mathbf{r}(t+h) - \mathbf{r}(t)}{h} \tag{1} \]
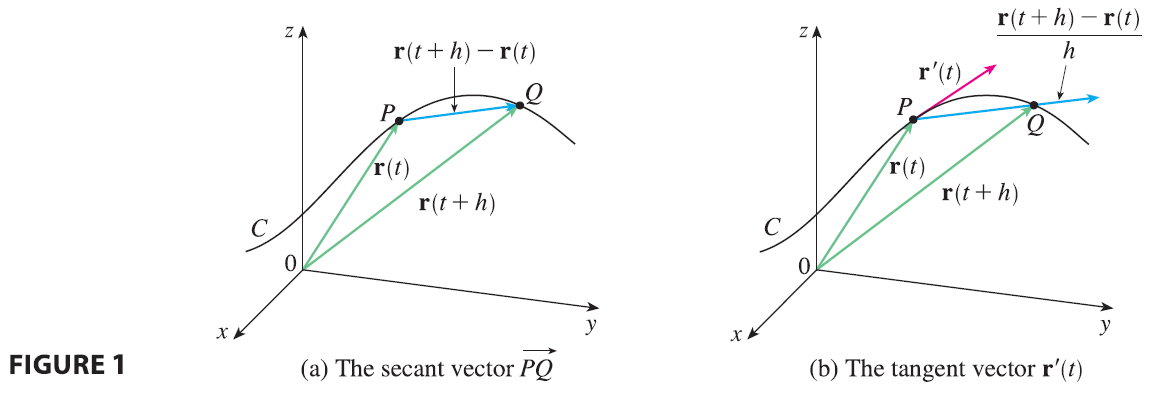
if this limit exists. The geometric significance of this definition is shown in Figure 1. If the points P and Q have position vectors \(\mathbf{r}(t)\) and \(\mathbf{r}(t+h)\), then \(\vec{PQ}\) represents the vector \(\mathbf{r}(t+h) - \mathbf{r}(t)\), which can therefore be regarded as a secant vector. If \(h > 0\), the scalar multiple \((1/h)(\mathbf{r}(t+h) - \mathbf{r}(t))\) has the same direction as \(\mathbf{r}(t+h) - \mathbf{r}(t)\). As \(h \to 0\), it appears that this vector approaches a vector that lies on the tangent line. For this reason, the vector \(\mathbf{r}'(t)\) is called the tangent vector to the curve defined by \(\mathbf{r}\) at the point P, provided that \(\mathbf{r}'(t)\) exists and \(\mathbf{r}'(t) \neq \mathbf{0}\). The tangent line to C at P is defined to be the line through P parallel to the tangent vector \(\mathbf{r}'(t)\). We will also have occasion to consider the unit tangent vector, which is
\[ \mathbf{T}(t) = \frac{\mathbf{r}'(t)}{|\mathbf{r}'(t)|} \]
The following theorem gives us a convenient method for computing the derivative of a vector function \(\mathbf{r}\): just differentiate each component of \(\mathbf{r}\).
Theorem 2 If \(\mathbf{r}(t) = \langle f(t), g(t), h(t) \rangle = f(t)\mathbf{i} + g(t)\mathbf{j} + h(t)\mathbf{k}\), where f, g, and h are differentiable functions, then \[ \mathbf{r}'(t) = \langle f'(t), g'(t), h'(t) \rangle = f'(t)\mathbf{i} + g'(t)\mathbf{j} + h'(t)\mathbf{k} \]
PROOF \[ \mathbf{r}'(t) = \lim_{\Delta t \to 0} \frac{1}{\Delta t}[\mathbf{r}(t+\Delta t) - \mathbf{r}(t)] \] \[ = \lim_{\Delta t \to 0} \frac{1}{\Delta t}[\langle f(t+\Delta t), g(t+\Delta t), h(t+\Delta t) \rangle - \langle f(t), g(t), h(t) \rangle] \] \[ = \lim_{\Delta t \to 0} \left\langle \frac{f(t+\Delta t) - f(t)}{\Delta t}, \frac{g(t+\Delta t) - g(t)}{\Delta t}, \frac{h(t+\Delta t) - h(t)}{\Delta t} \right\rangle \] \[ = \left\langle \lim_{\Delta t \to 0} \frac{f(t+\Delta t) - f(t)}{\Delta t}, \lim_{\Delta t \to 0} \frac{g(t+\Delta t) - g(t)}{\Delta t}, \lim_{\Delta t \to 0} \frac{h(t+\Delta t) - h(t)}{\Delta t} \right\rangle \] \[ = \langle f'(t), g'(t), h'(t) \rangle \]
EXAMPLE 1 (a) Find the derivative of \(\mathbf{r}(t) = (1+t^3)\mathbf{i} + te^{-t}\mathbf{j} + \sin 2t \mathbf{k}\). (b) Find the unit tangent vector at the point where \(t=0\).
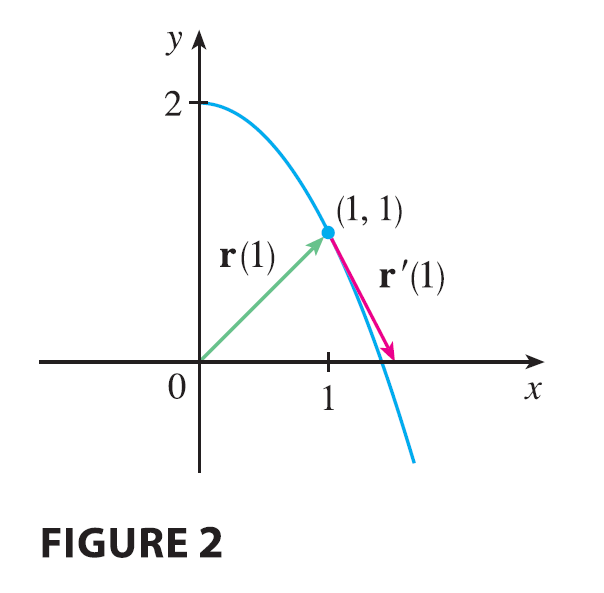
EXAMPLE 2 For the curve \(\mathbf{r}(t) = \sqrt{t}\mathbf{i} + (2-t)\mathbf{j}\), find \(\mathbf{r}'(t)\) and sketch the position vector \(\mathbf{r}(1)\) and the tangent vector \(\mathbf{r}'(1)\).
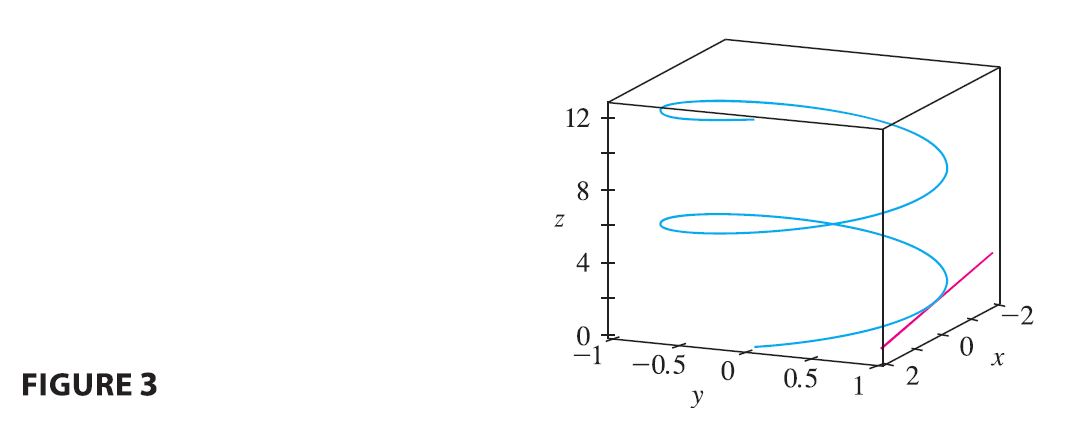
EXAMPLE 3 Find parametric equations for the tangent line to the helix with parametric equations \[ x = 2\cos t \quad y = \sin t \quad z=t \] at the point \((0, 1, \pi/2)\).
Second derivatives
Just as for real-valued functions, the second derivative of a vector function \(\mathbf{r}\) is the derivative of \(\mathbf{r}'\), that is, \(\mathbf{r}'' = (\mathbf{r}')'\). For instance, the second derivative of the function in Example 3 is \[ \mathbf{r}''(t) = \langle -2\cos t, -\sin t, 0 \rangle \]
Differentiation Rules
The next theorem shows that the differentiation formulas for real-valued functions have their counterparts for vector-valued functions.
Theorem 3 Suppose \(\mathbf{u}\) and \(\mathbf{v}\) are differentiable vector functions, c is a scalar, and f is a real-valued function. Then 1. \(\frac{d}{dt}[\mathbf{u}(t) + \mathbf{v}(t)] = \mathbf{u}'(t) + \mathbf{v}'(t)\) 2. \(\frac{d}{dt}[c\mathbf{u}(t)] = c\mathbf{u}'(t)\) 3. \(\frac{d}{dt}[f(t)\mathbf{u}(t)] = f'(t)\mathbf{u}(t) + f(t)\mathbf{u}'(t)\) 4. \(\frac{d}{dt}[\mathbf{u}(t) \cdot \mathbf{v}(t)] = \mathbf{u}'(t) \cdot \mathbf{v}(t) + \mathbf{u}(t) \cdot \mathbf{v}'(t)\) 5. \(\frac{d}{dt}[\mathbf{u}(t) \times \mathbf{v}(t)] = \mathbf{u}'(t) \times \mathbf{v}(t) + \mathbf{u}(t) \times \mathbf{v}'(t)\) 6. \(\frac{d}{dt}[\mathbf{u}(f(t))] = f'(t)\mathbf{u}'(f(t))\) (Chain Rule)
This theorem can be proved either directly from Definition 1 or by using Theorem 2 and the corresponding differentiation formulas for real-valued functions. The proof of Formula 4 follows; the remaining formulas are left as exercises.
PROOF OF FORMULA 4 Let \[ \mathbf{u}(t) = \langle f_1(t), f_2(t), f_3(t) \rangle \quad \mathbf{v}(t) = \langle g_1(t), g_2(t), g_3(t) \rangle \] Then \[ \mathbf{u}(t) \cdot \mathbf{v}(t) = f_1(t)g_1(t) + f_2(t)g_2(t) + f_3(t)g_3(t) = \sum_{i=1}^3 f_i(t)g_i(t) \] so the ordinary Product Rule gives \[ \frac{d}{dt}[\mathbf{u}(t) \cdot \mathbf{v}(t)] = \frac{d}{dt} \sum_{i=1}^3 f_i(t)g_i(t) = \sum_{i=1}^3 \frac{d}{dt}[f_i(t)g_i(t)] \] \[ = \sum_{i=1}^3 [f_i'(t)g_i(t) + f_i(t)g_i'(t)] \] \[ = \sum_{i=1}^3 f_i'(t)g_i(t) + \sum_{i=1}^3 f_i(t)g_i'(t) \] \[ = \mathbf{u}'(t) \cdot \mathbf{v}(t) + \mathbf{u}(t) \cdot \mathbf{v}'(t) \]
Example
EXAMPLE 4 Show that if \(|\mathbf{r}(t)| = c\) (a constant), then \(\mathbf{r}'(t)\) is orthogonal to \(\mathbf{r}(t)\) for all t.
Integrals
The definite integral of a continuous vector function \(\mathbf{r}(t)\) can be defined in much the same way as for real-valued functions except that the integral is a vector. But then we can express the integral of \(\mathbf{r}\) in terms of the integrals of its component functions f, g, and h as follows.
\[ \int_a^b \mathbf{r}(t) dt = \lim_{n \to \infty} \sum_{i=1}^n \mathbf{r}(t_i^*) \Delta t \] \[ = \lim_{n \to \infty} \left[ \left( \sum_{i=1}^n f(t_i^*) \Delta t \right)\mathbf{i} + \left( \sum_{i=1}^n g(t_i^*) \Delta t \right)\mathbf{j} + \left( \sum_{i=1}^n h(t_i^*) \Delta t \right)\mathbf{k} \right] \] and so \[ \int_a^b \mathbf{r}(t) dt = \left( \int_a^b f(t) dt \right)\mathbf{i} + \left( \int_a^b g(t) dt \right)\mathbf{j} + \left( \int_a^b h(t) dt \right)\mathbf{k} \] This means that we can evaluate an integral of a vector function by integrating each component function. We can extend the Fundamental Theorem of Calculus to continuous vector functions as follows: \[ \int_a^b \mathbf{r}(t) dt = \mathbf{R}(t) \Big]_a^b = \mathbf{R}(b) - \mathbf{R}(a) \] where \(\mathbf{R}\) is an antiderivative of \(\mathbf{r}\), that is, \(\mathbf{R}'(t) = \mathbf{r}(t)\). We use the notation \(\int \mathbf{r}(t) dt\) for indefinite integrals (antiderivatives).
EXAMPLE 5 If \(\mathbf{r}(t) = 2\cos t \mathbf{i} + \sin t \mathbf{j} + 2t \mathbf{k}\), then \[ \int \mathbf{r}(t) dt = \left( \int 2\cos t dt \right)\mathbf{i} + \left( \int \sin t dt \right)\mathbf{j} + \left( \int 2t dt \right)\mathbf{k} \] \[ = 2\sin t \mathbf{i} - \cos t \mathbf{j} + t^2 \mathbf{k} + \mathbf{C} \] where \(\mathbf{C}\) is a vector constant of integration, and \[ \int_0^{\pi/2} \mathbf{r}(t) dt = [2\sin t \mathbf{i} - \cos t \mathbf{j} + t^2 \mathbf{k}]_0^{\pi/2} = 2\mathbf{i} + \mathbf{j} + \frac{\pi^2}{4}\mathbf{k} \]
Exercise 1
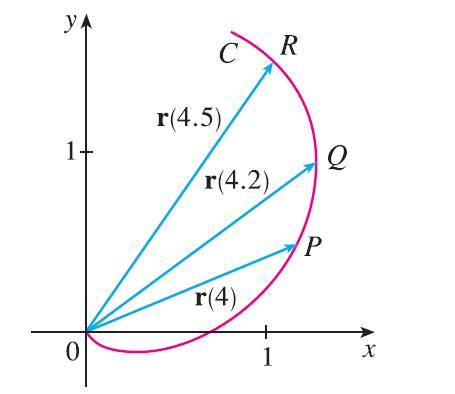
The figure shows a curve C given by a vector function \(\mathbf{r}(t)\). (a) Draw the vectors \(\mathbf{r}(4.5) - \mathbf{r}(4)\) and \(\mathbf{r}(4.2) - \mathbf{r}(4)\). (b) Draw the vectors \[ \frac{\mathbf{r}(4.5) - \mathbf{r}(4)}{0.5} \quad \text{and} \quad \frac{\mathbf{r}(4.2) - \mathbf{r}(4)}{0.2} \] (c) Write expressions for \(\mathbf{r}'(4)\) and the unit tangent vector \(\mathbf{T}(4)\). (d) Draw the vector \(\mathbf{T}(4)\).
Exercise 2
- Make a large sketch of the curve described by the vector function \(\mathbf{r}(t) = \langle t^2, t \rangle\), \(0 \le t \le 2\), and draw the vectors \(\mathbf{r}(1)\), \(\mathbf{r}(1.1)\), and \(\mathbf{r}(1.1) - \mathbf{r}(1)\).
- Draw the vector \(\mathbf{r}'(1)\) starting at (1, 1), and compare it with the vector \[ \frac{\mathbf{r}(1.1) - \mathbf{r}(1)}{0.1} \] Explain why these vectors are so close to each other in length and direction.
Exercise 3
- Sketch the plane curve with the given vector equation.
- Find \(\mathbf{r}'(t)\).
- Sketch the position vector \(\mathbf{r}(t)\) and the tangent vector \(\mathbf{r}'(t)\) for the given value of t. \(\mathbf{r}(t) = \langle t-2, t^2+1 \rangle, t=-1\)
Exercise 4
- Sketch the plane curve with the given vector equation.
- Find \(\mathbf{r}'(t)\).
- Sketch the position vector \(\mathbf{r}(t)\) and the tangent vector \(\mathbf{r}'(t)\) for the given value of t. \(\mathbf{r}(t) = \langle t^2, t^3 \rangle, t=1\)
Exercise 5
- Sketch the plane curve with the given vector equation.
- Find \(\mathbf{r}'(t)\).
- Sketch the position vector \(\mathbf{r}(t)\) and the tangent vector \(\mathbf{r}'(t)\) for the given value of t. \(\mathbf{r}(t) = e^{2t}\mathbf{i} + e^t\mathbf{j}, t=0\)
Exercise 6
- Sketch the plane curve with the given vector equation.
- Find \(\mathbf{r}'(t)\).
- Sketch the position vector \(\mathbf{r}(t)\) and the tangent vector \(\mathbf{r}'(t)\) for the given value of t. \(\mathbf{r}(t) = e^t\mathbf{i} + 2t\mathbf{j}, t=0\)
Exercise 7
- Sketch the plane curve with the given vector equation.
- Find \(\mathbf{r}'(t)\).
- Sketch the position vector \(\mathbf{r}(t)\) and the tangent vector \(\mathbf{r}'(t)\) for the given value of t. \(\mathbf{r}(t) = 4\sin t \mathbf{i} - 2\cos t \mathbf{j}, t=3\pi/4\)
Exercise 8
- Sketch the plane curve with the given vector equation.
- Find \(\mathbf{r}'(t)\).
- Sketch the position vector \(\mathbf{r}(t)\) and the tangent vector \(\mathbf{r}'(t)\) for the given value of t. \(\mathbf{r}(t) = (\cos t + 1)\mathbf{i} + (\sin t - 1)\mathbf{j}, t=-\pi/3\)
Exercise 9
Find the derivative of the vector function. \(\mathbf{r}(t) = \langle \sqrt{t}-2, 3, 1/t^2 \rangle\)
Exercise 10
Find the derivative of the vector function. \(\mathbf{r}(t) = \langle e^t, t-t^3, \ln t \rangle\)
Exercise 11
Find the derivative of the vector function. \(\mathbf{r}(t) = t^2\mathbf{i} + \cos(t^2)\mathbf{j} + \sin^2 t \mathbf{k}\)
Exercise 12
Find the derivative of the vector function. \(\mathbf{r}(t) = \frac{1}{1+t}\mathbf{i} + \frac{t}{1+t}\mathbf{j} + \frac{t^2}{1+t}\mathbf{k}\)
Exercise 13
Find the derivative of the vector function. \(\mathbf{r}(t) = t\sin t \mathbf{i} + e^t\cos t \mathbf{j} + \sin t \cos t \mathbf{k}\)
Exercise 14
Find the derivative of the vector function. \(\mathbf{r}(t) = \sin^2(at)\mathbf{i} + te^{bt}\mathbf{j} + \cos^2(ct)\mathbf{k}\)
Exercise 15
Find the derivative of the vector function. \(\mathbf{r}(t) = \mathbf{a} + t\mathbf{b} + t^2\mathbf{c}\)
Exercise 16
Find the derivative of the vector function. \(\mathbf{r}(t) = t\mathbf{a} \times (\mathbf{b} + t\mathbf{c})\)
Exercise 17
Find the unit tangent vector \(\mathbf{T}(t)\) at the point with the given value of the parameter t. \(\mathbf{r}(t) = \langle t^2-2t, 1+3t, \frac{1}{3}t^3 + \frac{1}{2}t^2 \rangle, t=2\)
Exercise 18
Find the unit tangent vector \(\mathbf{T}(t)\) at the point with the given value of the parameter t. \(\mathbf{r}(t) = \langle \tan^{-1} t, 2e^{2t}, 8te^t \rangle, t=0\)
Exercise 19
Find the unit tangent vector \(\mathbf{T}(t)\) at the point with the given value of the parameter t. \(\mathbf{r}(t) = \cos t \mathbf{i} + 3t \mathbf{j} + 2\sin 2t \mathbf{k}, t=0\)
Exercise 20
Find the unit tangent vector \(\mathbf{T}(t)\) at the point with the given value of the parameter t. \(\mathbf{r}(t) = \sin^2 t \mathbf{i} + \cos^2 t \mathbf{j} + \tan^2 t \mathbf{k}, t=\pi/4\)
Exercise 21
If \(\mathbf{r}(t) = \langle t, t^2, t^3 \rangle\), find \(\mathbf{r}'(t)\), \(\mathbf{T}(1)\), \(\mathbf{r}''(t)\), and \(\mathbf{r}'(t) \times \mathbf{r}''(t)\).
Exercise 22
If \(\mathbf{r}(t) = \langle e^{2t}, e^{-2t}, te^{2t} \rangle\), find \(\mathbf{T}(0)\), \(\mathbf{r}''(0)\), and \(\mathbf{r}'(t) \cdot \mathbf{r}''(t)\).
Exercise 23
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point. \(x = t^2+1, y=4\sqrt{t}, z=e^{t^2-t}; (2, 4, 1)\)
Exercise 24
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point. \(x = \ln(t+1), y=t\cos 2t, z=2^t; (0, 0, 1)\)
Exercise 25
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point. \(x = e^{-t}\cos t, y=e^{-t}\sin t, z=e^{-t}; (1, 0, 1)\)
Exercise 26
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point. \(x = \sqrt{t^2+3}, y=\ln(t^2+3), z=t; (2, \ln 4, 1)\)
Exercise 27
Find a vector equation for the tangent line to the curve of intersection of the cylinders \(x^2+y^2=25\) and \(y^2+z^2=20\) at the point \((3, 4, 2)\).
Exercise 28
Find the point on the curve \(\mathbf{r}(t) = \langle 2\cos t, 2\sin t, e^t \rangle\), \(0 \le t \le \pi\), where the tangent line is parallel to the plane \(\sqrt{3}x+y=1\).
Exercise 29
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point. Illustrate by graphing both the curve and the tangent line on a common screen. \(x=t, y=e^{-t}, z=2t-t^2; (0, 1, 0)\)
Exercise 30
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point. Illustrate by graphing both the curve and the tangent line on a common screen. \(x=2\cos t, y=2\sin t, z=4\cos 2t; (\sqrt{3}, 1, 2)\)
Exercise 31
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point. Illustrate by graphing both the curve and the tangent line on a common screen. \(x=t\cos t, y=t, z=t\sin t; (-\pi, \pi, 0)\)
Exercise 32
- Find the point of intersection of the tangent lines to the curve \(\mathbf{r}(t) = \langle \sin \pi t, 2\sin \pi t, \cos \pi t \rangle\) at the points where \(t=0\) and \(t=0.5\).
- Illustrate by graphing the curve and both tangent lines.
Exercise 33
The curves \(\mathbf{r}_1(t) = \langle t, t^2, t^3 \rangle\) and \(\mathbf{r}_2(t) = \langle \sin t, \sin 2t, t \rangle\) intersect at the origin. Find their angle of intersection correct to the nearest degree.
Exercise 34
At what point do the curves \(\mathbf{r}_1(t) = \langle t, 1-t, 3+t^2 \rangle\) and \(\mathbf{r}_2(s) = \langle 3-s, s-2, s^2 \rangle\) intersect? Find their angle of intersection correct to the nearest degree.
Exercise 35
Evaluate the integral. \(\int_0^2 (t\mathbf{i} - t^3\mathbf{j} + 3t^5\mathbf{k}) dt\)
Exercise 36
Evaluate the integral. \(\int_0^1 (t^{3/2}\mathbf{i} + (t+1)\sqrt{t}\mathbf{k}) dt\)
Exercise 37
Evaluate the integral. \(\int_0^1 \left( \frac{1}{t+1}\mathbf{i} + \frac{1}{t^2+1}\mathbf{j} + \frac{t}{t^2+1}\mathbf{k} \right) dt\)
Exercise 38
Evaluate the integral. \(\int_0^{\pi/4} (\sec t \tan t \mathbf{i} + t\cos 2t \mathbf{j} + \sin^2 2t \cos 2t \mathbf{k}) dt\)
Exercise 39
Evaluate the integral. \(\int (\sec^2 t \mathbf{i} + t(t^2+1)^3\mathbf{j} + t^2\ln t \mathbf{k}) dt\)
Exercise 40
Evaluate the integral. \(\int \left( te^{2t}\mathbf{i} + \frac{t}{1-t}\mathbf{j} + \frac{1}{\sqrt{1-t^2}}\mathbf{k} \right) dt\)
Exercise 41
Find \(\mathbf{r}(t)\) if \(\mathbf{r}'(t) = 2t\mathbf{i} + 3t^2\mathbf{j} + \sqrt{t}\mathbf{k}\) and \(\mathbf{r}(1) = \mathbf{i} + \mathbf{j}\).
Exercise 42
Find \(\mathbf{r}(t)\) if \(\mathbf{r}'(t) = t\mathbf{i} + e^t\mathbf{j} + te^t\mathbf{k}\) and \(\mathbf{r}(0) = \mathbf{i} + \mathbf{j} + \mathbf{k}\).
Exercise 43
Prove Formula 1 of Theorem 3.
Exercise 44
Prove Formula 3 of Theorem 3.
Exercise 45
Prove Formula 5 of Theorem 3.
Exercise 46
Prove Formula 6 of Theorem 3.
Exercise 47
If \(\mathbf{u}(t) = \langle \sin t, \cos t, t \rangle\) and \(\mathbf{v}(t) = \langle t, \cos t, \sin t \rangle\), use Formula 4 of Theorem 3 to find \(\frac{d}{dt}[\mathbf{u}(t) \cdot \mathbf{v}(t)]\)
Exercise 48
If \(\mathbf{u}\) and \(\mathbf{v}\) are the vector functions in Exercise 47, use Formula 5 of Theorem 3 to find \(\frac{d}{dt}[\mathbf{u}(t) \times \mathbf{v}(t)]\)
Exercise 49
Find \(f'(2)\), where \(f(t) = \mathbf{u}(t) \cdot \mathbf{v}(t)\), \(\mathbf{u}(2) = \langle 1, 2, -1 \rangle\), \(\mathbf{u}'(2) = \langle 3, 0, 4 \rangle\), and \(\mathbf{v}(t) = \langle t, t^2, t^3 \rangle\).
Exercise 50
If \(\mathbf{r}(t) = \mathbf{u}(t) \times \mathbf{v}(t)\), where \(\mathbf{u}\) and \(\mathbf{v}\) are the vector functions in Exercise 49, find \(\mathbf{r}'(2)\).
Exercise 51
If \(\mathbf{r}(t) = \mathbf{a}\cos \omega t + \mathbf{b}\sin \omega t\), where \(\mathbf{a}\) and \(\mathbf{b}\) are constant vectors, show that \(\mathbf{r}(t) \times \mathbf{r}'(t) = \omega \mathbf{a} \times \mathbf{b}\).
Exercise 52
If \(\mathbf{r}\) is the vector function in Exercise 51, show that \(\mathbf{r}''(t) + \omega^2\mathbf{r}(t) = \mathbf{0}\).
Exercise 53
Show that if \(\mathbf{r}\) is a vector function such that \(\mathbf{r}''\) exists, then \(\frac{d}{dt}[\mathbf{r}(t) \times \mathbf{r}'(t)] = \mathbf{r}(t) \times \mathbf{r}''(t)\)
Exercise 54
Find an expression for \(\frac{d}{dt}[\mathbf{u}(t) \cdot (\mathbf{v}(t) \times \mathbf{w}(t))]\).
Exercise 55
If \(\mathbf{r}(t) \neq \mathbf{0}\), show that \(\frac{d}{dt}|\mathbf{r}(t)| = \frac{1}{|\mathbf{r}(t)|}\mathbf{r}(t) \cdot \mathbf{r}'(t)\). [Hint: \(|\mathbf{r}(t)|^2 = \mathbf{r}(t) \cdot \mathbf{r}(t)\)]
Exercise 56
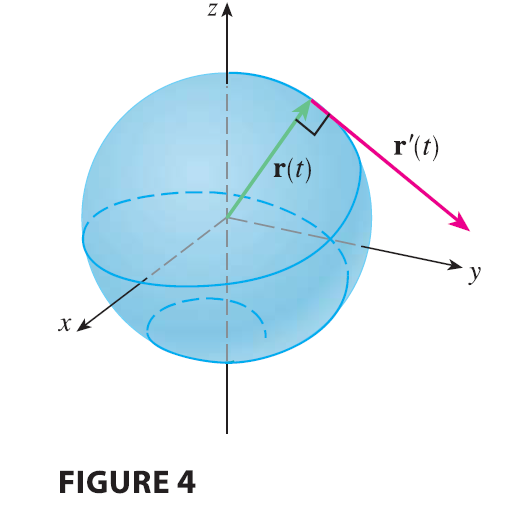
If a curve has the property that the position vector \(\mathbf{r}(t)\) is always perpendicular to the tangent vector \(\mathbf{r}'(t)\), show that the curve lies on a sphere with center the origin.
Exercise 57
If \(\mathbf{u}(t) = \mathbf{r}(t) \cdot [\mathbf{r}'(t) \times \mathbf{r}''(t)]\), show that \(\mathbf{u}'(t) = \mathbf{r}(t) \cdot [\mathbf{r}'(t) \times \mathbf{r}'''(t)]\)
Exercise 58
Show that the tangent vector to a curve defined by a vector function \(\mathbf{r}(t)\) points in the direction of increasing t. [Hint: Refer to Figure 1 and consider the cases \(h>0\) and \(h<0\) separately.]