Section 15.7: Triple Integration in Cylindrical Coordinates
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 15.7: Triple Integration in Cylindrical Coordinates |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 3:57 AM |
Table of contents
- Cylindrical Coordinates
- Equation of surfaces in Cylindrical Coordinates
- Evaluating Triple Integrals with Cylindrical Coordinates
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
Cylindrical Coordinates
In plane geometry the polar coordinate system is used to give a convenient description of certain curves and regions. (See Section 10.3.)
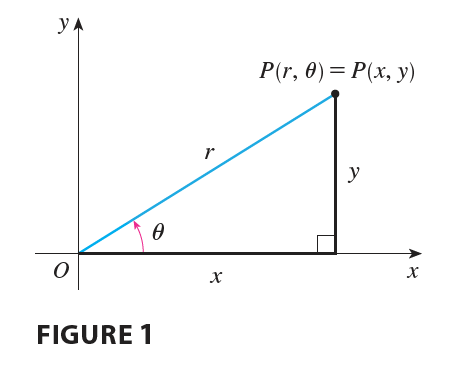
Figure 1 enables us to recall the connection between polar and Cartesian coordinates. If the point P has Cartesian coordinates \((x, y)\) and polar coordinates \((r, \theta)\), then, from the figure,
\[ x = r \cos \theta \qquad y = r \sin \theta \]
\[ r^2 = x^2 + y^2 \qquad \tan \theta = \frac{y}{x} \]
In three dimensions there is a coordinate system, called cylindrical coordinates, that is similar to polar coordinates and gives convenient descriptions of some commonly occurring surfaces and solids. As we will see, some triple integrals are much easier to evaluate in cylindrical coordinates.
Cylindrical Coordinates
In the cylindrical coordinate system, a point P in three-dimensional space is represented by the ordered triple \((r, \theta, z)\), where r and \(\theta\) are polar coordinates of the projection of P onto the xy-plane and z is the directed distance from the xy-plane to P. (See Figure 2.)
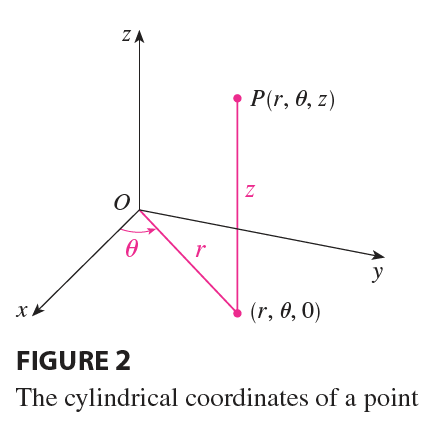
To convert from cylindrical to rectangular coordinates, we use the equations
\[ x = r \cos \theta \qquad y = r \sin \theta \qquad z = z \tag{1} \]
whereas to convert from rectangular to cylindrical coordinates, we use
\[ r^2 = x^2 + y^2 \qquad \tan \theta = \frac{y}{x} \qquad z = z \tag{2} \]
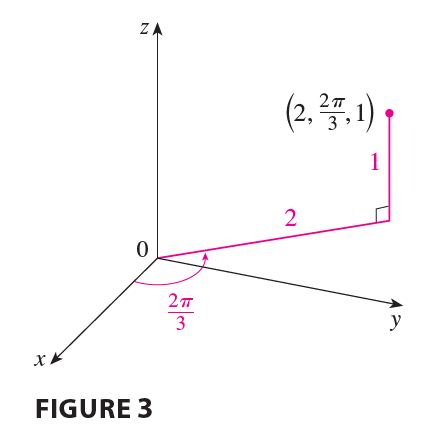
EXAMPLE 1 (a) Plot the point with cylindrical coordinates \((2, 2\pi/3, 1)\) and find its rectangular coordinates. (b) Find cylindrical coordinates of the point with rectangular coordinates \((3, -3, -7)\).
Equation of surfaces in Cylindrical Coordinates
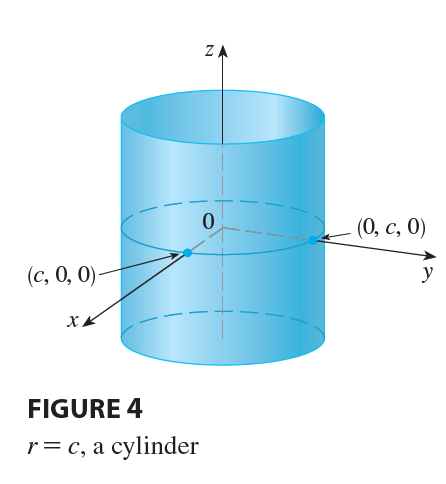
Cylindrical coordinates are useful in problems that involve symmetry about an axis, and the z-axis is chosen to coincide with this axis of symmetry. For instance, the axis of the circular cylinder with Cartesian equation \(x^2 + y^2 = c^2\) is the z-axis. In cylindrical coordinates this cylinder has the very simple equation \(r=c\). (See Figure 4.) This is the reason for the name “cylindrical” coordinates.
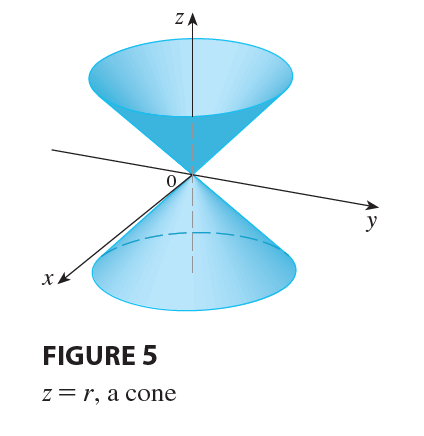
EXAMPLE 2 Describe the surface whose equation in cylindrical coordinates is \(z=r\).
Evaluating Triple Integrals with Cylindrical Coordinates
Suppose that E is a type 1 region whose projection D onto the xy-plane is conveniently described in polar coordinates (see Figure 6).
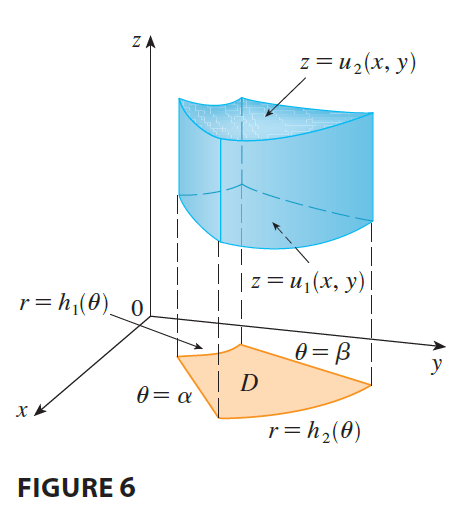
In particular, suppose that f is continuous and \[ E = \{(x, y, z) | (x, y) \in D, u_1(x, y) \le z \le u_2(x, y)\} \] where D is given in polar coordinates by \[ D = \{(r, \theta) | \alpha \le \theta \le \beta, h_1(\theta) \le r \le h_2(\theta)\} \] We know from Equation 15.6.6 that
\[ \iiint_E f(x, y, z) dV = \iint_D \left[ \int_{u_1(x,y)}^{u_2(x,y)} f(x, y, z) dz \right] dA \tag{3} \]
But we also know how to evaluate double integrals in polar coordinates. In fact, combining Equation 3 with Equation 15.3.3, we obtain
\[ \iiint_E f(x, y, z) dV = \int_\alpha^\beta \int_{h_1(\theta)}^{h_2(\theta)} \int_{u_1(r\cos\theta, r\sin\theta)}^{u_2(r\cos\theta, r\sin\theta)} f(r\cos\theta, r\sin\theta, z) r dz dr d\theta \tag{4} \]
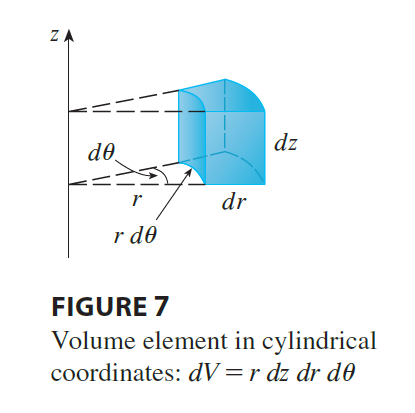
Formula 4 is the formula for triple integration in cylindrical coordinates. It says that we convert a triple integral from rectangular to cylindrical coordinates by writing \(x = r\cos\theta\), \(y = r\sin\theta\), leaving z as it is, using the appropriate limits of integration for z, r, and \(\theta\), and replacing dV by \(r dz dr d\theta\). (Figure 7 shows how to remember this.) It is worthwhile to use this formula when E is a solid region easily described in cylindrical coordinates, and especially when the function \(f(x, y, z)\) involves the expression \(x^2 + y^2\).
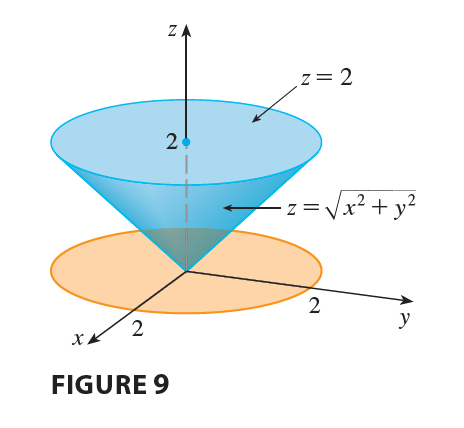
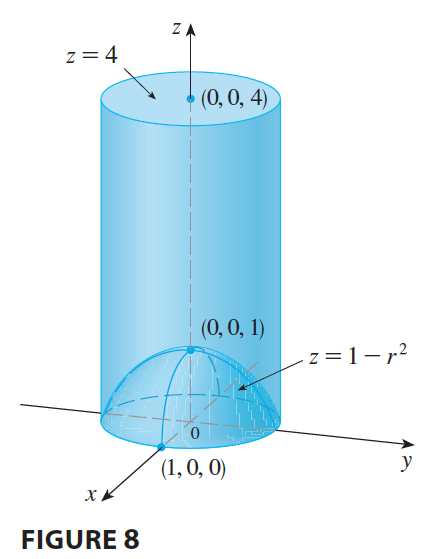
EXAMPLE 3 A solid E lies within the cylinder \(x^2 + y^2 = 1\), below the plane \(z=4\), and above the paraboloid \(z = 1 - x^2 - y^2\). (See Figure 8.) The density at any point is proportional to its distance from the axis of the cylinder. Find the mass of E.
EXAMPLE 4 Evaluate \(\int_{-2}^2 \int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} \int_{\sqrt{x^2+y^2}}^2 (x^2+y^2) dz dy dx\).
Exercise 1
Plot the point whose cylindrical coordinates are given. Then find the rectangular coordinates of the point. (a) \((4, \pi/3, -2)\) (b) \((2, -\pi/2, 1)\)
Exercise 2
Plot the point whose cylindrical coordinates are given. Then find the rectangular coordinates of the point. (a) \((\sqrt{2}, 3\pi/4, 2)\) (b) \((1, 1, 1)\)
Exercise 3
Change from rectangular to cylindrical coordinates. (a) \((-1, 1, 1)\) (b) \((-2, 2\sqrt{3}, 3)\)
Exercise 4
Change from rectangular to cylindrical coordinates. (a) \((-2, 2, 1)\) (b) \((2, 2, 2)\)
Exercise 5
Describe in words the surface whose equation is given. \(r=2\)
Exercise 6
Describe in words the surface whose equation is given. \(\theta = \pi/6\)
Exercise 7
Identify the surface whose equation is given. \(r^2 + z^2 = 4\)
Exercise 8
Identify the surface whose equation is given. \(r = 2\sin\theta\)
Exercise 9
Write the equations in cylindrical coordinates. (a) \(x^2 - x + y^2 + z^2 = 1\) (b) \(z = x^2 - y^2\)
Exercise 10
Write the equations in cylindrical coordinates. (a) \(2x^2 + 2y^2 - z^2 = 4\) (b) \(2xy + z = 1\)
Exercise 11
Sketch the solid described by the given inequalities. \(r^2 \le z \le 8 - r^2\)
Exercise 12
Sketch the solid described by the given inequalities. \(0 \le \theta \le \pi/2, r \le z \le 2\)
Exercise 13
A cylindrical shell is 20 cm long, with inner radius 6 cm and outer radius 7 cm. Write inequalities that describe the shell in an appropriate coordinate system. Explain how you have positioned the coordinate system with respect to the shell.
Exercise 14
Use a graphing device to draw the solid enclosed by the paraboloids \(z = x^2 + y^2\) and \(z = 5 - x^2 - y^2\).
Exercise 15
Sketch the solid whose volume is given by the integral and evaluate the integral. \[ \int_{-\pi/2}^{\pi/2} \int_0^2 \int_0^{r^2} r dz dr d\theta \]
Exercise 16
Sketch the solid whose volume is given by the integral and evaluate the integral. \[ \int_0^2 \int_0^{2\pi} \int_0^r r dz d\theta dr \]
Exercise 17
Use cylindrical coordinates. Evaluate \(\iiint_E \sqrt{x^2+y^2} dV\), where E is the region that lies inside the cylinder \(x^2+y^2=16\) and between the planes \(z=-5\) and \(z=4\).
Exercise 18
Use cylindrical coordinates. Evaluate \(\iiint_E z dV\), where E is enclosed by the paraboloid \(z = x^2+y^2\) and the plane \(z=4\).
Exercise 19
Use cylindrical coordinates. Evaluate \(\iiint_E (x+y+z) dV\), where E is the solid in the first octant that lies under the paraboloid \(z = 4 - x^2 - y^2\).
Exercise 20
Use cylindrical coordinates. Evaluate \(\iiint_E (x-y) dV\), where E is the solid that lies between the cylinders \(x^2+y^2=1\) and \(x^2+y^2=16\), above the xy-plane, and below the plane \(z=y+4\).
Exercise 21
Use cylindrical coordinates. Evaluate \(\iiint_E x^2 dV\), where E is the solid that lies within the cylinder \(x^2+y^2=1\), above the plane \(z=0\), and below the cone \(z^2 = 4x^2+4y^2\).
Exercise 22
Find the volume of the solid that lies within both the cylinder \(x^2+y^2=1\) and the sphere \(x^2+y^2+z^2=4\).
Exercise 23
Find the volume of the solid that is enclosed by the cone \(z=\sqrt{x^2+y^2}\) and the sphere \(x^2+y^2+z^2=2\).
Exercise 24
Find the volume of the solid that lies between the paraboloid \(z=x^2+y^2\) and the sphere \(x^2+y^2+z^2=2\).
Exercise 25
- Find the volume of the region E that lies between the paraboloid \(z=24-x^2-y^2\) and the cone \(z=2\sqrt{x^2+y^2}\).
- Find the centroid of E (the center of mass in the case where the density is constant).
Exercise 26
- Find the volume of the solid that the cylinder \(r=a\cos\theta\) cuts out of the sphere of radius a centered at the origin.
- Illustrate the solid of part (a) by graphing the sphere and the cylinder on the same screen.
Exercise 27
Find the mass and center of mass of the solid S bounded by the paraboloid \(z=4x^2+4y^2\) and the plane \(z=a\) (\(a>0\)) if S has constant density K.
Exercise 28
Find the mass of a ball B given by \(x^2+y^2+z^2 \le a^2\) if the density at any point is proportional to its distance from the z-axis.
Exercise 29
Evaluate the integral by changing to cylindrical coordinates. \[ \int_{-3}^3 \int_0^{\sqrt{9-x^2}} \int_0^{9-x^2-y^2} \sqrt{x^2+y^2} dz dy dx \]
Exercise 30
Evaluate the integral by changing to cylindrical coordinates. \[ \int_0^1 \int_0^{\sqrt{1-y^2}} \int_{x^2+y^2}^{\sqrt{x^2+y^2}} xz \ dz \ dx \ dy \]
Exercise 31
When studying the formation of mountain ranges, geologists estimate the amount of work required to lift a mountain from sea level. Consider a mountain that is essentially in the shape of a right circular cone. Suppose that the weight density of the material in the vicinity of a point P is \(g(P)\) and the height is \(h(P)\). (a) Find a definite integral that represents the total work done in forming the mountain. (b) Assume that Mount Fuji in Japan is in the shape of a right circular cone with radius 62,000 ft, height 12,400 ft, and density a constant 200 lb/ft\(^3\). How much work was done in forming Mount Fuji if the land was initially at sea level?