Section 15.8: Triple Integration in Spherical Coordinates
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 15.8: Triple Integration in Spherical Coordinates |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 3:57 AM |
Table of contents
- Spherical Coordinates
- Relationship between Spherical and Rectangular coordinates
- Triple Integrals with Spherical Coordinates
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
- Exercise 44
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
- Exercise 49
Spherical Coordinates
Another useful coordinate system in three dimensions is the spherical coordinate system. It simplifies the evaluation of triple integrals over regions bounded by spheres or cones.
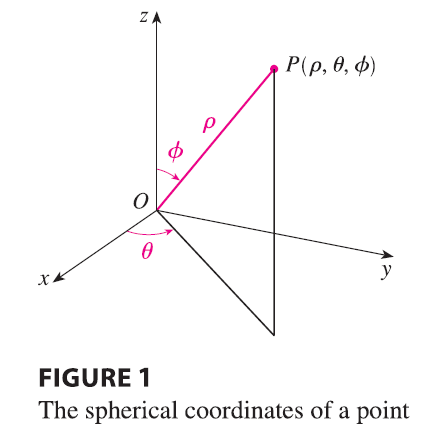
The spherical coordinates \((\rho, \theta, \phi)\) of a point P in space are shown in Figure 1, where \(\rho = |OP|\) is the distance from the origin to P, \(\theta\) is the same angle as in cylindrical coordinates, and \(\phi\) is the angle between the positive z-axis and the line segment OP. Note that \[ \rho \ge 0 \qquad 0 \le \phi \le \pi \]
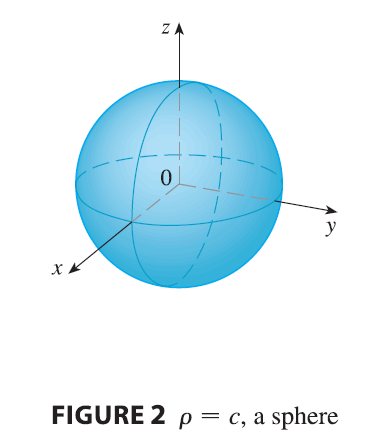
The spherical coordinate system is especially useful in problems where there is symmetry about a point, and the origin is placed at this point. For example, the sphere with center the origin and radius c has the simple equation \(\rho = c\) (see Figure 2); this is the reason for the name “spherical” coordinates.
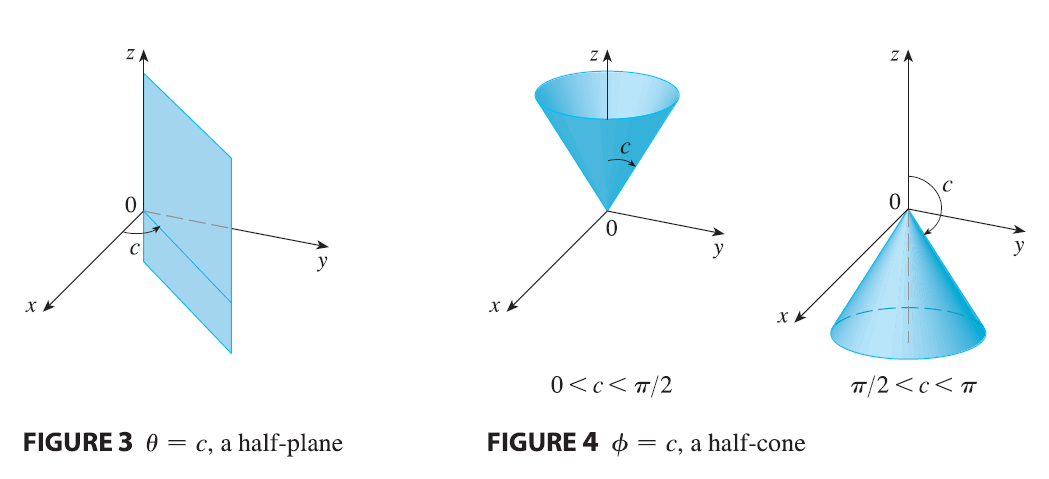
The graph of the equation \(\theta = c\) is a vertical half-plane (see Figure 3), and the equation \(\phi = c\) represents a half-cone with the z-axis as its axis (see Figure 4).
Relationship between Spherical and Rectangular coordinates
The relationship between rectangular and spherical coordinates can be seen from Figure 5.
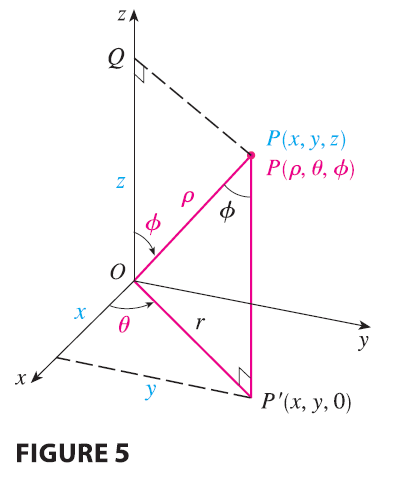
From triangles OPQ and OPP’ we have \[ z = \rho \cos \phi \qquad r = \rho \sin \phi \] But \(x = r \cos \theta\) and \(y = r \sin \theta\), so to convert from spherical to rectangular coordinates, we use the equations
\[ x = \rho \sin \phi \cos \theta \qquad y = \rho \sin \phi \sin \theta \qquad z = \rho \cos \phi \tag{1} \]
Also, the distance formula shows that
\[ \rho^2 = x^2 + y^2 + z^2 \tag{2} \]
We use this equation in converting from rectangular to spherical coordinates.
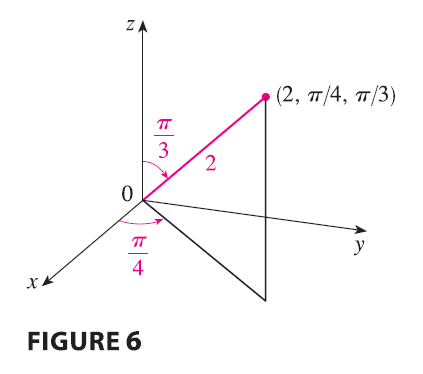
EXAMPLE 1 The point \((2, \pi/4, \pi/3)\) is given in spherical coordinates. Plot the point and find its rectangular coordinates.
EXAMPLE 2 The point \((0, 2\sqrt{3}, -2)\) is given in rectangular coordinates. Find spherical coordinates for this point.
Triple Integrals with Spherical Coordinates
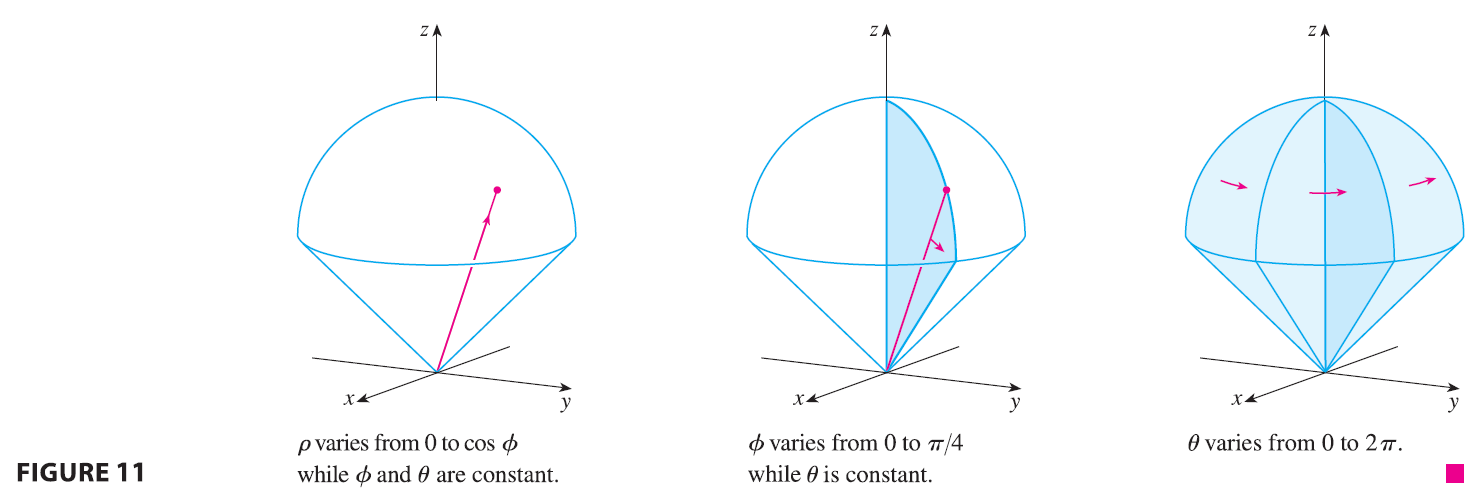
In the spherical coordinate system the counterpart of a rectangular box is a spherical wedge \[ E = \{(\rho, \theta, \phi) | a \le \rho \le b, \alpha \le \theta \le \beta, c \le \phi \le d\} \] where \(a \ge 0\) and \(\beta - \alpha \le 2\pi\), and \(d-c \le \pi\). Although we defined triple integrals by dividing solids into small boxes, it can be shown that dividing a solid into small spherical wedges always gives the same result. So we divide E into smaller spherical wedges \(E_{ijk}\) by means of equally spaced spheres \(\rho = \rho_i\), half-planes \(\theta = \theta_j\), and half-cones \(\phi = \phi_k\).
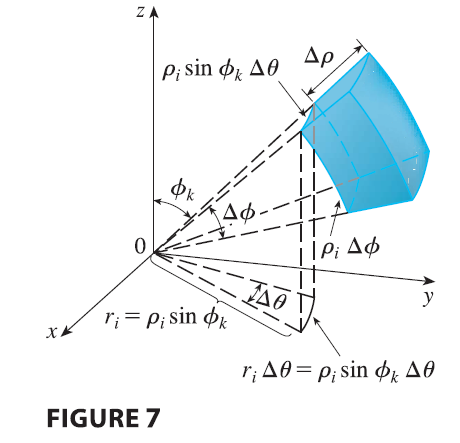
Figure 7 shows that \(E_{ijk}\) is approximately a rectangular box with dimensions \(\Delta\rho\), \(\rho_i \Delta\phi\) (arc of a circle with radius \(\rho_i\), angle \(\Delta\phi\)), and \(\rho_i \sin\phi_k \Delta\theta\) (arc of a circle with radius \(\rho_i \sin\phi_k\), angle \(\Delta\theta\)). So an approximation to the volume of \(E_{ijk}\) is given by \[ \Delta V_{ijk} \approx (\Delta\rho)(\rho_i \Delta\phi)(\rho_i \sin\phi_k \Delta\theta) = \rho_i^2 \sin\phi_k \Delta\rho \Delta\theta \Delta\phi \] In fact, it can be shown, with the aid of the Mean Value Theorem (Exercise 49), that the volume of \(E_{ijk}\) is given exactly by \[ \Delta V_{ijk} = \tilde{\rho_i}^2 \sin\tilde{\phi_k} \Delta\rho \Delta\theta \Delta\phi \] where \((\tilde{\rho_i}, \tilde{\theta_j}, \tilde{\phi_k})\) is some point in \(E_{ijk}\). Let \((x_{ijk}, y_{ijk}, z_{ijk})\) be the rectangular coordinates of this point. Then \[ \iiint_E f(x, y, z) dV = \lim_{l,m,n \to \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(x_{ijk}, y_{ijk}, z_{ijk}) \Delta V_{ijk} \] \[ = \lim_{l,m,n \to \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(\tilde{\rho_i}\sin\tilde{\phi_k}\cos\tilde{\theta_j}, \tilde{\rho_i}\sin\tilde{\phi_k}\sin\tilde{\theta_j}, \tilde{\rho_i}\cos\tilde{\phi_k}) \tilde{\rho_i}^2 \sin\tilde{\phi_k} \Delta\rho \Delta\theta \Delta\phi \] But this sum is a Riemann sum for the function \[ F(\rho, \theta, \phi) = f(\rho\sin\phi\cos\theta, \rho\sin\phi\sin\theta, \rho\cos\phi)\rho^2\sin\phi \]
Consequently, we have arrived at the following formula for triple integration in spherical coordinates. \[ \iiint_E f(x, y, z) dV = \int_c^d \int_\alpha^\beta \int_a^b f(\rho\sin\phi\cos\theta, \rho\sin\phi\sin\theta, \rho\cos\phi)\rho^2\sin\phi d\rho d\theta d\phi \tag{3} \] where E is a spherical wedge given by \[ E = \{(\rho, \theta, \phi) | a \le \rho \le b, \alpha \le \theta \le \beta, c \le \phi \le d\} \]
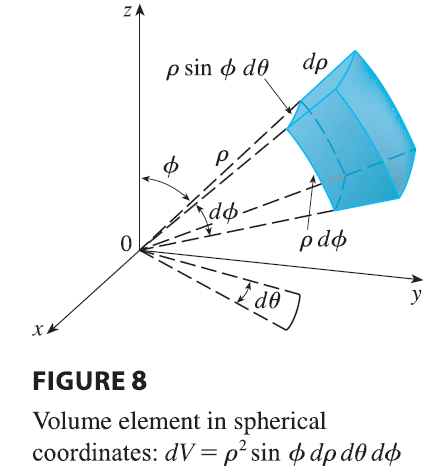
Formula 3 says that we convert a triple integral from rectangular coordinates to spherical coordinates by writing \[ x = \rho\sin\phi\cos\theta \qquad y = \rho\sin\phi\sin\theta \qquad z = \rho\cos\phi \] using the appropriate limits of integration, and replacing dV by \(\rho^2\sin\phi d\rho d\theta d\phi\). This is illustrated in Figure 8.
This formula can be extended to include more general spherical regions such as \[ E = \{(\rho, \theta, \phi) | \alpha \le \theta \le \beta, c \le \phi \le d, g_1(\theta, \phi) \le \rho \le g_2(\theta, \phi)\} \] In this case the formula is the same as in (3) except that the limits of integration for \(\rho\) are \(g_1(\theta, \phi)\) and \(g_2(\theta, \phi)\). Usually, spherical coordinates are used in triple integrals when surfaces such as cones and spheres form the boundary of the region of integration.
EXAMPLE 3 Evaluate \(\iiint_B e^{(x^2+y^2+z^2)^{3/2}} dV\), where B is the unit ball: \[ B = \{(x, y, z) | x^2+y^2+z^2 \le 1\} \]
EXAMPLE 4 Use spherical coordinates to find the volume of the solid that lies above the cone \(z = \sqrt{x^2+y^2}\) and below the sphere \(x^2+y^2+z^2=z\). (See Figure 9.)
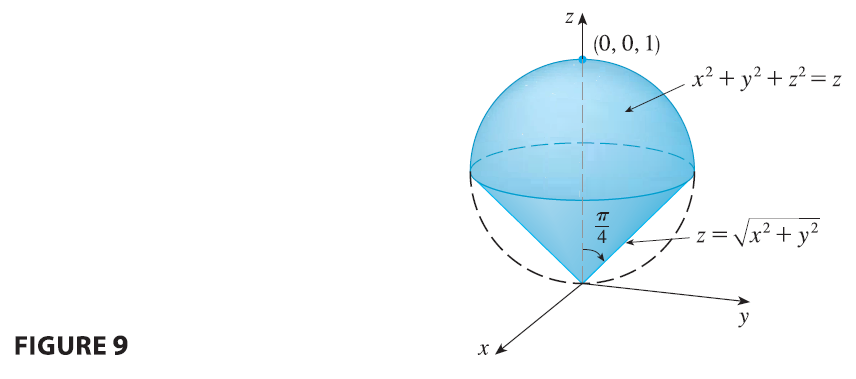
Exercise 1
Plot the point whose spherical coordinates are given. Then find the rectangular coordinates of the point. (a) \((6, \pi/3, \pi/6)\) (b) \((3, \pi/2, 3\pi/4)\)
Exercise 2
Plot the point whose spherical coordinates are given. Then find the rectangular coordinates of the point. (a) \((2, \pi/2, \pi/2)\) (b) \((4, -\pi/4, \pi/3)\)
Exercise 3
Change from rectangular to spherical coordinates. (a) \((0, -2, 0)\) (b) \((-1, 1, -\sqrt{2})\)
Exercise 4
Change from rectangular to spherical coordinates. (a) \((1, 0, \sqrt{3})\) (b) \((\sqrt{3}, -1, 2\sqrt{3})\)
Exercise 5
Describe in words the surface whose equation is given. \(\phi = \pi/3\)
Exercise 6
Describe in words the surface whose equation is given. \(\rho^2 - 3\rho + 2 = 0\)
Exercise 7
Identify the surface whose equation is given. \(\rho\cos\phi = 1\)
Exercise 8
Identify the surface whose equation is given. \(\rho = \cos\phi\)
Exercise 9
Write the equation in spherical coordinates. (a) \(x^2+y^2+z^2 = 9\) (b) \(x^2-y^2-z^2 = 1\)
Exercise 10
Write the equation in spherical coordinates. (a) \(z = x^2+y^2\) (b) \(z = x^2-y^2\)
Exercise 11
Sketch the solid described by the given inequalities. \(\rho \le 1, 0 \le \phi \le \pi/6, 0 \le \theta \le \pi\)
Exercise 12
Sketch the solid described by the given inequalities. \(1 \le \rho \le 2, \pi/2 \le \phi \le \pi\)
Exercise 13
Sketch the solid described by the given inequalities. \(2 \le \rho \le 4, 0 \le \phi \le \pi/3, 0 \le \theta \le \pi\)
Exercise 14
Sketch the solid described by the given inequalities. \(\rho \le 2, \rho \le \csc\phi\)
Exercise 15
A solid lies above the cone \(z = \sqrt{x^2+y^2}\) and below the sphere \(x^2+y^2+z^2=z\). Write a description of the solid in terms of inequalities involving spherical coordinates.
Exercise 16
- Find inequalities that describe a hollow ball with diameter 30 cm and thickness 0.5 cm. Explain how you have positioned the coordinate system that you have chosen.
- Suppose the ball is cut in half. Write inequalities that describe one of the halves.
Exercise 17
Sketch the solid whose volume is given by the integral and evaluate the integral. \[ \int_0^{\pi/6} \int_0^{\pi/2} \int_0^3 \rho^2 \sin\phi \, d\rho \, d\theta \, d\phi \]
Exercise 18
Sketch the solid whose volume is given by the integral and evaluate the integral. \[ \int_0^{\pi/4} \int_0^{2\pi} \int_0^{\sec\phi} \rho^2 \sin\phi \, d\rho \, d\theta \, d\phi \]
Exercise 19
Set up the triple integral of an arbitrary continuous function \(f(x, y, z)\) in cylindrical or spherical coordinates over the solid shown.
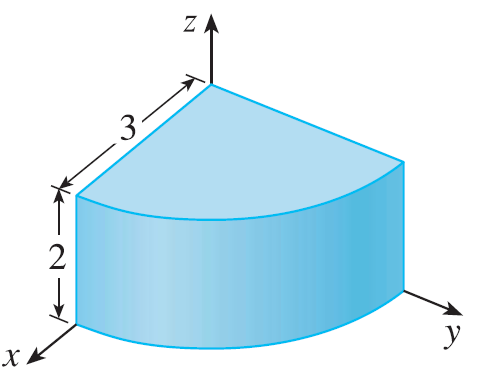
Exercise 20
Set up the triple integral of an arbitrary continuous function \(f(x, y, z)\) in cylindrical or spherical coordinates over the solid shown.
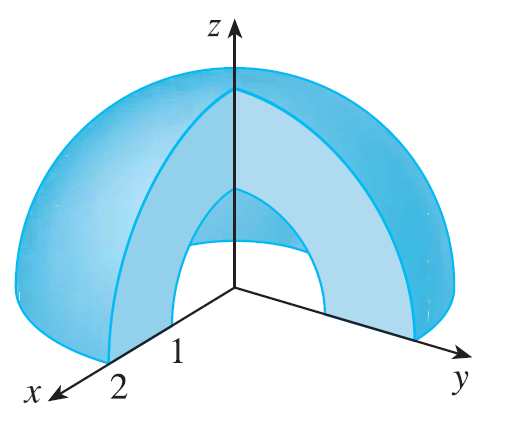
Exercise 21
Use spherical coordinates. Evaluate \(\iiint_B (x^2+y^2+z^2)^2 dV\), where B is the ball with center the origin and radius 5.
Exercise 22
Use spherical coordinates. Evaluate \(\iiint_E y^2z^2 dV\), where E lies above the cone \(\phi = \pi/3\) and below the sphere \(\rho=1\).
Exercise 23
Use spherical coordinates. Evaluate \(\iiint_E (x^2+y^2) dV\), where E lies between the spheres \(x^2+y^2+z^2=4\) and \(x^2+y^2+z^2=9\).
Exercise 24
Use spherical coordinates. Evaluate \(\iiint_E y^2 dV\), where E is the solid hemisphere \(x^2+y^2+z^2 \le 9, y \ge 0\).
Exercise 25
Use spherical coordinates. Evaluate \(\iiint_E xe^{x^2+y^2+z^2} dV\), where E is the portion of the unit ball \(x^2+y^2+z^2 \le 1\) that lies in the first octant.
Exercise 26
Use spherical coordinates. Evaluate \(\iiint_E \sqrt{x^2+y^2+z^2} dV\), where E lies above the cone \(z=\sqrt{x^2+y^2}\) and between the spheres \(x^2+y^2+z^2=1\) and \(x^2+y^2+z^2=4\).
Exercise 27
Find the volume of the part of the ball \(\rho \le a\) that lies between the cones \(\phi = \pi/6\) and \(\phi = \pi/3\).
Exercise 28
Find the average distance from a point in a ball of radius a to its center.
Exercise 29
- Find the volume of the solid that lies above the cone \(\phi = \pi/3\) and below the sphere \(\rho = 4\cos\phi\).
- Find the centroid of the solid in part (a).
Exercise 30
Find the volume of the solid that lies within the sphere \(x^2+y^2+z^2=4\), above the xy-plane, and below the cone \(z=\sqrt{x^2+y^2}\).
Exercise 31
- Find the centroid of the solid in Example 4. (Assume constant density K.)
- Find the moment of inertia about the z-axis for this solid.
Exercise 32
Let H be a solid hemisphere of radius a whose density at any point is proportional to its distance from the center of the base. (a) Find the mass of H. (b) Find the center of mass of H. (c) Find the moment of inertia of H about its axis.
Exercise 33
- Find the centroid of a solid homogeneous hemisphere of radius a.
- Find the moment of inertia of the solid in part (a) about a diameter of its base.
Exercise 34
Find the mass and center of mass of a solid hemisphere of radius a if the density at any point is proportional to its distance from the base.
Exercise 35
Use cylindrical or spherical coordinates, whichever seems more appropriate. Find the volume and centroid of the solid E that lies above the cone \(z=\sqrt{x^2+y^2}\) and below the sphere \(x^2+y^2+z^2=1\).
Exercise 36
Use cylindrical or spherical coordinates, whichever seems more appropriate. Find the volume of the smaller wedge cut from a sphere of radius a by two planes that intersect along a diameter at an angle of \(\pi/6\).
Exercise 37
Use cylindrical or spherical coordinates, whichever seems more appropriate. A solid cylinder with constant density has base radius a and height h. (a) Find the moment of inertia of the cylinder about its axis. (b) Find the moment of inertia of the cylinder about a diameter of its base.
Exercise 38
Use cylindrical or spherical coordinates, whichever seems more appropriate. A solid right circular cone with constant density has base radius a and height h. (a) Find the moment of inertia of the cone about its axis. (b) Find the moment of inertia of the cone about a diameter of its base.
Exercise 39
Evaluate \(\iiint_E z \, dV\), where E lies above the paraboloid \(z=x^2+y^2\) and below the plane \(z=2y\). Use either the Table of Integrals (on Reference Pages 6-10) or a computer algebra system to evaluate the integral.
Exercise 40
- Find the volume enclosed by the torus \(\rho = \sin\phi\).
- Use a computer to draw the torus.
Exercise 41
Evaluate the integral by changing to spherical coordinates. \[ \int_0^1 \int_0^{\sqrt{1-x^2}} \int_{\sqrt{x^2+y^2}}^{\sqrt{2-x^2-y^2}} xy \, dz \, dy \, dx \]
Exercise 42
Evaluate the integral by changing to spherical coordinates. \[ \int_{-a}^a \int_{-\sqrt{a^2-y^2}}^{\sqrt{a^2-y^2}} \int_{-\sqrt{a^2-x^2-y^2}}^{\sqrt{a^2-x^2-y^2}} (x^2z + y^2z + z^3) \, dz \, dx \, dy \]
Exercise 43
Evaluate the integral by changing to spherical coordinates. \[ \int_{-2}^2 \int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} \int_{2-\sqrt{4-x^2-y^2}}^{2+\sqrt{4-x^2-y^2}} (x^2+y^2+z^2)^{3/2} \, dz \, dy \, dx \]
Exercise 44
A model for the density \(\delta\) of the earth’s atmosphere near its surface is \[ \delta = 619.09 - 0.000097\rho \] where \(\rho\) (the distance from the center of the earth) is measured in meters and \(\delta\) is measured in kilograms per cubic meter. If we take the surface of the earth to be a sphere with radius 6370 km, then this model is a reasonable one for \(6.370 \times 10^6 \le \rho \le 6.375 \times 10^6\). Use this model to estimate the mass of the atmosphere between the ground and an altitude of 5 km.
Exercise 45
Use a graphing device to draw a silo consisting of a cylinder with radius 3 and height 10 surmounted by a hemisphere.
Exercise 46
The latitude and longitude of a point P in the Northern Hemisphere are related to spherical coordinates \(\rho, \theta, \phi\) as follows. We take the origin to be the center of the earth and the positive z-axis to pass through the North Pole. The positive x-axis passes through the point where the prime meridian (the meridian through Greenwich, England) intersects the equator. Then the latitude of P is \(\alpha = 90^\circ - \phi^\circ\) and the longitude is \(\beta = 360^\circ - \theta^\circ\). Find the great-circle distance from Los Angeles (lat. 34.06 N, long. 118.25 W) to Montreal (lat. 45.50 N, long. 73.60 W). Take the radius of the earth to be 3960 mi. (A great circle is the circle of intersection of a sphere and a plane through the center of the sphere.)
Exercise 47
The surfaces \(\rho = 1 + \frac{1}{5}\sin(m\theta)\sin(n\phi)\) have been used as models for tumors. The “bumpy sphere” with \(m=6\) and \(n=5\) is shown. Use a computer algebra system to find the volume it encloses.
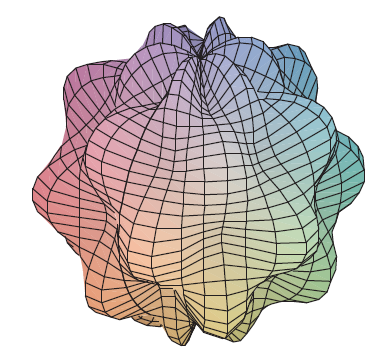
Exercise 48
Show that \[ \int_{-\infty}^\infty \int_{-\infty}^\infty \int_{-\infty}^\infty \sqrt{x^2+y^2+z^2} e^{-(x^2+y^2+z^2)} \, dx \, dy \, dz = 2\pi \] (The improper triple integral is defined as the limit of a triple integral over a solid sphere as the radius of the sphere increases indefinitely.)
Exercise 49
- Use cylindrical coordinates to show that the volume of the solid bounded above by the sphere \(r^2+z^2=a^2\) and below by the cone \(z=r\cot\phi_0\) (or \(\phi=\phi_0\)), where \(0 < \phi_0 < \pi/2\), is \[ V = \frac{2\pi a^3}{3}(1-\cos\phi_0) \]
- Deduce a that the volume of the spherical wedge given by \(\rho_1 \le \rho \le \rho_2, \theta_1 \le \theta \le \theta_2, \phi_1 \le \phi \le \phi_2\) is \[ \Delta V = \frac{\rho_2^3 - \rho_1^3}{3}(\cos\phi_1 - \cos\phi_2)(\theta_2 - \theta_1). \]
- Use the Mean Value Theorem to show that the volume in part (b) can be written as \[ \Delta V = \tilde{\rho}^2 \sin\tilde{\phi} \, \Delta\rho \, \Delta\theta \, \Delta\phi \] where \(\tilde{\rho}\) lies between \(\rho_1\) and \(\rho_2\), \(\tilde{\phi}\) lies between \(\phi_1\) and \(\phi_2\), \(\Delta\rho = \rho_2 - \rho_1\), \(\Delta\theta = \theta_2 - \theta_1\), and \(\Delta\phi = \phi_2 - \phi_1\).