Section 1.3: Functions
| Site: | Freebirds Moodle |
| Course: | NCERT XIIth Mathematics |
| Book: | Section 1.3: Functions |
| Printed by: | Guest user |
| Date: | Monday, 18 August 2025, 8:44 PM |
Types of Functions
Consider the functions \(f_1, f_2, f_3\) and \(f_4\) given by the following diagrams.
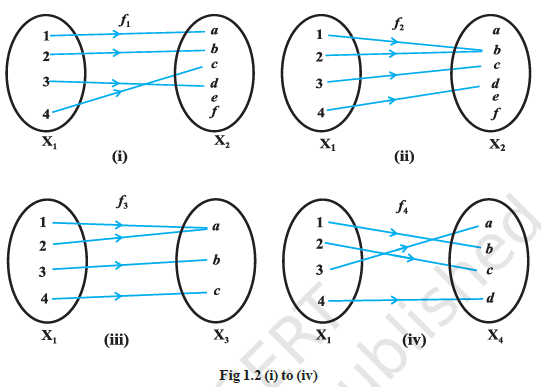
In Fig 1.2, we observe that the images of distinct elements of \(X_1\) under the function \(f_1\) are distinct, but the image of two distinct elements 1 and 2 of \(X_1\) under \(f_1\) is same, namely \(b\). Further, there are some elements like \(e\) and \(f\) in \(X_2\) which are not images of any element of \(X_1\) under \(f_1\), while all elements of \(X_3\) are images of some elements of \(X_1\) under \(f_3\). The above observations lead to the following definitions:
Definition: Injdective Functions or One-One
Functions
A function \(f : X \to Y\) is defined
to be one-one (or injective), if the
images of distinct elements of \(X\)
under \(f\) are distinct, i.e. for
every \(x_1, x_2 \in X\), \(f(x_1) = f(x_2)\) implies \(x_1 = x_2\). Otherwise, \(f\) is called many-one.
The functions \(f_1\) and \(f_4\) in Fig 1.2 (i) and (iv) are one-one and the function \(f_2\) and \(f_3\) in Fig 1.2 (ii) and (iii) are many-one.
Definition: Onto Functions or Surjective
Functions
A function \(f : X \to Y\) is said to
be onto (or surjective), if every
element of \(Y\) is the image of some
element of \(X\) under \(f\), i.e., for every \(y \in Y\), there exists an element \(x\) in \(X\) such that \(f(x) = y\).
The function \(f_3\) and \(f_4\) in Fig 1.2 (iii), (iv) are onto and the function \(f_1\) in Fig 1.2 (i) is not onto as elements \(e, f\) in \(X_2\) are not the image of any element in \(X_1\) under \(f_1\).
Remark
\(f : X \to Y\) is onto if and only if
\(\text{Range of } f = Y\).
Definition: Bijective functions
A function \(f : X \to Y\) is said to
be one-one and onto (or bijective), if \(f\) is both one-one and onto.
The function \(f_4\) in Fig 1.2 (iv) is one-one and onto.
Example Exercise
Example 7
Let \(A\) be the set of all 50 students
of Class X in a school. Let \(f : A \to
\mathbb{N}\) be function defined by \(f(x) = \text{roll number of the student }
x\). Show that \(f\) is one-one
but not onto.
Example exercise
Example 8
Show that the function \(f : \mathbb{N} \to
\mathbb{N}\), given by \(f(x) =
2x\), is one-one but not onto.
Example Exercise
Example 9
Prove that the function \(f : \mathbb{R} \to
\mathbb{R}\), given by \(f(x) =
2x\), is one-one and onto.
Example Exercise
Example 10
Show that the function \(f : \mathbb{N} \to
\mathbb{N}\) given by \(f(1) = f(2) =
1\) and \(f(x) = x - 1\), for
every \(x > 2\), is onto but not
one-one.
Example Exercise
Example 11
Show that the function \(f : \mathbb{R} \to
\mathbb{R}\), defined as \(f(x) =
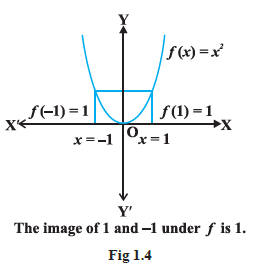
x^2\), is neither one-one nor onto.
Example Exercise
Example 12
Show that \(f : \mathbb{N} \to
\mathbb{N}\), given by
\[
f(x) =
\begin{cases}
x + 1, & \text{if } x \text{ is odd} \\
x - 1, & \text{if } x \text{ is even}
\end{cases}
\]
is both one-one and onto.
Example Exercise
Example 13
Show that an onto function \(f : \{1, 2, 3\}
\to \{1, 2, 3\}\) is always one-one.
Example Exercise
Example 14
Show that a one-one function \(f : \{1, 2, 3\}
\to \{1, 2, 3\}\) must be onto.
Exercise
Show that the function \(f : \mathbb{R} \to
\mathbb{R}\), defined by \(f(x) =
\frac{1}{x}\) is one-one and onto,
where \(\mathbb{R}\) is the set of all
non-zero real numbers. Is the result true, if the domain \(\mathbb{R}\) is replaced by \(\mathbb{N}\) with co-domain being same as
\(\mathbb{R}\)?
Exercise 2
Check the injectivity and surjectivity of the following functions:
- \(f : \mathbb{N} \to \mathbb{N}\)
given by \(f(x) = x^2\)
- \(f : \mathbb{Z} \to \mathbb{Z}\)
given by \(f(x) = x^2\)
- \(f : \mathbb{R} \to \mathbb{R}\)
given by \(f(x) = x^2\)
- \(f : \mathbb{N} \to \mathbb{N}\)
given by \(f(x) = x^3\)
- \(f : \mathbb{Z} \to \mathbb{Z}\) given by \(f(x) = x^3\)
Exercise 3
Prove that the Greatest Integer Function \(f : \mathbb{R} \to \mathbb{R}\), given by
\(f(x) = [x]\), is neither one-one nor
onto,
where \([x]\) denotes the greatest
integer less than or equal to \(x\).
Exercise 4
Show that the Modulus Function \(f :
\mathbb{R} \to \mathbb{R}\), given by \(f(x) = |x|\), is neither one-one nor
onto,
where \(|x|\) is \(x\), if \(x\) is positive or 0 and \(|x| = -x\), if \(x\) is negative.
Exercise 5
Show that the Signum Function \(f :
\mathbb{R} \to \mathbb{R}\), given by
\[
f(x) =
\begin{cases}
1, & \text{if } x > 0 \\
0, & \text{if } x = 0 \\
-1, & \text{if } x < 0
\end{cases}
\] is neither one-one nor onto.
Exercise 6
Let \(A = \{1, 2, 3\}, B = \{4, 5, 6, 7\}\) and let \(f = \{(1, 4), (2, 5), (3, 6)\}\) be a function from \(A\) to \(B\). Show that \(f\) is one-one.
Exercise 7
In each of the following cases, state whether the function is
one-one, onto or bijective. Justify your answer.
(i) \(f : \mathbb{R} \to \mathbb{R}\)
defined by \(f(x) = 3 - 4x\)
(ii) \(f : \mathbb{R} \to \mathbb{R}\)
defined by \(f(x) = 1 + x^2\)
Exercise 8
Let \(A\) and \(B\) be sets. Show that \(f : A \times B \to B \times A\) such that \(f(a, b) = (b, a)\) is a bijective function.
Exercise 9
Let \(f : \mathbb{N} \to
\mathbb{N}\) be defined by
\[
f(n) =
\begin{cases}
\frac{n+1}{2}, & \text{if } n \text{ is odd} \\
\frac{n}{2}, & \text{if } n \text{ is even}
\end{cases}
\] for all \(n \in
\mathbb{N}\).
State whether the function \(f\) is
bijective. Justify your answer.
Exercise 10
Let \(A = \mathbb{R} - \{3\}\) and
\(B = \mathbb{R} - \{1\}\). Consider
the function \(f : A \to B\) defined
by
\[
f(x) = \frac{x - 2}{x - 3}
\] Is \(f\) one-one and
onto? Justify your answer.
Exercise 11
Let \(f : \mathbb{R} \to
\mathbb{R}\) be defined as \(f(x) =
x^4\). Choose the correct answer.
(A) \(f\) is one-one onto
(B) \(f\) is many-one onto
(C) \(f\) is one-one but not onto
(D) \(f\) is neither one-one nor
onto