Inverse Trigonometric Functions
| Site: | Freebirds Moodle |
| Course: | NCERT XIIth Mathematics |
| Book: | Inverse Trigonometric Functions |
| Printed by: | Guest user |
| Date: | Monday, 18 August 2025, 8:44 PM |
Table of contents
- Chapter 2
- 2.1 Introduction
- 2.2 Basic Concepts
- Sin Function and Its Domain Restrictions
- Remarks
- Sin Graph
- cos Function and Its Domain Restrictions
- Cos Graph
- Cos Function and Its Domain Restrictions
- Cosec Graph
- Sec Function and Its Domain Restrictions
- Sec Graph
- tan Function and Its Domain Restrictions
- tan Graph
- Cot Function and Its Domain Restrictions
- Cot Graph
- domains and ranges
- Note
- Example 1
- Example 2
- 2.3 Properties of Inverse Trigonometric Functions
- Example 3
- Example 4
- Example 5
- Miscellaneous Examples
- Summary
- Historical Note
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 23
- Exercise 24
- Exercise 25
- Exercise 26
- Exercise 27
- Exercise 28
- Exercise 29
- Exercise 30
- Exercise 31
- Exercise 32
- Exercise 33
- Exercise 34
- Exercise 35
- Exercise 36
- Exercise 37
- Exercise 38
- Exercise 39
- Exercise 40
- Exercise 41
- Exercise 42
- Exercise 43
Chapter 2
INVERSE TRIGONOMETRIC FUNCTIONS > Mathematics, in general, is fundamentally the science of > self-evident things. > — FELIX KLEIN >
2.1 Introduction
In Chapter 1, we have studied that the inverse of a function f, denoted by \(f^{-1}\), exists if f is one-one and onto. There are many functions which are not one-one, onto or both and hence we can not talk of their inverses. In Class XI, we studied that trigonometric functions are not one-one and onto over their natural domains and ranges and hence their inverses do not exist. In this chapter, we shall study about the restrictions on domains and ranges of trigonometric functions which ensure the existence of their inverses and observe their behaviour through graphical representations. Besides, some elementary properties will also be discussed.
Aryabhata (476-550 A.D.)
The inverse trigonometric functions play an important role in calculus for they serve to define many integrals. The concepts of inverse trigonometric functions is also used in science and engineering.
2.2 Basic Concepts
In Class XI, we have studied trigonometric functions, which are defined as follows: sine function, i.e., sine: \(R \rightarrow [-1, 1]\) cosine function, i.e., cos: \(R \rightarrow [-1, 1]\) tangent function, i.e., tan: \(R - \{x: x = (2n+1)\frac{\pi}{2}, n \in Z\} \rightarrow R\) cotangent function, i.e., cot: \(R - \{x: x = n\pi, n \in Z\} \rightarrow R\) secant function, i.e., sec: \(R - \{x: x = (2n+1)\frac{\pi}{2}, n \in Z\} \rightarrow R - (-1, 1)\) cosecant function, i.e., cosec: \(R - \{x: x = n\pi, n \in Z\} \rightarrow R - (-1, 1)\)
Sin Function and Its Domain Restrictions
We have also learnt in Chapter 1 that if f: X→Y such that \(f(x)=y\) is one-one and onto, then we can define a unique function \(g: Y \rightarrow X\) such that \(g(y)=x\), where \(x \in X\) and \(y=f(x)\), \(y \in Y\). Here, the domain of g = range of f and the range of g = domain of f. The function g is called the inverse of f and is denoted by \(f^{-1}\). Further, g is also one-one and onto and inverse of g is f. Thus, \(g^{-1} = (f^{-1})^{-1} = f\). We also have \((f^{-1} \circ f)(x) = f^{-1}(f(x)) = f^{-1}(y) = x\) and \((f \circ f^{-1})(y) = f(f^{-1}(y)) = f(x) = y\).
Since the domain of sine function is the set of all real numbers and range is the closed interval [-1, 1]. If we restrict its domain to \([\frac{-\pi}{2}, \frac{\pi}{2}]\) then it becomes one-one and onto with range [-1, 1]. Actually, sine function restricted to any of the intervals \([\frac{-3\pi}{2}, \frac{-\pi}{2}], [\frac{-\pi}{2}, \frac{\pi}{2}], [\frac{\pi}{2}, \frac{3\pi}{2}]\) etc., is one-one and its range is [-1, 1]. We can, therefore, define the inverse of sine function in each of these intervals. We denote the inverse of sine function by \(sin^{-1}\) (arc sine function). Thus, \(sin^{-1}\) is a function whose domain is [-1, 1] and range could be any of the intervals \([\frac{-3\pi}{2}, \frac{-\pi}{2}], [\frac{-\pi}{2}, \frac{\pi}{2}]\) or \([\frac{\pi}{2}, \frac{3\pi}{2}]\) and so on. Corresponding to each such interval, we get a branch of the function \(sin^{-1}\). The branch with range \([\frac{-\pi}{2}, \frac{\pi}{2}]\) is called the principal value branch, whereas other intervals as range give different branches of \(sin^{-1}\). When we refer to the function \(sin^{-1}\), we take it as the function whose domain is [-1, 1] and range is \([\frac{-\pi}{2}, \frac{\pi}{2}]\). We write \(sin^{-1}: [-1, 1] \rightarrow [\frac{-\pi}{2}, \frac{\pi}{2}]\) From the definition of the inverse functions, it follows that sin\((sin^{-1}x) = x\) if \(-1 \le x \le 1\) and \(sin^{-1}(sin x) = x\) if \(-\frac{\pi}{2} \le x \le \frac{\pi}{2}\). In other words, if \(y = sin^{-1}x\), then sin \(y = x\).
Remarks
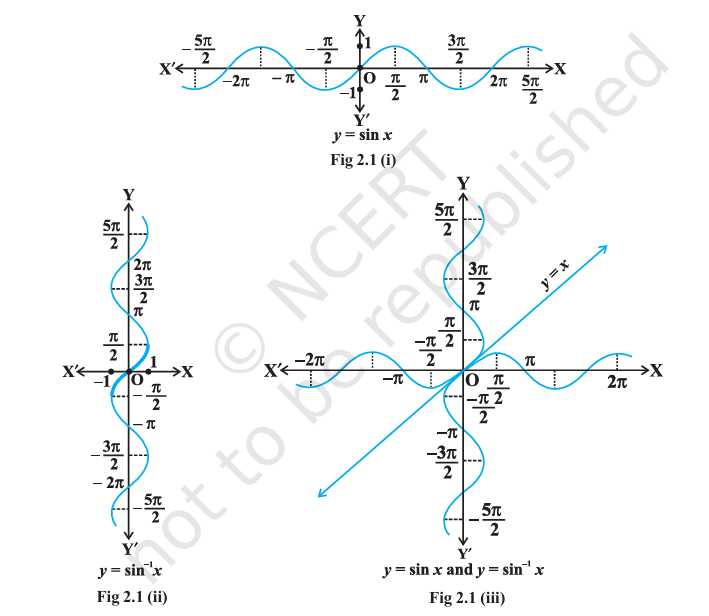
- We know from Chapter 1, that if \(y=f(x)\) is an invertible function, then \(x = f^{-1}(y)\). Thus, the graph of \(sin^{-1}\) function can be obtained from the graph of original function by interchanging x and y axes, i.e., if \((a, b)\) is a point on the graph of sine function, then \((b, a)\) becomes the corresponding point on the graph of inverse of sine function of sine function. Thus, the graph of the function \(y = sin^{-1}x\) can be obtained from the graph of \(y = sin x\) by interchanging x and y axes. The graphs of \(y = sin x\) and \(y = sin^{-1}x\) are as given in Fig 2.1 (i), (ii), (iii). The dark portion of the graph of \(y = sin^{-1}x\) represent the principal value branch.
Sin Graph
- It can be shown that the graph of an inverse function can be
obtained from the corresponding graph of original function as a mirror
image (i.e., reflection) along the line \(y=x\). This can be visualised by looking
the graphs of \(y=sin~x\) and \(y=sin^{-1}x\) as given in the same axes
(Fig 2.1 (iii)).
cos Function and Its Domain Restrictions
Like sine function, the cosine function is a function whose domain is the set of all real numbers and range is the set [-1, 1]. If we restrict the domain of cosine function to \([0, \pi]\), then it becomes one-one and onto with range [-1, 1]. Actually, cosine function restricted to any of the intervals \([-\pi, 0]\), \([0, \pi]\), \([\pi, 2\pi]\) etc., is bijective with range as [-1, 1]. We can, therefore, define the inverse of cosine function in each of these intervals. We denote the inverse of the cosine function by \(cos^{-1}\) (arc cosine function). Thus, \(cos^{-1}\) is a function whose domain is [-1, 1] and range could be any of the intervals \([-\pi, 0]\), \([0, \pi]\), \([\pi, 2\pi]\) etc. Corresponding to each such interval, we get a branch of the function \(cos^{-1}\). The branch with range \([0, \pi]\) is called the principal value branch of the function \(cos^{-1}\). We write \(cos^{-1}: [-1, 1] \rightarrow [0, \pi]\).
Cos Graph
The graph of the function given by \(y =
cos^{-1}x\) can be drawn in the same way as discussed about the
graph of \(y=sin^{-1}x\). The graphs of
\(y=cos~x\) and \(y=cos^{-1}x\) are given in Fig 2.2 (i) and
(ii). 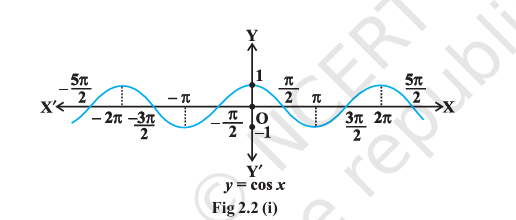
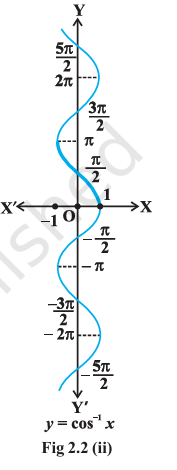
Cos Function and Its Domain Restrictions
Let us now discuss \(cosec^{-1}x\) and \(sec^{-1}x\) as follows: Since, \(cosec~x = \frac{1}{sin~x}\), the domain of the cosec function is the set \(\{x : x \in R \text{ and } x \neq n\pi, n \in Z\}\) and the range is the set \(\{y : y \in R, y \ge 1 \text{ or } y \le -1\}\) i.e., the set \(R - (-1, 1)\). It means that \(y = cosec~x\) assumes all real values except \(-1 < y < 1\) and is not defined for integral multiple of \(\pi\). If we restrict the domain of cosec function to \([-\frac{\pi}{2}, \frac{\pi}{2}] - \{0\}\), then it is one to one and onto with its range as the set \(R - (-1, 1)\). Actually, cosec function restricted to any of the intervals \([\frac{-3\pi}{2}, \frac{-\pi}{2}] - \{-\pi\}, [\frac{-\pi}{2}, \frac{\pi}{2}] - \{0\}, [\frac{\pi}{2}, \frac{3\pi}{2}] - \{\pi\}\) etc., is bijective and its range is the set of all real numbers \(R - (-1, 1)\). Thus \(cosec^{-1}\) can be defined as a function whose domain is \(R - (-1, 1)\) and range could be any of the intervals \([\frac{-3\pi}{2}, \frac{-\pi}{2}] - \{-\pi\}\), \([\frac{-\pi}{2}, \frac{\pi}{2}] - \{0\}\), \([\frac{\pi}{2}, \frac{3\pi}{2}] - \{\pi\}\) etc. The function corresponding to the range \([\frac{-\pi}{2}, \frac{\pi}{2}] - \{0\}\) is called the principal value branch of \(cosec^{-1}\). We thus have principal branch as \(cosec^{-1}: R - (-1, 1) \rightarrow [-\frac{\pi}{2}, \frac{\pi}{2}] - \{0\}\).
Cosec Graph
The graphs of \(y = cosec~x\) and
\(y = cosec^{-1}x\) are given in Fig
2.3 (i), (ii). 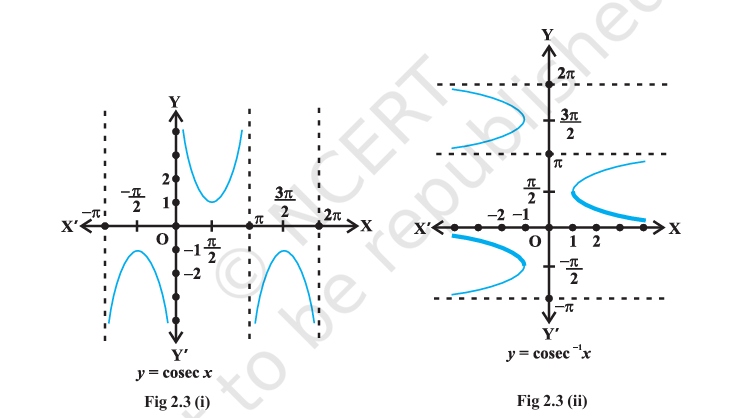
Sec Function and Its Domain Restrictions
Also, since \(sec~x = \frac{1}{cos~x}\), the domain of \(y=sec~x\) is the set \(R - \{x : x = (2n+1)\frac{\pi}{2}, n \in Z\}\) and range is the set \(R - (-1, 1)\). It means that sec (secant function) assumes all real values except \(-1 < y < 1\) and is not defined for odd multiples of \(\frac{\pi}{2}\). If we restrict the domain of secant function to \([0, \pi] - \{\frac{\pi}{2}\}\), then it is one-one and onto with its range as the set \(R - (-1, 1)\). Actually, secant function restricted to any of the intervals \([-\pi, 0] - \{-\frac{\pi}{2}\}\), \([0, \pi] - \{\frac{\pi}{2}\}\), \([\pi, 2\pi] - \{\frac{3\pi}{2}\}\) etc., is bijective and its range is \(R - \{-1, 1\}\). Thus \(sec^{-1}\) can be defined as a function whose domain is \(R - (-1, 1)\) and range could be any of the intervals \([-\pi, 0] - \{-\frac{\pi}{2}\}\), \([0, \pi] - \{\frac{\pi}{2}\}\), \([\pi, 2\pi] - \{\frac{3\pi}{2}\}\) etc. Corresponding to each of these intervals, we get different branches of the function \(sec^{-1}\). The branch with range \([0, \pi] - \{\frac{\pi}{2}\}\) is called the principal value branch of the function \(sec^{-1}\). We thus have \(sec^{-1}: R - (-1, 1) \rightarrow [0, \pi] - \{\frac{\pi}{2}\}\).
Sec Graph
The graphs of the functions \(y =
sec~x\) and \(y = sec^{-1}x\)
are given in Fig 2.4 (i), (ii). 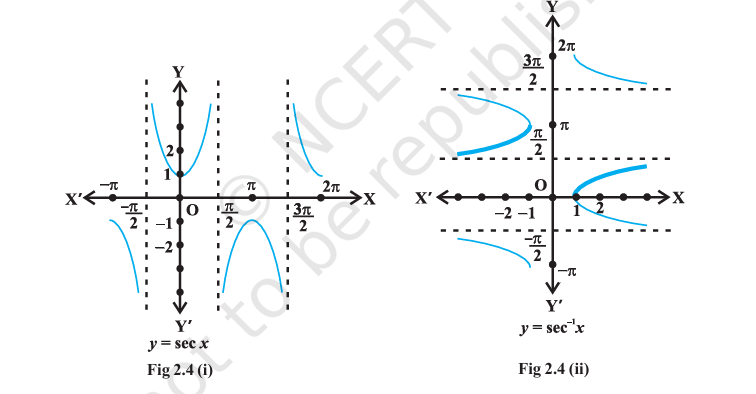
tan Function and Its Domain Restrictions
Finally, we now discuss \(tan^{-1}\) and \(cot^{-1}\). We know that the domain of the tan function (tangent function) is the set \(\{x: x \in R \text{ and } x \neq (2n+1)\frac{\pi}{2}, n \in Z\}\) and the range is R. It means that tan function is not defined for odd multiples of \(\frac{\pi}{2}\). If we restrict the domain of tangent function to \((\frac{-\pi}{2}, \frac{\pi}{2})\), then it is one-one and onto with its range as R. Actually, tangent function restricted to any of the intervals \((\frac{-3\pi}{2}, \frac{-\pi}{2}), (\frac{-\pi}{2}, \frac{\pi}{2}), (\frac{\pi}{2}, \frac{3\pi}{2})\) etc., is bijective and its range is R. Thus \(tan^{-1}\) can be defined as a function whose domain is R and range could be any of the intervals \((\frac{-3\pi}{2}, \frac{-\pi}{2}), (\frac{-\pi}{2}, \frac{\pi}{2}), (\frac{\pi}{2}, \frac{3\pi}{2})\) and so on. These intervals give different branches of the function \(tan^{-1}\). The branch with range \((\frac{-\pi}{2}, \frac{\pi}{2})\) is called the principal value branch of the function \(tan^{-1}\). We thus have \(tan^{-1}: R \rightarrow (\frac{-\pi}{2}, \frac{\pi}{2})\)
tan Graph
The graphs of the function \(y =
tan~x\) and \(y = tan^{-1}x\)
are given in Fig 2.5 (i), (ii). 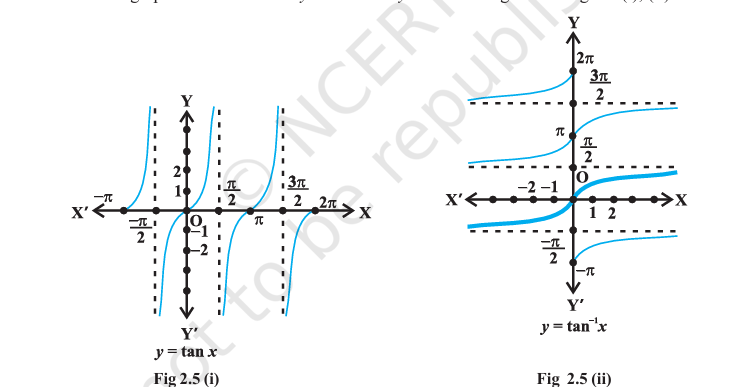
Cot Function and Its Domain Restrictions
We know that domain of the cot function (cotangent function) is the set \(\{x : x \in R \text{ and } x \neq n\pi, n \in Z\}\) and range is R. It means that cotangent function is not defined for integral multiples of \(\pi\). If we restrict the domain of cotangent function to \((0, \pi)\), then it is bijective with its range as R. In fact, cotangent function restricted to any of the intervals \((-\pi, 0), (0, \pi), (\pi, 2\pi)\) etc., is bijective and its range is R. Thus \(cot^{-1}\) can be defined as a function whose domain is the R and range as any of the intervals \((-\pi, 0), (0, \pi), (\pi, 2\pi)\) etc. These intervals give different branches of the function \(cot^{-1}\). The function with range \((0, \pi)\) is called the principal value branch of the function \(cot^{-1}\). We thus have \(cot^{-1}: R \rightarrow (0, \pi)\)
Cot Graph
The graphs of \(y = cot~x\) and
\(y = cot^{-1}x\) are given in Fig 2.6
(i), (ii). 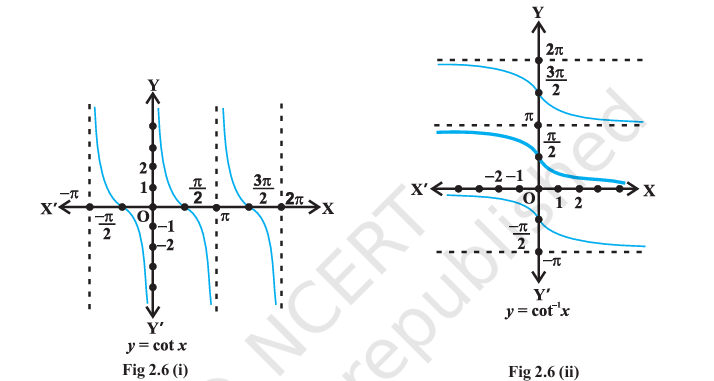
domains and ranges
The following table gives the inverse trigonometric function (principal value branches) along with their domains and ranges.
| Function | Domain | Range (Principal Value Branch) |
|---|---|---|
| \(sin^{-1}\) | \([-1, 1]\) | \([-\frac{\pi}{2}, \frac{\pi}{2}]\) |
| \(cos^{-1}\) | \([-1, 1]\) | \([0, \pi]\) |
| \(cosec^{-1}\) | \(R - (-1, 1)\) | \([-\frac{\pi}{2}, \frac{\pi}{2}] - \{0\}\) |
| \(sec^{-1}\) | \(R - (-1, 1)\) | \([0, \pi] - \{\frac{\pi}{2}\}\) |
| \(tan^{-1}\) | R | \((-\frac{\pi}{2}, \frac{\pi}{2})\) |
| \(cot^{-1}\) | R | \((0, \pi)\) |
Note
- \(sin^{-1}x\) should not be confused with \((sin x)^{-1}\). In fact \((sin x)^{-1} = \frac{1}{sin x}\) and similarly for other trigonometric functions.
- Whenever no branch of an inverse trigonometric functions is mentioned, we mean the principal value branch of that function.
- The value of an inverse trigonometric functions which lies in the range of principal branch is called the principal value of that inverse trigonometric functions.
Example 1
Find the principal value of \(sin^{-1}(\frac{1}{\sqrt{2}})\)Example 2
Find the principal value of \(cot^{-1}(\frac{-1}{\sqrt{3}})\)2.3 Properties of Inverse Trigonometric Functions
In this section, we shall prove some important properties of inverse trigonometric functions. It may be mentioned here that these results are valid within the principal value branches of the corresponding inverse trigonometric functions and wherever they are defined. Some results may not be valid for all values of the domains of inverse trigonometric functions. In fact, they will be valid only for some values of x for which inverse trigonometric functions are defined. We will not go into the details of these values of x in the domain as this discussion goes beyond the scope of this textbook.
Let us recall that if \(y = sin^{-1}x\), then \(x = sin y\) and if \(x = sin y\), then \(y = sin^{-1}x\). This is equivalent to \(sin(sin^{-1}x) = x, x \in [-1, 1]\) and \(sin^{-1}(sin x) = x, x \in [-\frac{\pi}{2}, \frac{\pi}{2}]\) For suitable values of domain similar results follow for remaining trigonometric functions.
Example 3
Show that (i) \(sin^{-1}(2x\sqrt{1-x^2}) = 2sin^{-1}x, -\frac{1}{\sqrt{2}} \le x \le \frac{1}{\sqrt{2}}\) (ii) \(sin^{-1}(2x\sqrt{1-x^2}) = 2cos^{-1}x, \frac{1}{\sqrt{2}} \le x \le 1\)Example 4
Express \(tan^{-1}(\frac{cos x}{1-sin x})\), \(-\frac{3\pi}{2} < x < \frac{\pi}{2}\) in the simplest form.Example 5
Write \(cot^{-1}(\frac{1}{\sqrt{x^2-1}})\), \(x > 1\) in the simplest form.Miscellaneous Examples
Example 6 Find the value of \(sin^{-1}(sin\frac{3\pi}{5})\)Summary
The domains and ranges (principal value branches) of inverse trigonometric functions are given in the following table:
| Functions | Domain | Range (Principal Value Branches) |
|---|---|---|
| y = \(sin^{-1}x\) | [-1, 1] | \([-\frac{\pi}{2}, \frac{\pi}{2}]\) |
| y = \(cos^{-1}x\) | [-1, 1] | \([0, \pi]\) |
| y = \(cosec^{-1}x\) | R – (–1, 1) | \([-\frac{\pi}{2}, \frac{\pi}{2}]\) – {0} |
| y = \(sec^{-1}x\) | R – (–1, 1) | \([0, \pi]\) – {<span class="math inline">\(\frac{\pi}{2}\)} |
| y = \(tan^{-1}x\) | R | \((-\frac{\pi}{2}, \frac{\pi}{2})\) |
| y = \(cot^{-1}x\) | R | \((0, \pi)\) |
\(sin^{-1}x\) should not be confused with \((sin x)^{-1}\). In fact \((sin x)^{-1} = \frac{1}{sin x}\) and similarly for other trigonometric functions.
The value of an inverse trigonometric functions which lies in its principal value branch is called the principal value of that inverse trigonometric functions.
For suitable values of domain, we have \(y = sin^{-1}x \Rightarrow x = sin y\) \(x = sin y \Rightarrow y = sin^{-1}x\) \(sin(sin^{-1}x) = x\) \(sin^{-1}(sin x) = x\)
Historical Note
The study of trigonometry was first started in India. The ancient Indian Mathematicians, Aryabhata (476 A.D.), Brahmagupta (598 A.D.), Bhaskara I (600 A.D.) and Bhaskara II (1114 A.D.) got important results of trigonometry. All this knowledge went from India to Arabia and then from there to Europe. The Greeks had also started the study of trigonometry but their approach was so clumsy that when the Indian approach became known, it was immediately adopted throughout the world.
In India, the predecessor of the modern trigonometric functions, known as the sine of an angle, and the introduction of the sine function represents one of the main contribution of the siddhantas (Sanskrit astronomical works) to mathematics.
Bhaskara I (about 600 A.D.) gave formulae to find the values of sine functions for angles more than 90°. A sixteenth century Malayalam work Yuktibhasa contains a proof for the expansion of sin (A + B). Exact expression for sines or cosines of 18°, 36°, 54°, 72°, etc., were given by Bhaskara II.
The symbols \(sin^{-1}x\), \(cos^{-1}x\), etc., for arc sin x, arc cos x, etc., were suggested by the astronomer Sir John F.W. Hersehel (1813). The name of Thales (about 600 B.C.) is invariably associated with height and distance problems. He is credited with the determination of the height of a great pyramid in Egypt by measuring shadows of the pyramid and an auxiliary staff (or gnomon) of known height, and comparing the ratios: \(\frac{H}{S} = \frac{h}{s} = tan(\text{sun's altitude})\) Thales is also said to have calculated the distance of a ship at sea through the proportionality of sides of similar triangles. Problems on height and distance using the similarity property are also found in ancient Indian works.
—v—
Exercise 1
Find the value of: \(\sin^{-1}(-\frac{1}{2})\)
Exercise 2
Find the value of: \(\cos^{-1}(\frac{\sqrt{3}}{2})\)
Exercise 3
Find the value of: \(\csc^{-1}(2)\)
Exercise 4
Find the value of: \(\tan^{-1}(-\sqrt{3})\)
Exercise 5
Find the value of: \(\cos^{-1}(-\frac{1}{2})\)
Exercise 6
Find the value of: \(\tan^{-1}(-1)\)
Exercise 7
Find the value of: \(\sec^{-1}(\frac{2}{\sqrt{3}})\)
Exercise 8
Find the value of: \(\cot^{-1}(\sqrt{3})\)
Exercise 9
Find the value of: \(\cos^{-1}(-\frac{1}{\sqrt{2}})\)
Exercise 10
Find the value of: \(\csc^{-1}(-\sqrt{2})\)
Exercise 11
Find the value of: \(\tan^{-1}(1) + \cos^{-1}(-\frac{1}{2}) + \sin^{-1}(-\frac{1}{2})\)
Exercise 12
Find the value of: \(\cos^{-1}(\frac{1}{2}) + 2 \sin^{-1}(\frac{1}{2})\)
Exercise 13
If \(\sin^{-1}x = y\), then: (A) \(0 \le y \le \pi\) (B) \(-\frac{\pi}{2} \le y \le \frac{\pi}{2}\) (C) \(0 < y < \pi\) (D) \(-\frac{\pi}{2} < y < \frac{\pi}{2}\)
Exercise 14
\(\tan^{-1}\sqrt{3} - \sec^{-1}(-2)\) is equal to: (A) \(\pi\) (B) \(-\frac{\pi}{3}\) (C) \(\frac{\pi}{3}\) (D) \(\frac{2\pi}{3}\)
Exercise 15
Prove the following: \(3\sin^{-1}x = \sin^{-1}(3x - 4x^3), x \in [-\frac{1}{2}, \frac{1}{2}]\)
Exercise 16
Prove the following: \(3\cos^{-1}x = \cos^{-1}(4x^3 - 3x), x \in [\frac{1}{2}, 1]\)
Exercise 17
Write the following function in the simplest form: \(\tan^{-1}\frac{\sqrt{1+x^2}-1}{x}, x \neq 0\)
Exercise 18
Write the following function in the simplest form: \(\tan^{-1}(\sqrt{\frac{1-\cos x}{1+\cos x}}), 0 < x < \pi\)
Exercise 19
Write the following function in the simplest form: \(\tan^{-1}(\frac{\cos x - \sin x}{\cos x + \sin x}), -\frac{\pi}{4} < x < \frac{3\pi}{4}\)
Exercise 20
Write the following function in the simplest form: \(\tan^{-1}\frac{x}{\sqrt{a^2-x^2}}, |x| < a\)
Exercise 21
Write the following function in the simplest form: \(\tan^{-1}(\frac{3a^2x - x^3}{a^3 - 3ax^2}), a > 0; -\frac{a}{\sqrt{3}} < x < \frac{a}{\sqrt{3}}\)
Exercise 22
Find the value of: \(\tan^{-1}[2\cos(2\sin^{-1}\frac{1}{2})]\)
Exercise 23
Find the value of: \(\tan\frac{1}{2}[\sin^{-1}\frac{2x}{1+x^2} + \cos^{-1}\frac{1-y^2}{1+y^2}], |x| < 1, y > 0 \text{ and } xy < 1\)
Exercise 24
Find the value of the expression: \(\sin^{-1}(\sin\frac{2\pi}{3})\)
Exercise 25
Find the value of the expression: \(\tan^{-1}(\tan\frac{3\pi}{4})\)
Exercise 26
Find the value of the expression: \(\tan(\sin^{-1}\frac{3}{5} + \cot^{-1}\frac{3}{2})\)
Exercise 27
\(\cos^{-1}(\cos\frac{7\pi}{6})\) is equal to: (A) \(\frac{7\pi}{6}\) (B) \(\frac{5\pi}{6}\) (C) \(\frac{\pi}{3}\) (D) \(\frac{\pi}{6}\)
Exercise 28
\(\sin(\frac{\pi}{3} - \sin^{-1}(-\frac{1}{2}))\) is equal to: (A) \(\frac{1}{2}\) (B) \(\frac{1}{3}\) (C) \(\frac{1}{4}\) (D) 1
Exercise 29
\(\tan^{-1}\sqrt{3} - \cot^{-1}(-\sqrt{3})\) is equal to: (A) \(\pi\) (B) \(-\frac{\pi}{2}\) (C) 0 (D) \(2\sqrt{3}\)
Exercise 30
Find the value of: \(\cos^{-1}(\cos\frac{13\pi}{6})\)
Exercise 31
Find the value of: \(\tan^{-1}(\tan\frac{7\pi}{6})\)
Exercise 32
Prove that: \(2\sin^{-1}\frac{3}{5} = \tan^{-1}\frac{24}{7}\)
Exercise 33
Prove that: \(\sin^{-1}\frac{8}{17} + \sin^{-1}\frac{3}{5} = \tan^{-1}\frac{77}{36}\)
Exercise 34
Prove that: \(\cos^{-1}\frac{4}{5} + \cos^{-1}\frac{12}{13} = \cos^{-1}\frac{33}{65}\)
Exercise 35
Prove that: \(\cos^{-1}\frac{12}{13} + \sin^{-1}\frac{3}{5} = \sin^{-1}\frac{56}{65}\)
Exercise 36
Prove that: \(\tan^{-1}\frac{63}{16} = \sin^{-1}\frac{5}{13} + \cos^{-1}\frac{3}{5}\)
Exercise 37
Prove that: \(\tan^{-1}\frac{1}{x} = \cos^{-1}(\frac{x}{\sqrt{1+x^2}}), x \in [0, 1]\)
Exercise 38
Prove that: \(\cot^{-1}(\frac{\sqrt{1+\sin x} + \sqrt{1-\sin x}}{\sqrt{1+\sin x} - \sqrt{1-\sin x}}) = \frac{x}{2}, x \in (0, \frac{\pi}{4})\)
Exercise 39
Prove that: \(\tan^{-1}(\frac{\sqrt{1+x} - \sqrt{1-x}}{\sqrt{1+x} + \sqrt{1-x}}) = \frac{\pi}{4} - \frac{1}{2}\cos^{-1}x, -\frac{1}{\sqrt{2}} \le x \le 1\)
Exercise 40
Solve the following equation: \(2\tan^{-1}(\cos x) = \tan^{-1}(2\csc x)\)
Exercise 41
Solve the following equation: \(\tan^{-1}\frac{1-x}{1+x} = \frac{1}{2}\tan^{-1}x, (x > 0)\)
Exercise 42
\(\sin(\tan^{-1}x), |x| < 1\) is equal to: (A) \(\frac{x}{\sqrt{1-x^2}}\) (B) \(\frac{1}{\sqrt{1-x^2}}\) (C) \(\frac{1}{\sqrt{1+x^2}}\) (D) \(\frac{x}{\sqrt{1+x^2}}\)
Exercise 43
If \(\sin^{-1}(1-x) - 2\sin^{-1}x = \frac{\pi}{2}\), then x is equal to: (A) 0, \(\frac{1}{2}\) (B) 1, \(\frac{1}{2}\) (C) 0 (D) \(\frac{1}{2}\)