Determinants
| Site: | Freebirds Moodle |
| Course: | NCERT XIIth Mathematics |
| Book: | Determinants |
| Printed by: | Guest user |
| Date: | Monday, 18 August 2025, 8:44 PM |
Table of contents
- Chapter 4
- 4.1 Introduction
- 4.2 Determinant
- Remarks
- Example 1
- Example 2 Evaluate $|\begin{smallmatrix}x&x+1\\ x-1&x\end{smallmatrix}|$
- 4.2.3 Determinant of a matrix of order 3x3
- Expansion along second row (R2)
- Expansion along first Column (C1)
- Remarks
- Example 3** Evaluate the determinant $\Delta=|\begin{smallmatrix}1&2&4\\ -1&3&0\\ 4&1&0\end{smallmatrix}|$
- Example 4
- Example 5
- 4.3 Area of a Triangle
- Example 6
- Example 7
- 4.4 Minors and Cofactors
- Example 8
- Definition 2
- Example 9
- Example 10
- Remark
- Example 11
- 4.5 Adjoint and Inverse of a Matrix
- Example 12
- Remark
- Theorem 1
- Remark
- Theorem 4
- Example 13
- Example 14
- Example 15
- 4.6 Applications of Determinants and Matrices
- cases
- Example 16
- Example 17
- Example 18
- Miscellaneous Examples 19
- Miscellaneous Example 20
- Miscellaneous Example 20
- Example 22
- Example 23
- Summary
- Historical Note
- EXERCISE 4.1.1
- EXERCISE 4.1.2
- EXERCISE 4.1.3
- EXERCISE 4.1.4
- EXERCISE 4.1.5
- EXERCISE 4.1.6
- EXERCISE 4.1.7
- EXERCISE 4.1.8
- Exercise 4.2.1
- Exercise 4.2.2
- Exercise 4.2.3
- Exercise 4.2.4
- Exercise 4.2.5
- Exercise 4.3.1
- Exercise 4.3.2
- Exercise 4.3.3
- Exercise 4.3.4
- Exercise 4.3.5
- Exercise 4.4.1
- Exercise 4.4.2
- Exercise 4.4.3
- Exercise 4.4.4
- Exercise 4.4.5
- Exercise 4.4.6
- Exercise 4.4.7
- Exercise 4.4.8
- Exercise 4.4.9
- Exercise 4.4.10
- Exercise 4.4.11
- Exercise 4.4.12
- Exercise 4.4.13
- Exercise 4.4.14
- Exercise 4.4.15
- Exercise 4.4.16
- Exercise 4.4.17
- Exercise 4.4.18
- Exercise 4.5.1
- Exercise 4.5.2
- Exercise 4.5.3
- Exercise 4.5.4
- Exercise 4.5.5
- Exercise 4.5.6
- Exercise 4.5.7
- Exercise 4.5.8
- Exercise 4.5.9
- Exercise 4.5.10
- Exercise 4.5.11
- Exercise 4.5.12
- Exercise 4.5.13
- Exercise 4.5.14
- Exercise 4.5.15
- Exercise 4.5.16
- Exercise 4.11
- Exercise 4.12
- Exercise 4.13
- Exercise 4.14
- Exercise 4.15
- Exercise 4.16
- Exercise 4.17
- Exercise 4.18
- Exercise 4.19
Chapter 4
DETERMINANTS
All Mathematical truths are relative and conditional. — C.P. STEINMETZ
P.S. Laplace (1749-1827)
4.1 Introduction
In the previous chapter, we have studied about matrices and algebra of matrices. We have also learnt that a system of algebraic equations can be expressed in the form of matrices. This means, a system of linear equations like \(a_{1}x+b_{1}y=c_{1}\) \(a_{2}x+b_{2}y=c_{2}\) can be represented as \([\begin{smallmatrix}a_{1}&b_{1}\\ a_{2}&b_{2}\end{smallmatrix}][\begin{smallmatrix}x\\ y\end{smallmatrix}]=[\begin{smallmatrix}c_{1}\\ c_{2}\end{smallmatrix}]\). Now, this system of equations has a unique solution or not, is determined by the number \(a_{1}b_{2}-a_{2}b_{1}.\) (Recall that if \(\frac{a_{1}}{a_{2}}\ne\frac{b_{1}}{b_{2}}\) or, \(a_{1}b_{2}-a_{2}b_{1}\ne0\) then the system of linear equations has a unique solution). The number \(a_{1}b_{2}-a_{2}b_{1}\) which determines uniqueness of solution is associated with the matrix \(A=[\begin{smallmatrix}a_{1}&b_{1}\\ a_{2}&b_{2}\end{smallmatrix}]\) and is called the determinant of A or det A. Determinants have wide applications in Engineering, Science, Economics, Social Science, etc.
In this chapter, we shall study determinants up to order three only with real entries. Also, we will study various properties of determinants, minors, cofactors and applications of determinants in finding the area of a triangle, adjoint and inverse of a square matrix, consistency and inconsistency of system of linear equations and solution of linear equations in two or three variables using inverse of a matrix.
4.2 Determinant
To every square matrix \(A=[a_{ij}]\) of order n, we can associate a number (real or complex) called determinant of the square matrix A, where \(a_{ij}=(i,j)^{ih}\) element of A. Reprint 2025-26 This may be thought of as a function which associates each square matrix with a unique number (real or complex). If M is the set of square matrices, K is the set of numbers (real or complex) and \(f:M\rightarrow K\) is defined by \(f(A)=k\) where \(A\in M\) and \(k\in K\), then \(f(A)\) is called the determinant of A. It is also denoted by | \(|A|\) or det A or A.
If \(A=[\begin{smallmatrix}a&b\\ c&d\end{smallmatrix}],\) then determinant of A is written as \(|A|=|\begin{smallmatrix}a&b\\ c&d\end{smallmatrix}|=det(A)\)
Remarks
- For matrix A, \(|A|\) is read as determinant of A and not modulus of A.
- Only square matrices have determinants.
4.2.1 Determinant of a matrix of order one
Let \(A=[a]\) be the matrix of order 1, then determinant of A is defined to be equal to a
4.2.2 Determinant of a matrix of order two
Let \(A=[\begin{smallmatrix}a_{11}&a_{12}\\ a_{21}&a_{22}\end{smallmatrix}]\) be a matrix of order \(2\times2\) of order 2 then the determinant of A is defined as: \(det(A)=|A|=\Delta=|\begin{smallmatrix}a_{11}&a_{12}\\ a_{21}&a_{22}\end{smallmatrix}|=a_{11}a_{22}-a_{21}a_{12}\)
Example 1
Evaluate \(|\begin{smallmatrix}2&4\\ -1&2\end{smallmatrix}|\)Example 2 Evaluate $|\begin{smallmatrix}x&x+1\\ x-1&x\end{smallmatrix}|$
4.2.3 Determinant of a matrix of order 3x3
Determinant of a matrix of order three can be determined by expressing it in terms of second order determinants. This is known as expansion of a determinant along a row (or a column). There are six ways of expanding a determinant of order 3 corresponding to each of three rows \((R_{1}\), \(R_{2}\) and \(R_{3}\)) and three columns \((C_{1}\), \(C_{2}\) and \(C_{3})\) giving the same value as shown below.
Consider the determinant of square matrix \(A=[a_{ij}]_{3\times3}\) i.e., \(|A|=|\begin{smallmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{smallmatrix}|\)
Expansion along first Row (R1)
Step 1 Multiply first element \(a_{11}\) of \(R_{1}\) by \((-1)^{(1+1)}[(-1)^{\text{sum of suffixes in } a_{11}}]\) and with the second order determinant obtained by deleting the first row and first column \((C_{1})\) of \(|A|\) as \(a_{11}\) lies in \(R_{1}\) and \(C_{1}\), i.e., \((-1)^{1+1}a_{11}|\begin{smallmatrix}a_{22}&a_{23}\\ a_{32}&a_{33}\end{smallmatrix}|\)
Step 2 Multiply 2nd element \(a_{12}\) of \(R_{1}\) by \((-1)^{1+2}[(-1)^{\text{sum of suffixes in } a_{12}}]\) and the second order determinant obtained by deleting the first row \((R_{1})\) and second column \((C_{2})\) of \(|A|\) as \(a_{12}\) lies in \(R_{1}\) and \(C_{2},\) i.e., \((-1)^{1+2}a_{12}|\begin{smallmatrix}a_{21}&a_{23}\\ a_{31}&a_{33}\end{smallmatrix}|\)
Step 3 Multiply 3rd element of \(R_{1}\) by \((-1)^{1+3}[(-1)^{\text{sum of suffixes in } a_{13}}]\) and the second order determinant obtained by deleting the first row \((R_{1})\) and third column \((C_{3})\) of \(|A|\) as \(a_{13}\) lies in \(R_{1}\) and \(C_{3}\). i.e., \((-1)^{1+3}a_{13}|\begin{smallmatrix}a_{21}&a_{22}\\ a_{31}&a_{32}\end{smallmatrix}|\)
Step 4 Finally, the expansion of the determinant of A, that is, \(|A|\) written as the sum of all three terms obtained in steps 1, 2 and 3 above is given by \(|A|=(-1)^{1+1}a_{11}|\begin{smallmatrix}a_{22}&a_{23}\\ a_{32}&a_{33}\end{smallmatrix}|+(-1)^{1+2}a_{12}|\begin{smallmatrix}a_{21}&a_{23}\\ a_{31}&a_{33}\end{smallmatrix}| +(-1)^{1+3}a_{13}|\begin{smallmatrix}a_{21}&a_{22}\\ a_{31}&a_{32}\end{smallmatrix}|\) or \(|A|=a_{11}(a_{22}a_{33}-a_{32}a_{23})-a_{12}(a_{21}a_{33}-a_{31}a_{23}) +a_{13}(a_{21}a_{32}-a_{31}a_{22})\) \(=a_{11}a_{22}a_{33}-a_{11}a_{32}a_{23}-a_{12}a_{21}a_{33}+a_{12}a_{31}a_{23}+a_{13}a_{21}a_{32}\) \(-a_{13} a_{31} a_{22}\)
Expansion along second row (R2)
Expanding along \(R_{2}\) we get \(|A|=|\begin{smallmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{smallmatrix}|\) \(|A|=(-1)^{2+1}a_{21}|\begin{smallmatrix}a_{12}&a_{13}\\ a_{32}&a_{33}\end{smallmatrix}|+(-1)^{2+2}a_{22}|\begin{smallmatrix}a_{11}&a_{13}\\ a_{31}&a_{33}\end{smallmatrix}| +(-1)^{2+3}a_{23}|\begin{smallmatrix}a_{11}&a_{12}\\ a_{31}&a_{32}\end{smallmatrix}|\) \(=-a_{21}(a_{12}a_{33}-a_{32}a_{13})+a_{22}(a_{11}a_{33}-a_{31}a_{13})\) \(-a_{23}(a_{11}a_{32}-a_{31}a_{12})\) \(|A|=-a_{21}a_{12}a_{33}+a_{21}a_{32}a_{13}+a_{22}a_{11}a_{33}-a_{22}a_{31}a_{13}-a_{23}a_{11}a_{32}\) + A23 A31 A12 \(=a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\) \(-a_{13}a_{31}a_{22}\)
Expansion along first Column (C1)
By expanding along \(C_{1}\) we get \(|A|=|\begin{smallmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{smallmatrix}|\) \(|A|=a_{11}(-1)^{1+1}|\begin{smallmatrix}a_{22}&a_{23}\\ a_{32}&a_{33}\end{smallmatrix}|+a_{21}(-1)^{2+1}|\begin{smallmatrix}a_{12}&a_{13}\\ a_{32}&a_{33}\end{smallmatrix}| +a_{31}(-1)^{3+1}|\begin{smallmatrix}a_{12}&a_{13}\\ a_{22}&a_{23}\end{smallmatrix}|\) \(=a_{11}(a_{22}a_{33}-a_{23}a_{32})-a_{21}(a_{12}a_{33}-a_{13}a_{32})+a_{31}(a_{12}a_{23}-a_{13}a_{22})\) \(|A|=a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}-a_{21}a_{12}a_{33}+a_{21}a_{13}a_{32}+a_{31}a_{12}a_{23}\) \(-a_{13}a_{31}a_{22}\) \(-a_{31}a_{13}a_{22}\) \(=a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\) (3)
Clearly, values of A in (1), (2) and (3) are equal. It is left as an exercise to the reader to verify that the values of |A| by expanding along \(R_{3}\), \(C_{2}\) and \(C_{3}\) are equal to the value of \(|A|\) obtained in (1), (2) or (3).
Hence, expanding a determinant along any row or column gives same value.
Remarks
- For easier calculations, we shall expand the determinant along that row or column which contains maximum number of zeros.
- While expanding, instead of multiplying by \((-1)^{i+j}\), we can multiply by +1 or-1 according as \((i+j)\) is even or odd.
- Let \(A=[\begin{smallmatrix}2&2\\ 4&0\end{smallmatrix}]\) and \(B=[\begin{smallmatrix}1&1\\ 2&0\end{smallmatrix}]\) Then, it is easy to verify that \(A=2B\) Also \(|A|=0-8=-8\) and \(|B|=0-2=-2.\) Observe that, \(|A|=4(-2)=2^{2}|B|\) or \(|A|=2^{n}|B|\) , where \(n=2\) is the order of square matrices A and B.
In general, if \(A=kB\) where A and B are square matrices of order n, then | \(A|=k^{n}\) | B , where \(n=1,2,3\)
Example 3** Evaluate the determinant $\Delta=|\begin{smallmatrix}1&2&4\\ -1&3&0\\ 4&1&0\end{smallmatrix}|$
Example 4
Evaluate \(\Delta=|\begin{smallmatrix}0&sin~\alpha&-cos~\alpha\\ -sin~\alpha&0&sin~\beta\\ cos~\alpha&-sin~\beta&0\end{smallmatrix}|.\)Example 5
Find values of x for which \(|\begin{smallmatrix}3&x\\ x&1\end{smallmatrix}|=|\begin{smallmatrix}3&2\\ 4&1\end{smallmatrix}|\)4.3 Area of a Triangle
In earlier classes, we have studied that the area of a triangle whose vertices are \((x_{1},y_{1})\), \((x_2, y_2)\) and \((x_{3},y_{3})\), is given by the expression \(\frac{1}{2}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+ x_{3}(y_{1}-y_{2})]\) Now this expression can be written in the form of a determinant as \(A=\frac{1}{2}|\begin{smallmatrix}x_{1}&y_{1}&1\\ x_{2}&y_{2}&1\\ x_{3}&y_{3}&1\end{smallmatrix}|\)
Remarks
- Since area is a positive quantity, we always take the absolute value of the determinant in (1).
- If area is given, use both positive and negative values of the determinant for calculation.
- The area of the triangle formed by three collinear points is zero.
Example 6
Find the area of the triangle whose vertices are (3, 8), (-4, 2) and (5, 1).Example 7
Find the equation of the line joining \(A(1,3)\) and B (0, 0) using determinants and find k if \(D(k,0)\) is a point such that area of triangle ABD is 3sq units.4.4 Minors and Cofactors
In this section, we will learn to write the expansion of a determinant in compact form using minors and cofactors.
Definition 1 Minor of an element \(a_{ij}\) of a determinant is the determinant obtained by deleting its ith row and jth column in which element \(a_{ij}\) lies. Minor of an element \(a_{ij}\) is denoted by \(M_{ij}\)
Remark Minor of an element of a determinant of order \(n(n\ge2)\) is a determinant of order \(n-1\).
Example 8
Find the minor of element 6 in the determinant \(\Delta=|\begin{smallmatrix}1&2&3\\ 4&5&6\\ 7&8&9\end{smallmatrix}|\)Definition 2
Cofactor of an element \(a_{ij}\), denoted by \(A_{ij}\) is defined by \(A_{ij}=(-1)^{i+j}M_{ij}\) where \(M_{ij}\) is minor of \(a_{ij}.\)
Example 9
Find minors and cofactors of all the elements of the determinant \(|\begin{smallmatrix}1&-2\\ 4&3\end{smallmatrix}|\)Example 10
Find the minors and cofactors of the elements \(a_{11}, a_{21}\) in the determinant \(\Delta = |\begin{smallmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{smallmatrix}|\)Remark
If elements of a row (or column) are multiplied with cofactors of any other row (or column), then their sum is zero. For example, \(\Delta = a_{11}A_{11} + a_{12}A_{12} + a_{13}A_{13}\) But \(a_{11}A_{21} + a_{12}A_{22} + a_{13}A_{23} = a_{11}(-1)^{2+1}|\begin{smallmatrix} a_{12} & a_{13} \\ a_{32} & a_{33} \end{smallmatrix}| + a_{12}(-1)^{2+2}|\begin{smallmatrix} a_{11} & a_{13} \\ a_{31} & a_{33} \end{smallmatrix}| + a_{13}(-1)^{2+3}|\begin{smallmatrix} a_{11} & a_{12} \\ a_{31} & a_{32} \end{smallmatrix}|\) \(= -a_{11}(a_{12}a_{33} - a_{13}a_{32}) + a_{12}(a_{11}a_{33} - a_{13}a_{31}) - a_{13}(a_{11}a_{32} - a_{12}a_{31})\) \(= -a_{11}a_{12}a_{33} + a_{11}a_{13}a_{32} + a_{12}a_{11}a_{33} - a_{12}a_{13}a_{31} - a_{13}a_{11}a_{32} + a_{13}a_{12}a_{31} = 0\) Similarly, we can try for other rows and columns.
Example 11
Find minors and cofactors of the elements of the determinant \(|\begin{smallmatrix} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{smallmatrix}|\) and verify that \(a_{11}A_{31} + a_{12}A_{32} + a_{13}A_{33} = 0\)4.5 Adjoint and Inverse of a Matrix
In the previous chapter, we have studied inverse of a matrix. In this section, we shall discuss the condition for existence of inverse of a matrix. To find inverse of a matrix, we shall first define adjoint of a matrix.
4.5.1 Adjoint of a matrix
Definition 3 The adjoint of a square matrix \(A = [a_{ij}]_{n \times n}\) is defined as the transpose of the matrix \([A_{ij}]_{n \times n}\), where \(A_{ij}\) is the cofactor of the element \(a_{ij}\). Adjoint of the matrix A is denoted by adj A. Let \(A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}\) Then \(adj A = Transpose of \begin{bmatrix} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \end{bmatrix} = \begin{bmatrix} A_{11} & A_{21} & A_{31} \\ A_{12} & A_{22} & A_{32} \\ A_{13} & A_{23} & A_{33} \end{bmatrix}\)
Example 12
Find adj A for \(A = \begin{bmatrix} 2 & 3 \\ 1 & 4 \end{bmatrix}\)Remark
For a square matrix of order 2, given by \(A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21}
& a_{22} \end{bmatrix}\). The adj A can also be obtained by
interchanging \(a_{11}\) and \(a_{22}\) and by changing signs of \(a_{12}\) and \(a_{21}\), i.e., 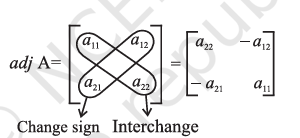 We state the following theorem without proof.
We state the following theorem without proof.
Theorem 1
If A be any given square matrix, then \(A(adj A) = (adj A)A = |A|I\), where I is the identity matrix of the same order A.
Verification Let \(A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}\), then \(adj A = \begin{bmatrix} A_{11} & A_{21} & A_{31} \\ A_{12} & A_{22} & A_{32} \\ A_{13} & A_{23} & A_{33} \end{bmatrix}\) Since sum of product of elements of a row with their corresponding cofactors is equal to \(|A|\) and otherwise zero, we have \(A(adj A) = \begin{bmatrix} |A| & 0 & 0 \\ 0 & |A| & 0 \\ 0 & 0 & |A| \end{bmatrix} = |A|\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = |A|I\) Similarly, we can verify \((adj A) A = |A| I\) Hence A (adj A) = (adj A) A = |A| I
Definition 4 A square matrix A is said to be singular if \(|A| = 0\). Definition 5 A square matrix A is said to be non-singular if \(|A| \neq 0\).
We state the following theorems without proof. Theorem 2 If A and B are nonsingular matrices of the same order, then AB and BA are also nonsingular matrices of the same order. Theorem 3 The determinant of the product of matrices is equal to product of their respective determinants, that is, \(|AB| = |A| |B|\), where A and B are square matrices of the same order.
Remark
We know that \((adj A)A = |A|I = \begin{bmatrix} |A| & 0 & 0 \\ 0 & |A| & 0 \\ 0 & 0 & |A| \end{bmatrix}\) Taking determinant of both sides, we get \(|(adj A)A| = \begin{vmatrix} |A| & 0 & 0 \\ 0 & |A| & 0 \\ 0 & 0 & |A| \end{vmatrix}\) \(|adj A| |A| = |A|^3 \begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix} = |A|^3(1) = |A|^3\) In general, if A is a square matrix of order n, then \(|adj(A)| = |A|^{n-1}\).
Theorem 4
A square matrix A is invertible if and only if A is nonsingular matrix. Proof Let A be an invertible matrix of order n and I be the identity matrix of order n. Then there exists a square matrix B of order n such that \(AB = BA = I\). Now \(AB = I\). So \(|AB| = |I|\) or \(|A| |B| = 1\) This gives \(|A| \neq 0\). Hence A is nonsingular. Conversely, let A be nonsingular. Then \(|A| \neq 0\). Now \(A(adj A) = (adj A)A = |A| I\) (Theorem 1) or \(A(\frac{1}{|A|}adj A) = (\frac{1}{|A|}adj A)A = I\) or \(AB = BA = I\), where \(B = \frac{1}{|A|}adj A\) Thus A is invertible and \(A^{-1} = \frac{1}{|A|}adj A\)
Example 13
If \(A = \begin{bmatrix} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 1 & 3 & 4 \end{bmatrix}\), then verify that \(A(adj A) = |A|I\). Also find \(A^{-1}\).Example 14
If \(A = \begin{bmatrix} 2 & 3 \\ 1 & -4 \end{bmatrix}\) and \(B = \begin{bmatrix} 1 & -2 \\ -1 & 3 \end{bmatrix}\), then verify that \((AB)^{-1} = B^{-1}A^{-1}\).Example 15
Show that the matrix \(A = \begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}\) satisfies the equation \(A^2 - 4A + I = O\), where I is \(2 \times 2\) identity matrix and O is \(2 \times 2\) zero matrix. Using this equation, find \(A^{-1}\).4.6 Applications of Determinants and Matrices
In this section, we shall discuss application of determinants and matrices for solving the system of linear equations in two or three variables and for checking the consistency of the system of linear equations.
Consistent system: A system of equations is said to be consistent if its solution (one or more) exists. Inconsistent system: A system of equations is said to be inconsistent if its solution does not exist.
Solution of system of linear equations using inverse of a matrix
Let us express the system of linear equations as a matrix equation and solve it using inverse of the coefficient matrix. Consider the system of equations \(a_1x + b_1y + c_1z = d_1\) \(a_2x + b_2y + c_2z = d_2\) \(a_3x + b_3y + c_3z = d_3\) Let \(A = \begin{bmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{bmatrix}\), \(X = \begin{bmatrix} x \\ y \\ z \end{bmatrix}\) and \(B = \begin{bmatrix} d_1 \\ d_2 \\ d_3 \end{bmatrix}\). Then, the given system of equations can be written as, \(AX = B\).
cases
Case I: If A is a nonsingular matrix, then its inverse exists. Now \(AX = B\) \(A^{-1}(AX) = A^{-1}B\) (premultiplying by \(A^{-1}\)) \((A^{-1}A)X = A^{-1}B\) (by associative property) \(IX = A^{-1}B\) \(X = A^{-1}B\) This matrix equation provides unique solution for the given system of equations as inverse of a matrix is unique. This method of solving system of equations is known as Matrix Method.
Case II: If A is a singular matrix, then \(|A| = 0\). In this case, we calculate \((adj A)B\). If \((adj A)B \neq O\), (O being zero matrix), then solution does not exist and the system of equations is called inconsistent. If \((adj A)B = O\), then system may be either consistent or inconsistent according as the system have either infinitely many solutions or no solution.
Example 16
Solve the system of equations \(2x + 5y = 1\) \(3x + 2y = 7\)Example 17
Solve the following system of equations by matrix method. \(3x - 2y + 3z = 8\) \(2x + y - z = 1\) \(4x - 3y + 2z = 4\)Example 18
The sum of three numbers is 6. If we multiply third number by 3 and add second number to it, we get 11. By adding first and third numbers, we get double of the second number. Represent it algebraically and find the numbers using matrix method.Miscellaneous Examples 19
If a, b, c are positive and unequal, show that value of the determinant \(\Delta = |\begin{smallmatrix} a & b & c \\ b & c & a \\ c & a & b \end{smallmatrix}|\) is negative.Miscellaneous Example 20
If a, b, c are in A.P, find value of \(|\begin{smallmatrix} 2y+4 & 5y+7 & 8y+a \\ 3y+5 & 6y+8 & 9y+b \\ 4y+6 & 7y+9 & 10y+c \end{smallmatrix}|\)Miscellaneous Example 20
Show that \(\Delta = |\begin{smallmatrix} (y+z)^2 & xy & zx \\ xy & (x+z)^2 & yz \\ xz & yz & (x+y)^2 \end{smallmatrix}| = 2xyz(x+y+z)^3\)Example 22
Use product \(\begin{bmatrix} 1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4 \end{bmatrix}\begin{bmatrix} -2 & 0 & 1 \\ 9 & 2 & -3 \\ 6 & 1 & -2 \end{bmatrix}\) to solve the system of equations \(x - y + 2z = 1\) \(2y - 3z = 1\) \(3x - 2y + 4z = 2\)Example 23
Prove that \(\Delta = |\begin{smallmatrix} a+bx & c+dx & p+qx \\ ax+b & cx+d & px+q \\ u & v & w \end{smallmatrix}| = (1-x^2)|\begin{smallmatrix} a & c & p \\ b & d & q \\ u & v & w \end{smallmatrix}|\)Summary
- Determinant of a matrix A = [a₁₁] of order 1 is given by |A| = a₁₁.
- Determinant of a matrix A = \(\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}\) of order 2 is given by \(|A| = a_{11}a_{22} - a_{12}a_{21}\).
- Determinant of a matrix A = \(\begin{bmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{bmatrix}\) of order 3 is given by \(|A| = a_1(b_2c_3 - b_3c_2) - b_1(a_2c_3 - a_3c_2) + c_1(a_2b_3 - a_3b_2)\).
- For any square matrix A, the area of a triangle with vertices \((x_1, y_1), (x_2, y_2)\) and \((x_3, y_3)\) is given by \(\frac{1}{2}|\begin{smallmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{smallmatrix}|\).
- Minor of an element \(a_{ij}\) of the determinant of matrix A is the determinant obtained by deleting the \(i^{th}\) row and \(j^{th}\) column.
- Cofactor of an element \(a_{ij}\) of the determinant of matrix A is \(A_{ij} = (-1)^{i+j} M_{ij}\).
- Value of determinant of a matrix A is obtained by the sum of the product of elements of a row (or a column) with their corresponding cofactors.
- If elements of a row (or column) are multiplied with cofactors of any other row (or column), then their sum is zero.
- Adjoint of A, denoted by adj A, is the transpose of the cofactor matrix.
- \(A(adj A) = (adj A)A = |A|I\).
- A square matrix A is said to be singular or non-singular according as \(|A|=0\) or \(|A| \neq 0\).
- If AB = BA = I, where B is the inverse of A, then \(A^{-1}=B\).
- \(A^{-1} = \frac{1}{|A|}(adj A)\).
- A system of linear equations is consistent if it has one or more solutions, and inconsistent if its solution does not exist.
- For a system of equations \(AX=B\):
- If \(|A| \neq 0\), there is a unique solution given by \(X=A^{-1}B\).
- If \(|A| = 0\) and \((adj A)B \neq 0\), then there is no solution.
- If \(|A| = 0\) and \((adj A)B = 0\), then the system has either no solution or infinitely many solutions.
Historical Note
The Chinese method of representing the coefficients of the unknowns of several linear equations by using rods on a calculating board led to the discovery of determinants. Two thousand years ago, the Chinese used this method to solve simultaneous equations, which is now known as Cramer’s rule.
The Japanese mathematician Seki Kowa is credited with the discovery of determinants in 1683. He used his method of solving simultaneous equations to find the roots of an equation. The German mathematician G.W. Leibniz also discovered determinants in 1693, and his work contains the expansion of a determinant.
In 1750, Cramer presented a rule for solving simultaneous equations, now known as Cramer’s Rule. However, this rule was likely known to Maclaurin as early as 1729.
The theory of determinants was further developed by Lagrange in 1773. He studied general determinants of the second and third order and applied them to questions of elimination.
In 1801, Gauss used determinants in his theory of numbers. The term ‘determinant’ was first introduced by him, though not in its present sense.
Cauchy was the first to use the term ‘determinant’ in its modern sense. He was the first to prove the general theorem on the multiplication of determinants and made significant contributions to the theory of determinants.
Jacobi also made important contributions to the theory of determinants. In 1841, he gave the general principles of determinants and introduced the functional determinant, which is now known as the Jacobian determinant.
EXERCISE 4.1.1
Evaluate the determinants in Exercises 1 and 2. \(|\begin{smallmatrix}2&4\\ -5&-1\end{smallmatrix}|\)
EXERCISE 4.1.2
Evaluate the determinants (i) \(|\begin{smallmatrix}cos~\theta&-sin~\theta\\ sin~\theta&cos~\theta\end{smallmatrix}|\) (ii) \(|\begin{smallmatrix}x^{2}-x+1&x-1\\ x+1&x+1\end{smallmatrix}|\) *
EXERCISE 4.1.3
Evaluate the determinants If \(A=[\begin{smallmatrix}1&2\\ 4&2\end{smallmatrix}]\) then show that \(|2A|=4|A|\)
EXERCISE 4.1.4
Evaluate the determinants If \(A=[\begin{smallmatrix}1&0&1\\ 0&1&2\\ 0&0&4\end{smallmatrix}],\) then show that \(|3~A|=27|A|\)
EXERCISE 4.1.5
Evaluate the determinants
\(|\begin{smallmatrix}3&-1&-2\\ 0&0&-1\\ 3&-5&0\end{smallmatrix}|\)
\(|\begin{smallmatrix}3&-4&5\\ 1&1&-2\\ 2&3&1\end{smallmatrix}|\)
\(|\begin{smallmatrix}0&1&2\\ -1&0&-3\\ -2&3&0\end{smallmatrix}|\)
\(|\begin{smallmatrix}2&-1&-2\\ 0&2&-1\\ 3&-5&0\end{smallmatrix}|\)
EXERCISE 4.1.6
If \(A=[\begin{smallmatrix}1&1&-2\\ 2&1&-3\\ 5&4&-9\end{smallmatrix}],\) find |A|
EXERCISE 4.1.7
Find values of x, if (i) \(|\begin{smallmatrix}2&4\\ 5&1\end{smallmatrix}|=|\begin{smallmatrix}2x&4\\ 6&x\end{smallmatrix}|\) (ii) \(|\begin{smallmatrix}2&3\\ 4&5\end{smallmatrix}|=|\begin{smallmatrix}x&3\\ 2x&5\end{smallmatrix}|\)
EXERCISE 4.1.8
If \(|\begin{smallmatrix}x&2\\
18&x\end{smallmatrix}|=|\begin{smallmatrix}6&2\\
18&6\end{smallmatrix}|\) then x is equal to (A) 6
(B) ± 6 (C) -6
Exercise 4.2.1
Find the area of the triangle with vertices at the point given in each of the following: (i) (1, 0), (6, 0), (4, 3) (ii) (2, 7), (1, 1), (10, 8) (iii) (-2, -3), (3, 2), (-1, -8)
Exercise 4.2.2
Show that points A(\(a, b+c\)), B(\(b, c+a\)), and C(\(c, a+b\)) are collinear.
Exercise 4.2.3
Find the values of \(k\) if the area of the triangle is 4 sq. units and the vertices are: (i) (\(k\), 0), (4, 0), (0, 2) (ii) (-2, 0), (0, 4), (0, \(k\))
Exercise 4.2.4
- Find the equation of the line joining (1, 2) and (3, 6) using determinants.
- Find the equation of the line joining (3, 1) and (9, 3) using determinants.
Exercise 4.2.5
If the area of a triangle is 35 sq units with vertices (2, -6), (5, 4), and (\(k\), 4), then \(k\) is: (A) 12 (B) -2 (C) -12, -2 (D) 12, -2
Exercise 4.3.1
Write the Minors and Cofactors of the elements of the following determinants: (i) \[\begin{vmatrix} 2 & -4 \\ 0 & 3 \end{vmatrix}\] (ii) \[\begin{vmatrix} a & c \\ b & d \end{vmatrix}\]
Exercise 4.3.2
Write the Minors and Cofactors of the elements of the following determinants: (i) \[\begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix}\] (ii) \[\begin{vmatrix} 1 & 0 & 4 \\ 3 & 5 & -1 \\ 0 & 1 & 2 \end{vmatrix}\]
Exercise 4.3.3
Using Cofactors of elements of the second row, evaluate: \[\Delta = \begin{vmatrix} 5 & 3 & 8 \\ 2 & 0 & 1 \\ 1 & 2 & 3 \end{vmatrix}\]
Exercise 4.3.4
Using Cofactors of elements of the third column, evaluate: \[\Delta = \begin{vmatrix} 1 & x & yz \\ 1 & y & zx \\ 1 & z & xy \end{vmatrix}\]
Exercise 4.3.5
If \(\Delta = \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}\) and \(A_{ij}\) is the Cofactor of \(a_{ij}\), then the value of \(\Delta\) is given by: (A) \(a_{11}A_{31} + a_{12}A_{32} + a_{13}A_{33}\) (B) \(a_{11}A_{11} + a_{12}A_{21} + a_{13}A_{31}\) (C) \(a_{21}A_{11} + a_{22}A_{12} + a_{23}A_{13}\) (D) \(a_{11}A_{11} + a_{21}A_{21} + a_{31}A_{31}\)
Exercise 4.4.1
Find the adjoint of the matrix: \[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\]
Exercise 4.4.2
Find the adjoint of the matrix: \[\begin{bmatrix} 1 & -1 & 2 \\ 2 & 3 & 5 \\ -2 & 0 & 1 \end{bmatrix}\]
Exercise 4.4.3
Verify \(A(\text{adj } A) = (\text{adj } A)A = |A|I\) for: \[A = \begin{bmatrix} 2 & 3 \\ -4 & -6 \end{bmatrix}\]
Exercise 4.4.4
Verify \(A(\text{adj } A) = (\text{adj } A)A = |A|I\) for: \[A = \begin{bmatrix} 1 & -1 & 2 \\ 3 & 0 & -2 \\ 1 & 0 & 3 \end{bmatrix}\]
Exercise 4.4.5
Find the inverse of the matrix (if it exists): \[\begin{bmatrix} 2 & -2 \\ 4 & 3 \end{bmatrix}\]
Exercise 4.4.6
Find the inverse of the matrix (if it exists): \[\begin{bmatrix} -1 & 5 \\ -3 & 2 \end{bmatrix}\]
Exercise 4.4.7
Find the inverse of the matrix (if it exists): \[\begin{bmatrix} 1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 5 \end{bmatrix}\]
Exercise 4.4.8
Find the inverse of the matrix (if it exists): \[\begin{bmatrix} 1 & 0 & 0 \\ 3 & 3 & 0 \\ 5 & 2 & -1 \end{bmatrix}\]
Exercise 4.4.9
Find the inverse of the matrix (if it exists): \[\begin{bmatrix} 2 & 1 & 3 \\ 4 & -1 & 0 \\ -7 & 2 & 1 \end{bmatrix}\]
Exercise 4.4.10
Find the inverse of the matrix (if it exists): \[\begin{bmatrix} 1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4 \end{bmatrix}\]
Exercise 4.4.11
Find the inverse of the matrix (if it exists): \[\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\alpha & \sin\alpha \\ 0 & \sin\alpha & -\cos\alpha \end{bmatrix}\]
Exercise 4.4.12
Let \(A = \begin{bmatrix} 3 & 7 \\ 2 & 5 \end{bmatrix}\) and \(B = \begin{bmatrix} 6 & 8 \\ 7 & 9 \end{bmatrix}\). Verify that \((AB)^{-1} = B^{-1}A^{-1}\).
Exercise 4.4.13
If \(A = \begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}\), show that \(A^2 - 5A + 7I = O\). Hence find \(A^{-1}\).
Exercise 4.4.14
For the matrix \(A = \begin{bmatrix} 3 & 2 \\ 1 & 1 \end{bmatrix}\), find the numbers \(a\) and \(b\) such that \(A^2 + aA + bI = O\).
Exercise 4.4.15
For the matrix \(A = \begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix}\), show that \(A^3 - 6A^2 + 5A + 11I = O\). Hence, find \(A^{-1}\).
Exercise 4.4.16
If \(A = \begin{bmatrix} 2 & -1 & 1 \\ -1 & 2 & -1 \\ 1 & -1 & 2 \end{bmatrix}\), verify that \(A^3 - 6A^2 + 9A - 4I = O\) and hence find \(A^{-1}\).
Exercise 4.4.17
Let A be a nonsingular square matrix of order \(3 \times 3\). Then \(|\text{adj } A|\) is equal to: (A) \(|A|\) (B) \(|A|^2\) (C) \(|A|^3\) (D) \(3|A|\)
Exercise 4.4.18
If A is an invertible matrix of order 2, then \(\det(A^{-1})\) is equal to: (A) \(\det(A)\) (B) \(\frac{1}{\det(A)}\) (C) 1 (D) 0
Exercise 4.5.1
Examine the consistency of the system of equations: \(x + 2y = 2\) \(2x + 3y = 3\)
Exercise 4.5.2
Examine the consistency of the system of equations: \(2x - y = 5\) \(x + y = 4\)
Exercise 4.5.3
Examine the consistency of the system of equations: \(x + 3y = 5\) \(2x + 6y = 8\)
Exercise 4.5.4
Examine the consistency of the system of equations: \(x + y + z = 1\) \(2x + 3y + 2z = 2\) \(ax + ay + 2az = 4\)
Exercise 4.5.5
Examine the consistency of the system of equations: \(3x - y - 2z = 2\) \(2y - z = -1\) \(3x - 5y = 3\)
Exercise 4.5.6
Examine the consistency of the system of equations: \(5x - y + 4z = 5\) \(2x + 3y + 5z = 2\) \(5x - 2y + 6z = -1\)
Exercise 4.5.7
Solve the system of linear equations using the matrix method: \(5x + 2y = 4\) \(7x + 3y = 5\)
Exercise 4.5.8
Solve the system of linear equations using the matrix method: \(2x - y = -2\) \(3x + 4y = 3\)
Exercise 4.5.9
Solve the system of linear equations using the matrix method: \(4x - 3y = 3\) \(3x - 5y = 7\)
Exercise 4.5.10
Solve the system of linear equations using the matrix method: \(5x + 2y = 3\) \(3x + 2y = 5\)
Exercise 4.5.11
Solve the system of linear equations using the matrix method: \(2x + y + z = 1\) \(x - 2y - z = \frac{3}{2}\) \(3y - 5z = 9\)
Exercise 4.5.12
Solve the system of linear equations using the matrix method: \(x - y + z = 4\) \(2x + y - 3z = 0\) \(x + y + z = 2\)
Exercise 4.5.13
Solve the system of linear equations using the matrix method: \(2x + 3y + 3z = 5\) \(x - 2y + z = -4\) \(3x - y - 2z = 3\)
Exercise 4.5.14
Solve the system of linear equations using the matrix method: \(x - y + 2z = 7\) \(3x + 4y - 5z = -5\) \(2x - y + 3z = 12\)
Exercise 4.5.15
If \(A = \begin{bmatrix} 2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2 \end{bmatrix}\), find \(A^{-1}\). Using \(A^{-1}\), solve the system of equations: \(2x - 3y + 5z = 11\) \(3x + 2y - 4z = -5\) \(x + y - 2z = -3\)
Exercise 4.5.16
The cost of 4 kg onion, 3 kg wheat, and 2 kg rice is ₹60. The cost of 2 kg onion, 4 kg wheat, and 6 kg rice is ₹90. The cost of 6 kg onion, 2 kg wheat, and 3 kg rice is ₹70. Find the cost of each item per kg by matrix method.
Exercise 4.11
Prove that the determinant is independent of \(\theta\): \[\begin{vmatrix} x & \sin\theta & \cos\theta \\ -\sin\theta & -x & 1 \\ \cos\theta & 1 & x \end{vmatrix}\]
Exercise 4.12
Evaluate: \[\begin{vmatrix} \cos\alpha \cos\beta & \cos\alpha \sin\beta & -\sin\alpha \\ -\sin\beta & \cos\beta & 0 \\ \sin\alpha \cos\beta & \sin\alpha \sin\beta & \cos\alpha \end{vmatrix}\]
Exercise 4.13
If \(A^{-1} = \begin{bmatrix} 3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2 \end{bmatrix}\) and \(B = \begin{bmatrix} 1 & 2 & -2 \\ -1 & 3 & 0 \\ 0 & -2 & 1 \end{bmatrix}\), find \((AB)^{-1}\).
Exercise 4.14
Let \(A = \begin{bmatrix} 1 & 2 & 1 \\ 2 & 3 & 1 \\ 1 & 1 & 5 \end{bmatrix}\). Verify that: (i) \([\text{adj } A]^{-1} = \text{adj}(A^{-1})\) (ii) \((A^{-1})^{-1} = A\)
Exercise 4.15
Evaluate: \[\begin{vmatrix} x & y & x+y \\ y & x+y & x \\ x+y & x & y \end{vmatrix}\]
Exercise 4.16
Evaluate: \[\begin{vmatrix} 1 & x & y \\ 1 & x+y & y \\ 1 & x & x+y \end{vmatrix}\]
Exercise 4.17
Solve the system of equations: \[\frac{2}{x} + \frac{3}{y} + \frac{10}{z} = 4\] \[\frac{4}{x} - \frac{6}{y} + \frac{5}{z} = 1\] \[\frac{6}{x} + \frac{9}{y} - \frac{20}{z} = 2\]
Exercise 4.18
If x, y, z are nonzero real numbers, then the inverse of matrix \(A = \begin{bmatrix} x & 0 & 0 \\ 0 & y & 0 \\ 0 & 0 & z \end{bmatrix}\) is: (A) \(\begin{bmatrix} x^{-1} & 0 & 0 \\ 0 & y^{-1} & 0 \\ 0 & 0 & z^{-1} \end{bmatrix}\) (B) \(xyz\begin{bmatrix} x^{-1} & 0 & 0 \\ 0 & y^{-1} & 0 \\ 0 & 0 & z^{-1} \end{bmatrix}\) (C) \(\frac{1}{xyz}\begin{bmatrix} x & 0 & 0 \\ 0 & y & 0 \\ 0 & 0 & z \end{bmatrix}\) (D) \(\frac{1}{xyz}\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\)
Exercise 4.19
Let \(A = \begin{bmatrix} 1 & \sin\theta & 1 \\ -\sin\theta & 1 & \sin\theta \\ -1 & -\sin\theta & 1 \end{bmatrix}\), where \(0 \le \theta \le 2\pi\). Then: (A) \(\det(A) = 0\) (B) \(\det(A) \in (2, \infty)\) (C) \(\det(A) \in (2, 4)\) (D) \(\det(A) \in [2, 4]\)