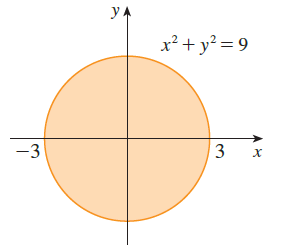Section 14.1: Functions of Several Variables
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 14.1: Functions of Several Variables |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 2:12 AM |
Table of contents
- Learning Outcomes
- Functions of 2 variables
- Domain: Definition and examples
- Graphs
- Practice graph plotting in softwares
- Level Curves and Surfaces
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Exercise 19
- Exercise 20
- Exercise 21
- Exercise 22
- Exercise 32
- Exercise 45
- Exercise 46
- Exercise 47
- Exercise 48
- Exercise 49
- Exercise 50
- Exercise 51
- Exercise 52
- Exercise 67
- Exercise 68
- Exercise 69
- Exercise 70
Learning Outcomes
In this section we will learn about
- Functions of 2 and 3 variables
- Grpahs
- Domains
- Level curves
- Level Surfaces
Functions of 2 variables
Definition
A function f of two variables is a rule that assigns to each ordered pair of real numbers \((x, y)\) in a set \(D\) a unique real number denoted by \(f(x, y)\). The set \(D\) is the domain of \(f\) and its range is the set of values that \(f\) takes on, that is, \(f(x, y) \mid (x, y) \in D\).
Example
- Volume of a cylinder \(V(r,h) = \pi r^2 h\)
- Area of rectangle \(A(l,b) = lb\)
Domain: Definition and examples
Definition
The domain of a function f is the collection of the points on which this function can be evaluated.
Example Question
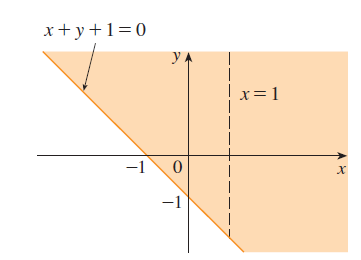
Find and sketch the domain of \[f(x,y) = \frac{\sqrt{x+y+1}}{x-1}\].
Example Question
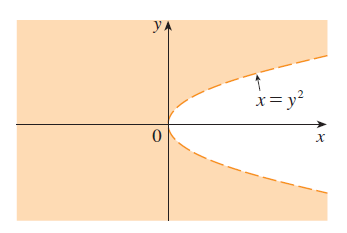
Find and sketch the domain of \(f(x, y) = x \ln(y^2 - x)\).
Example Question
Find and sketch the domain of \(g(x, y) = \sqrt{ 9 - x^2 - y^2}\).
Graphs
Definition If \(f\) is a function of two variables with domain \(D\), then the graph of \(f\) is the set of all points \((x, y, z)\) in \(\mathbb{R}^3\) such that \(z = f(x, y)\) and \((x, y) \in D\).
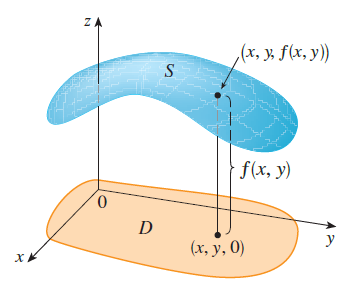
Example
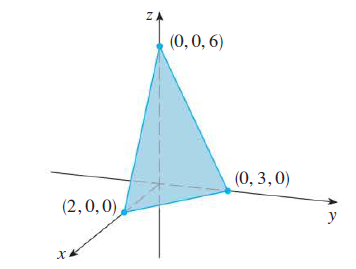
Sketch the graph of the function \(f(x, y) = 6 - 3x - 2y\).
Example
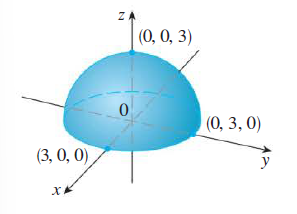
Sketch the graph of the function \(f(x, y) = \sqrt{9 - x^2 - y^2}\).
Practice graph plotting in softwares
Exercise
Plot graphs of these functions on Geobegra or any plotting software you like.
- \(f(x, y) = (x^2 + 3y^2) e^{-x^2 - y^2}\)
- \(f(x, y) = \sin x + \sin y\)
- \(f(x, y) = \frac{\sin x \sin y}{xy}\)
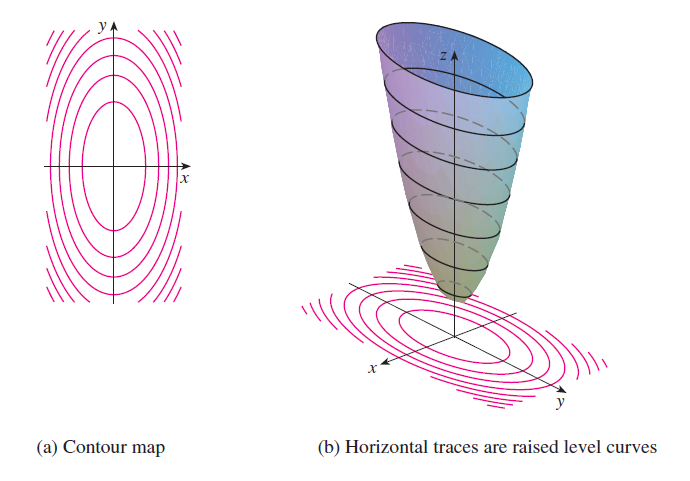
Level Curves and Surfaces
Definition
The level curves of a function \(f\) of two variables are the curves with
equations \(f(x, y) = k\), where \(k\) is a constant (in the range of \(f\)).
Example
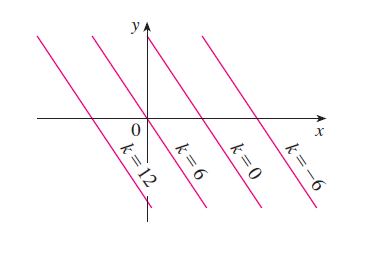
Sketch the level curves of the function \(f(x, y) = 6 - 3x - 2y\) for the values \(k = -6, 0, 6, 12\).
Example Level curves
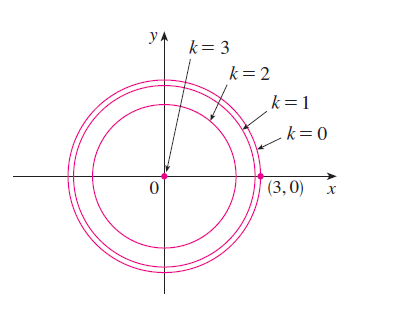
Sketch the level curves for the function \[ g(x,y) = \sqrt{ 9 - x^2 - y^2} \qquad \text{for} \qquad k = 0, 1, 2, 3. \]
Example Level Curves
Sketch some level curves for the function \[ h(x,y) = 4x^2 + y^2 + 1 \]
Exercise 1
In Example 2 we considered the function \(W
= f(T, v)\), where \(W\) is the
wind-chill index, \(T\) is the actual
temperature, and \(v\) is the wind
speed. A numerical representation is given in Table 1 on page 889.
(a) What is the value of \(f(-15,
40)\)? What is its meaning?
(b) Describe in words the meaning of the question “For what value of
\(v\) is \(f(-20, v) = -30\)?” Then answer the
question.
(c) Describe in words the meaning of the question “For what value of
\(T\) is \(f(T, 20) = -49\)?” Then answer the
question.
(d) What is the meaning of the function \(W =
f(-5, v)\)? Describe the behavior of this function.
(e) What is the meaning of the function \(W =
f(T, 50)\)? Describe the behavior of this function.
Exercise 2
The temperature-humidity index \(I\) (or humidex, for short) is the perceived air temperature when the actual temperature is \(T\) and the relative humidity is \(h\), so we can write \(I = f(T, h)\). The following table of values of \(I\) is an excerpt from a table compiled by the National Oceanic & Atmospheric Administration.
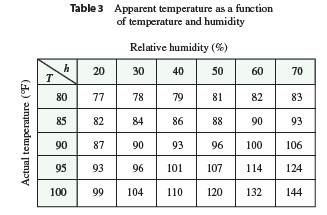
- What is the value of \(f(95, 70)\)?
What is its meaning?
- For what value of \(h\) is \(f(90, h) = 100\)?
- For what value of \(T\) is \(f(T, 50) = 88\)?
- What are the meanings of the functions \(I = f(80, h)\) and \(I = f(100, h)\)? Compare the behavior of these two functions of \(h\).
Exercise 3
A manufacturer has modeled its yearly production function \(P\) (the monetary value of its entire
production in millions of dollars) as a Cobb-Douglas function
\[P(L, K) =
1.47L^{0.65}K^{0.35}\]
where \(L\) is the number of labor
hours (in thousands) and \(K\) is the
invested capital (in millions of dollars). Find \(P(120, 20)\) and interpret it.
Exercise 4
Verify for the Cobb-Douglas production function
\[P(L, K) =
1.01L^{0.75}K^{0.25}\]
discussed in Example 3 that the production will be doubled if both the
amount of labor and the amount of capital are doubled. Determine whether
this is also true for the general production function
\[P(L, K) = bL^rK^{1 - r}\]
Exercise 5
A model for the surface area of a human body is given by the
function
\[S = f(w, h) =
0.1091w^{0.425}h^{0.725}\]
where \(w\) is the weight (in pounds),
\(h\) is the height (in inches), and
\(S\) is measured in square feet.
(a) Find \(f(160, 70)\) and interpret
it.
(b) What is your own surface area?
Exercise 6
The wind-chill index \(W\) discussed
in Example 2 has been modeled by the following function:
\[W(T, v) = 13.12 + 0.6215T - 11.37v^{0.16} +
0.3965Tv^{0.16}\]
Check to see how closely this model agrees with the values in Table 1
for a few values of \(T\) and \(v\).
Exercise 7
The wave heights \(h\) in the open
sea depend on the speed \(v\) of the
wind and the length of time \(t\) that
the wind has been blowing at that speed. Values of the function \(h = f(v, t)\) are recorded in feet in Table
4.
(a) What is the value of \(f(40, 15)\)?
What is its meaning?
(b) What is the meaning of the function \(h =
f(30, t)\)? Describe the behavior of this function.
(c) What is the meaning of the function \(h =
f(v, 30)\)? Describe the behavior of this function.
Exercise 9
Let \(g(x, y) = \cos(x +
2y)\).
(a) Evaluate \(g(2, -1)\).
(b) Find the domain of \(g\).
(c) Find the range of \(g\).
Exercise 10
Let \(F(x, y) = 1 + \sqrt{4 -
y^2}\).
(a) Evaluate \(F(3, 1)\).
(b) Find and sketch the domain of \(F\).
(c) Find the range of \(F\).
Exercise 11
Let \(f(x, y, z) = \sqrt{x} + \sqrt{y} +
\sqrt{z} + \ln(4 - x^2 - y^2 - z^2)\).
(a) Evaluate \(f(1, 1, 1)\).
(b) Find and describe the domain of \(f\).
Exercise 12
Let \(g(x, y, z) = x^3y^2\sqrt{10 - x - y -
z}\).
(a) Evaluate \(g(1, 2, 3)\).
(b) Find and describe the domain of \(g\).
Exercise 13
Find and sketch the domain of the function.
\(f(x, y) = \sqrt{x - 2} + \sqrt{y -
1}\)
Exercise 14
Find and sketch the domain of the function.
\(f(x, y) = \sqrt[4]{x - 3y}\)
Exercise 15
Find and sketch the domain of the function.
\(f(x, y) = \ln(9 - x^2 - 9y^2)\)
Exercise 16
Find and sketch the domain of the function.
\(f(x, y) = \frac{\sqrt{x^2 + y^2 - 4}}{1 -
x^2 - y^2}\)
Exercise 17
Find and sketch the domain of the function.
\(g(x, y) = \frac{x - y}{x + y}\)
Exercise 18
Find and sketch the domain of the function.
\(g(x, y) = \frac{\ln(2 - x)}{1 - x^2 -
y^2}\)
Exercise 19
Find and sketch the domain of the function.
\(f(x, y) = \frac{\sqrt{y - x^2}}{1 -
x^2}\)
Exercise 20
Find and sketch the domain of the function.
\(f(x, y) = \sin^{-1}(x + y)\)
Exercise 21
Find and sketch the domain of the function.
\(f(x, y, z) = \sqrt{4 - x^2} + \sqrt{9 - y^2}
+ \sqrt{1 - z^2}\)
Exercise 22
Find and sketch the domain of the function.
\(f(x, y, z) = \ln(16 - 4x^2 - 4y^2 -
z^2)\)
Exercise 32
Match the function with its graph (labeled I–VI). Give reasons for
your choices.
(a) \(f(x, y) = \frac{1}{1 + x^2 +
y^2}\)
(b) \(f(x, y) = \frac{1}{1 +
x^2y^2}\)
(c) \(f(x, y) = \ln(x^2 + y^2)\)
(d) \(f(x, y) = \cos\sqrt{x^2 +
y^2}\)
(e) \(f(x, y) = |xy|\)
(f) \(f(x, y) = \cos(xy)\)
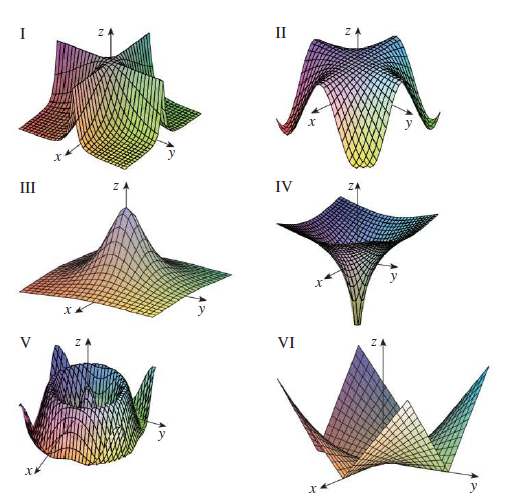
Exercise 45
Draw a contour map of the function showing several level
curves.
\(f(x, y) = x^2 - y^2\)
Exercise 46
Draw a contour map of the function showing several level
curves.
\(f(x, y) = xy\)
Exercise 47
Draw a contour map of the function showing several level
curves.
\(f(x, y) = \sqrt{x} + y\)
Exercise 48
Draw a contour map of the function showing several level
curves.
\(f(x, y) = \ln(x^2 + 4y^2)\)
Exercise 49
Draw a contour map of the function showing several level
curves.
\(f(x, y) = ye^x\)
Exercise 50
Draw a contour map of the function showing several level
curves.
\(f(x, y) = y - \arctan{x}\)
Exercise 51
Draw a contour map of the function showing several level
curves.
\(f(x, y) = \sqrt[3]{x^2 + y^2}\)
Exercise 52
Draw a contour map of the function showing several level
curves.
\(f(x, y) = \frac{y}{x^2 + y^2}\)
Exercise 67
Describe the level surfaces of the function.
\(f(x, y, z) = x + 3y + 5z\)
Exercise 68
Describe the level surfaces of the function.
\(f(x, y, z) = x^2 + 3y^2 + 5z^2\)
Exercise 69
Describe the level surfaces of the function.
\(f(x, y, z) = y^2 + z^2\)
Exercise 70
Describe the level surfaces of the function.
\(f(x, y, z) = x^2 - y^2 - z^2\)