Section 14.2: Limits and Continuity
| Site: | Freebirds Moodle |
| Course: | Mathematical Methods I - SNIOE - Monsoon 2025 |
| Book: | Section 14.2: Limits and Continuity |
| Printed by: | Guest user |
| Date: | Friday, 26 December 2025, 2:12 AM |
Learning Outcomes
In this section we will learn about
- Limits and Continuity of 2 and 3 variable functions
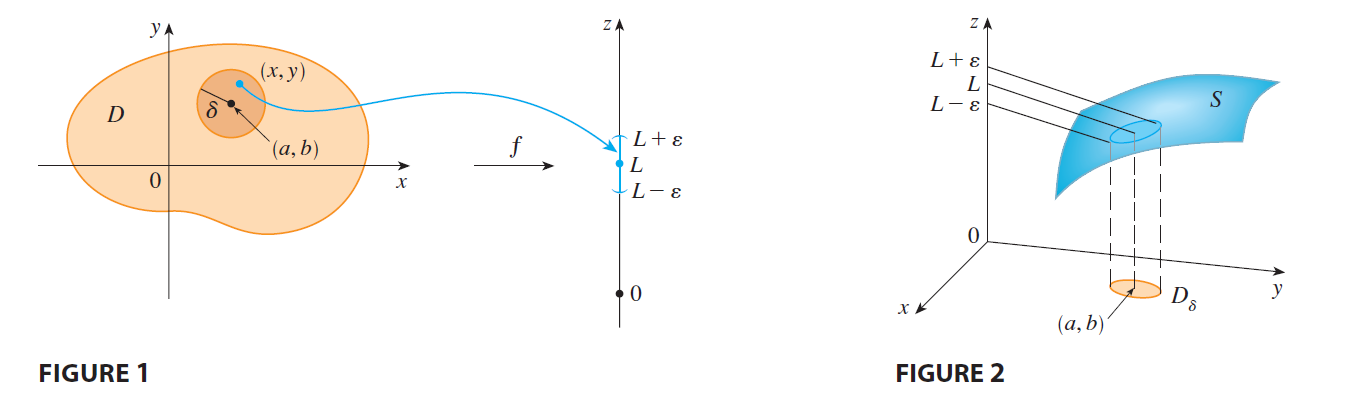
Definition of Limit
Definition
Let \(f\) be a function of two
variables whose domain \(D\) includes
points arbitrarily close to \((a, b)\).
Then we say that the limit of \(f(x,
y)\) as \((x, y)\) approaches
\((a, b)\) is \(L\) and we write:
\[ \lim_{(x, y) \to (a, b)} f(x, y) = L \]
if for every number \(\varepsilon > 0\) there is a corresponding number \(\delta > 0\) such that
\[ \text{if } (x, y) \in D \quad \text{and} \quad 0 < \sqrt{(x - a)^2 + (y - b)^2} < \delta \quad \text{then} \quad |f(x, y) - L| < \varepsilon \]
Simple Interpretation Function \(f(x,y)\) value approaches \(L\) regardless of the path through which \((x,y)\) approaces \((a,b)\).
Limit Does not Exist if Find two paths along which function values approaches different limit.
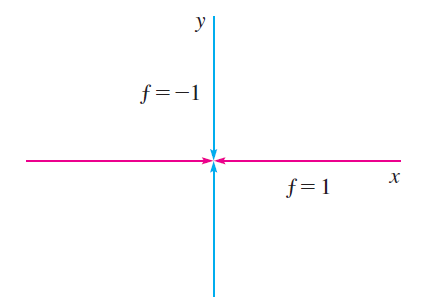
Example 1: Limit does not exist
Example
Show that \(\lim_{(x, y) \to (0, 0)} \frac{x^2
- y^2}{x^2 + y^2}\) does not exist.
Example 2: Limit does not exist
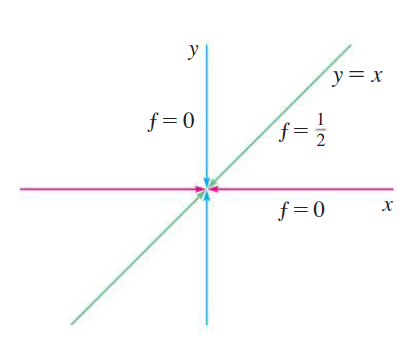
Example
Show that \(\lim_{(x, y) \to (0, 0)}
\frac{xy}{x^2 + y^2}\) does not exist.
Example 2: Limit does not exist
Example
Show that \(\lim_{(x, y) \to (0, 0)}
\frac{xy^2}{x^2 + y^4}\) does not exist.
Example 2: Limit exist
Example
Show that \(\lim_{(x, y) \to (0, 0)}
\frac{x^2y}{x^2 + y^2}\) exists.
Note Detailed proof is not in the syllabus. Just plot the graph. See that it is pretty smooth at \((0,0)\).
Definition: Continuity
Definition
A function \(f\) of two variables is
called continuous at \((a,
b)\) if
\[ \lim_{(x, y) \to (a, b)} f(x, y) = f(a, b) \]
We say \(f\) is continuous on \(D\) if \(f\) is continuous at every point \((a, b)\) in \(D\).
Note In this course you will not be asked to prove continuity. Use these rules.
- Polynomials are always continuous
- Most forumulas as continuous if you can evaluate the formula at the given point.
Example
Evaluate
\[
\lim_{(x, y) \to (1, 2)} \left(x^2 y^3 - x^3 y^2 + 3x + 2y\right).
\]
Solution
Since \(f(x, y) = x^2 y^3 - x^3 y^2 + 3x +
2y\) is a polynomial, it is continuous everywhere, so we can find
the limit by direct substitution:
\[ \lim_{(x, y) \to (1, 2)} \left(x^2 y^3 - x^3 y^2 + 3x + 2y\right) = 1^2 \cdot 2^3 - 1^3 \cdot 2^2 + 3 \cdot 1 + 2 \cdot 2 = 11 \]
Example
Where is the function
\[
f(x, y) = \frac{x^2 - y^2}{x^2 + y^2}
\]
continuous?
Solution
The function \(f\) is discontinuous at
\((0, 0)\) because it is not defined
there. Since \(f\) is a rational
function, it is continuous on its domain, which is the set
\[
D = \{(x, y) \mid (x, y) \neq (0, 0)\}.
\]