Section 1.1 & 1.2: Types of Relations
Example Exercise
Example 1
Let \(A\) be the set of all students of
a boys school. Show that the relation \(R\) in \(A\) given by:
\[ R = \{(a, b) : a \text{ is sister of } b\} \]
is the empty relation and
\[ R' = \{(a, b) : \text{the difference between heights of } a \text{ and } b \text{ is less than } 3 \text{ meters}\} \]
is the universal relation.
Equivalence Relation
One of the most important relation, which plays a significant role in Mathematics, is an equivalence relation. To study equivalence relation, we first consider three types of relations, namely reflexive, symmetric and transitive.
Definition A relation \(R\) in a set \(A\) is called
(i) reflexive, if \((a, a) \in
R\), for every \(a \in
A\),
(ii) symmetric, if \((a_1, a_2) \in
R\) implies that \((a_2, a_1) \in
R\), for all \(a_1, a_2 \in
A\),
(iii) transitive, if \((a_1, a_2) \in
R\) and \((a_2, a_3) \in R\)
implies that \((a_1, a_3) \in R\), for
all \(a_1, a_2, a_3 \in A\).
Definition
A relation \(R\) in a set \(A\) is said to be an equivalence
relation if \(R\) is reflexive,
symmetric and transitive.
Example
Let \(T\) be the set of all triangles
in a plane with \(R\) a relation in
\(T\) given by
\[
R = \{(T_1, T_2) : T_1 \text{ is congruent to } T_2\}.
\]
Show that \(R\) is an equivalence
relation.
Example
Let \(L\) be the set of all lines in a
plane and \(R\) be the relation in
\(L\) defined as
\[
R = \{(L_1, L_2) : L_1 \text{ is perpendicular to } L_2\}.
\]
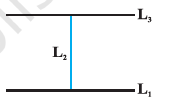
Show that \(R\) is symmetric but neither reflexive nor transitive.
Example
Show that the relation \(R\) in the set
\(\{1, 2, 3\}\) given by
\[
R = \{(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)\}
\]
is reflexive but neither symmetric nor transitive.
