Shape transformation map
More generally, we consider a change of variables that is given by a transformation T from the uv-plane to the xy-plane: \[ T(u, v) = (x, y) \] where x and y are related to u and v by the equations
\[ x = g(u, v) \qquad y = h(u, v) \tag{3} \]
or, as we sometimes write, \[ x = x(u, v) \qquad y = y(u, v) \] We usually assume that T is a \(C^1\) transformation, which means that g and h have continuous first-order partial derivatives.
A transformation T is really just a function whose domain and range are both subsets of \(\mathbb{R}^2\). If \(T(u_1, v_1) = (x_1, y_1)\), then the point \((x_1, y_1)\) is called the image of the point \((u_1, v_1)\). If no two points have the same image, T is called one-to-one.
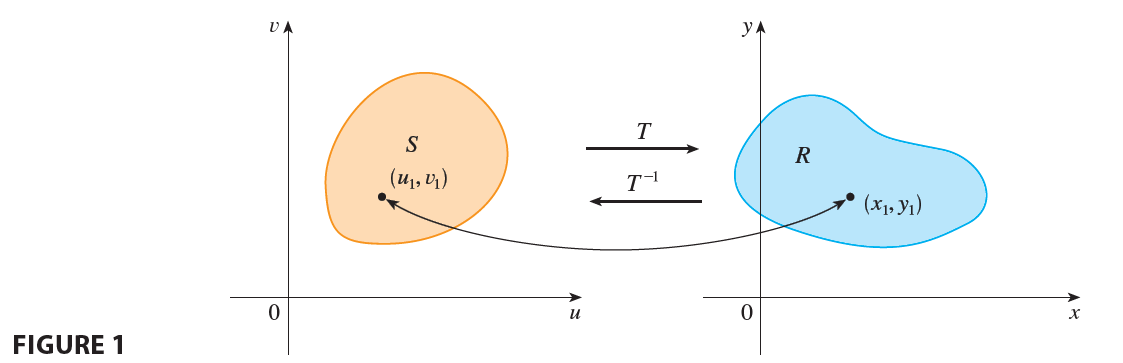
Figure 1 shows the effect of a transformation T on a region S in the uv-plane. T transforms S into a region R in the xy-plane called the image of S, consisting of the images of all points in S.
If T is a one-to-one transformation, then it has an inverse transformation \(T^{-1}\) from the xy-plane to the uv-plane and it may be possible to solve Equations 3 for u and v in terms of x and y: \[ u = G(x, y) \qquad v = H(x, y) \]
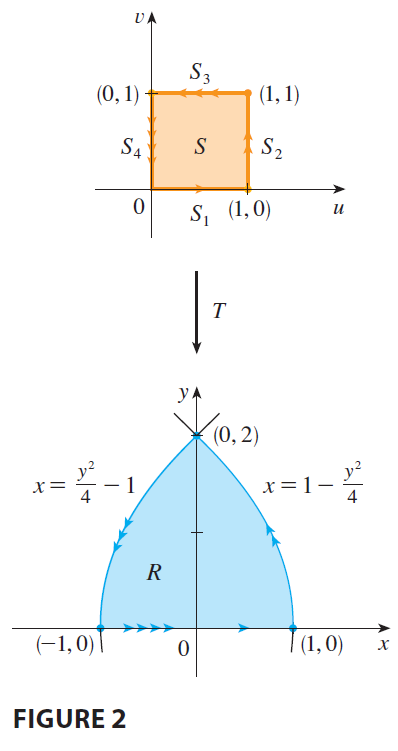
EXAMPLE 1 A transformation is defined by the equations \[ x = u^2 - v^2 \qquad y = 2uv \] Find the image of the square \(S = \{(u, v) | 0 \le u \le 1, 0 \le v \le 1\}\).