Exercise 4

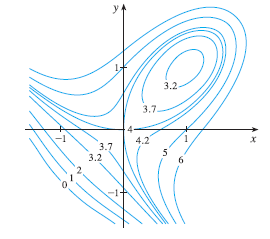
Use the level curves in the figure to predict the location of the critical points of \(f(x, y) = 3x - x^3 - 2y^2 + y^4\) and whether f has a saddle point or a local maximum or minimum at each critical point. Explain your reasoning. Then use the Second Derivatives Test to confirm your predictions.