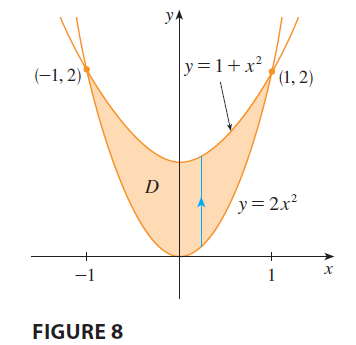
SOLUTION The parabolas intersect when \(2x^2 = 1 + x^2\), that is, \(x^2 = 1\), so \(x
= \pm 1\). We note that the region \(D\), sketched in Figure 8, is a type I
region but not a type II region and we can write \[
D = \{(x, y) | -1 \le x \le 1, 2x^2 \le y \le 1 + x^2\}
\] Since the lower boundary is \(y =
2x^2\) and the upper boundary is \(y =
1 + x^2\), Equation 3 gives \[
\iint_D (x + 2y) dA = \int_{-1}^1 \int_{2x^2}^{1+x^2} (x + 2y) dy dx
\] \[
= \int_{-1}^1 [xy + y^2]_{y=2x^2}^{y=1+x^2} dx
\] \[
= \int_{-1}^1 [x(1+x^2) + (1+x^2)^2 - x(2x^2) - (2x^2)^2] dx
\] \[
= \int_{-1}^1 (-3x^4 - x^3 + 2x^2 + x + 1) dx
\] \[
= \left[ -3\frac{x^5}{5} - \frac{x^4}{4} + 2\frac{x^3}{3} +
\frac{x^2}{2} + x \right]_{-1}^1 = \frac{32}{15}
\]
NOTE When we set up a double integral as in Example
1, it is essential to draw a diagram. Often it is helpful to draw a
vertical arrow as in Figure 8. Then the limits of integration for the
inner integral can be read from the diagram as follows: The arrow starts
at the lower boundary \(y = g_1(x)\),
which gives the lower limit in the integral, and the arrow ends at the
upper boundary \(y = g_2(x)\), which
gives the upper limit of integration. For a type II region the arrow is
drawn horizontally from the left boundary to the right boundary.