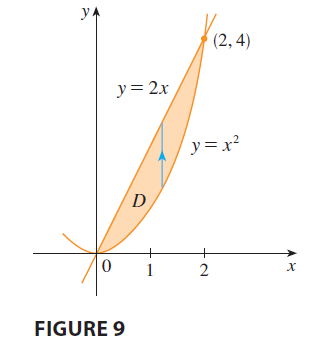
SOLUTION 1 From Figure 9 we see that \(D\) is a type I region and \[
D = \{(x, y) | 0 \le x \le 2, x^2 \le y \le 2x\}
\] Therefore the volume under \(z = x^2
+ y^2\) and above \(D\) is \[
V = \iint_D (x^2 + y^2) dA = \int_0^2 \int_{x^2}^{2x} (x^2 + y^2) dy dx
\] \[
= \int_0^2 \left[ x^2y + \frac{y^3}{3} \right]_{y=x^2}^{y=2x} dx =
\int_0^2 \left[ x^2(2x) + \frac{(2x)^3}{3} - x^2(x^2) -
\frac{(x^2)^3}{3} \right] dx
\] \[
= \int_0^2 \left( 2x^3 + \frac{8x^3}{3} - x^4 - \frac{x^6}{3} \right) dx
= \int_0^2 \left( \frac{14x^3}{3} - x^4 - \frac{x^6}{3} \right) dx
\] \[
= \left[ \frac{14}{3}\frac{x^4}{4} - \frac{x^5}{5} - \frac{x^7}{21}
\right]_0^2 = \frac{7(16)}{6} - \frac{32}{5} - \frac{128}{21} =
\frac{216}{35}
\]
SOLUTION 2 From Figure 11 we see that \(D\) can also be written as a type II
region: \[
D = \{(x, y) | 0 \le y \le 4, \frac{y}{2} \le x \le \sqrt{y}\}
\] Therefore another expression for \(V\) is \[
V = \iint_D (x^2 + y^2) dA = \int_0^4 \int_{y/2}^{\sqrt{y}} (x^2 + y^2)
dx dy
\] \[
= \int_0^4 \left[ \frac{x^3}{3} + y^2x \right]_{x=y/2}^{x=\sqrt{y}} dy =
\int_0^4 \left( \frac{y^{3/2}}{3} + y^{5/2} - \frac{y^3}{24} -
\frac{y^3}{2} \right) dy
\] \[
= \int_0^4 \left( \frac{y^{3/2}}{3} + y^{5/2} - \frac{13y^3}{24} \right)
dy = \left[ \frac{2y^{5/2}}{15} + \frac{2y^{7/2}}{7} - \frac{13y^4}{96}
\right]_0^4 = \frac{216}{35}
\]