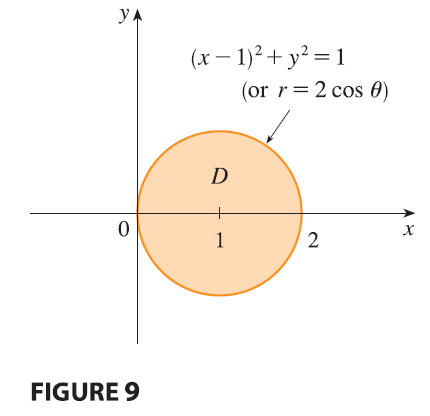
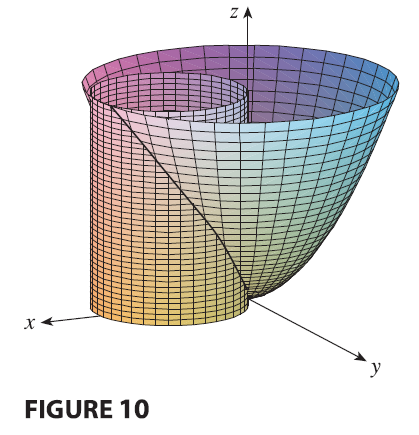
SOLUTION The solid lies above the disk \(D\) whose boundary circle has equation
\(x^2 + y^2 = 2x\) or, after completing
the square, \[
(x - 1)^2 + y^2 = 1
\] In polar coordinates we have \(x^2 +
y^2 = r^2\) and \(x = r \cos
\theta\), so the boundary circle becomes \(r^2 = 2r \cos \theta\), or \(r = 2 \cos \theta\). Thus the disk \(D\) is given by \[
D = \{(r, \theta) | -\pi/2 \le \theta \le \pi/2, 0 \le r \le 2 \cos
\theta\}
\] and, by Formula 3, we have \[
V = \iint_D (x^2 + y^2) dA = \int_{-\pi/2}^{\pi/2} \int_0^{2 \cos
\theta} r^2 r dr d\theta = \int_{-\pi/2}^{\pi/2} \left[ \frac{r^4}{4}
\right]_0^{2 \cos \theta} d\theta
\] \[
= \int_{-\pi/2}^{\pi/2} 4 \cos^4 \theta d\theta = 8 \int_0^{\pi/2}
\cos^4 \theta d\theta = 8 \int_0^{\pi/2} \left( \frac{1 + \cos
2\theta}{2} \right)^2 d\theta
\] \[
= 2 \int_0^{\pi/2} [1 + 2 \cos 2\theta + \cos^2 2\theta] d\theta = 2
\int_0^{\pi/2} \left[ 1 + 2 \cos 2\theta + \frac{1}{2}(1 + \cos 4\theta)
\right] d\theta
\] \[
= 2 \left[ \frac{3}{2}\theta + \sin 2\theta + \frac{1}{8}\sin 4\theta
\right]_0^{\pi/2} = 2\left(\frac{3}{2}\right)\left(\frac{\pi}{2}\right)
= \frac{3\pi}{2}
\]