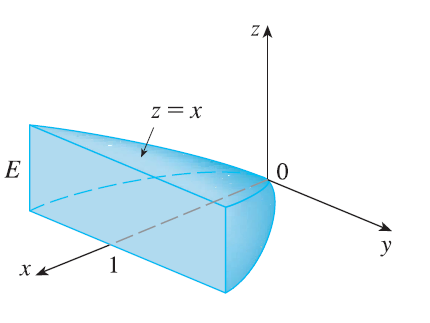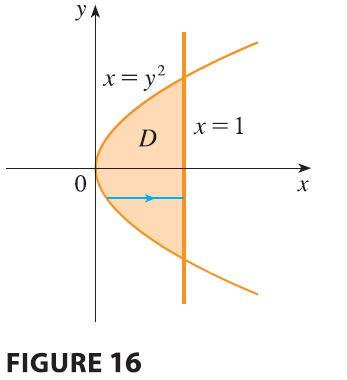
SOLUTION The solid \(E\) and its projection onto the \(xy\)-plane are shown in Figure 16. The
lower and upper surfaces of \(E\) are
the planes \(z = 0\) and \(z = x\), so we describe \(E\) as a type 1 region: \[
E = \{(x, y, z) | -1 \le y \le 1, y^2 \le x \le 1, 0 \le z \le x\}
\] Then, if the density is \(\rho(x, y,
z) = \rho\), the mass is \[
m = \iiint_E \rho dV = \int_{-1}^1 \int_{y^2}^1 \int_0^x \rho dz dx dy =
\rho \int_{-1}^1 \int_{y^2}^1 x dx dy
\] \[
= \rho \int_{-1}^1 \left[ \frac{x^2}{2} \right]_{x=y^2}^{x=1} dy =
\frac{\rho}{2} \int_{-1}^1 (1 - y^4) dy = \rho \int_0^1 (1 - y^4) dy =
\rho \left[ y - \frac{y^5}{5} \right]_0^1 = \frac{4\rho}{5}
\] Because of the symmetry of \(E\) and \(\rho\) about the \(xz\)-plane, we can immediately say that
\(M_{xz} = 0\) and therefore \(\bar{y} = 0\). The other moments are \[
M_{yz} = \iiint_E x\rho dV = \int_{-1}^1 \int_{y^2}^1 \int_0^x x\rho dz
dx dy = \rho \int_{-1}^1 \int_{y^2}^1 x^2 dx dy
\] \[
= \rho \int_{-1}^1 \left[ \frac{x^3}{3} \right]_{x=y^2}^{x=1} dy =
\frac{2\rho}{3} \int_0^1 (1 - y^6) dy = \frac{2\rho}{3} \left[ y -
\frac{y^7}{7} \right]_0^1 = \frac{4\rho}{7}
\] \[
M_{xy} = \iiint_E z\rho dV = \int_{-1}^1 \int_{y^2}^1 \int_0^x z\rho dz
dx dy = \rho \int_{-1}^1 \int_{y^2}^1 \left[ \frac{z^2}{2}
\right]_{z=0}^{z=x} dx dy
\] \[
= \frac{\rho}{2} \int_{-1}^1 \int_{y^2}^1 x^2 dx dy = \frac{\rho}{2}
\frac{4}{7} = \frac{2\rho}{7}
\] Therefore the center of mass is \[
(\bar{x}, \bar{y}, \bar{z}) = \left( \frac{M_{yz}}{m}, \frac{M_{xz}}{m},
\frac{M_{xy}}{m} \right) = \left( \frac{4\rho/7}{4\rho/5}, 0,
\frac{2\rho/7}{4\rho/5} \right) = \left( \frac{5}{7}, 0, \frac{5}{14}
\right)
\]