Section 1.3: Functions
Types of Functions
Consider the functions \(f_1, f_2, f_3\) and \(f_4\) given by the following diagrams.
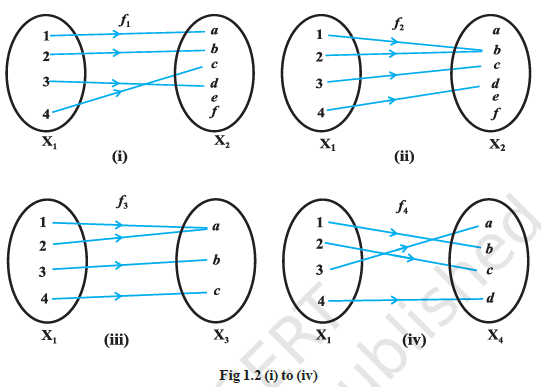
In Fig 1.2, we observe that the images of distinct elements of \(X_1\) under the function \(f_1\) are distinct, but the image of two distinct elements 1 and 2 of \(X_1\) under \(f_1\) is same, namely \(b\). Further, there are some elements like \(e\) and \(f\) in \(X_2\) which are not images of any element of \(X_1\) under \(f_1\), while all elements of \(X_3\) are images of some elements of \(X_1\) under \(f_3\). The above observations lead to the following definitions:
Definition: Injdective Functions or One-One
Functions
A function \(f : X \to Y\) is defined
to be one-one (or injective), if the
images of distinct elements of \(X\)
under \(f\) are distinct, i.e. for
every \(x_1, x_2 \in X\), \(f(x_1) = f(x_2)\) implies \(x_1 = x_2\). Otherwise, \(f\) is called many-one.
The functions \(f_1\) and \(f_4\) in Fig 1.2 (i) and (iv) are one-one and the function \(f_2\) and \(f_3\) in Fig 1.2 (ii) and (iii) are many-one.
Definition: Onto Functions or Surjective
Functions
A function \(f : X \to Y\) is said to
be onto (or surjective), if every
element of \(Y\) is the image of some
element of \(X\) under \(f\), i.e., for every \(y \in Y\), there exists an element \(x\) in \(X\) such that \(f(x) = y\).
The function \(f_3\) and \(f_4\) in Fig 1.2 (iii), (iv) are onto and the function \(f_1\) in Fig 1.2 (i) is not onto as elements \(e, f\) in \(X_2\) are not the image of any element in \(X_1\) under \(f_1\).
Remark
\(f : X \to Y\) is onto if and only if
\(\text{Range of } f = Y\).
Definition: Bijective functions
A function \(f : X \to Y\) is said to
be one-one and onto (or bijective), if \(f\) is both one-one and onto.
The function \(f_4\) in Fig 1.2 (iv) is one-one and onto.
